6.3. Оптимальные алгоритмы приема при полностью известных сигналах (когерентный прием)

Предположим, что все искажения в канале строго детерминированы и случайным является только гауссовский аддитивный шум n(t), который вначале полагаем белым, со спектральной плотностью N₀. Это значит, что при передаче сигнала u_i(t) (символа b_i (i = 0,1,...,m-1) приходящий сигнал можно описать моделью (3.38):

где все s_i(t) = ku_i(t-τ) (i = 0, 1,..., m-1) известны. Неизвестны лишь реализация помехи и индекс i действительно переданного сигнала, который и должна определить решающая схема.

Будем также считать, что все s_i(t) являются финитными сигналами, длительность которых Т. Это имеет место, если передаваемые сигналы u_i(t) финитны и имеют одинаковую длительность (система синхронная), а в канале нет ни многолучевого распространения, ни линейных искажений, вызывающих увеличение длительности сигнала (либо они скорректированы).

В дальнейшем будем везде полагать, что в системе обеспечена надежная тактовая синхронизация, т. е. границы тактового интервала, на котором приходит сигнал s(t), известны точно. Вопросы синхронизации весьма существенны при реализации оптимальных демодуляторов и синхронных систем связи вообще, но они выходят за пределы данного курса. Момент начала посылки s(t) примем за нуль.

Определим в этих условиях алгоритм работы оптимального (т. е. основанного на правиле максимального правдоподобия) демодулятора, анализирующего сигнал на тактовом интервале 0-Т. Для этого необходимо найти отношения правдоподобия для всех m возможных сигналов относительно нулевой гипотезы (s(t)=0; z(t) = n(t)).

Задача затрудняется тем, что ширина спектра сигнала бесконечна (поскольку он финитный), а поэтому пространство сигналов бесконечномерное L₂(Т). Для таких сигналов (или бесконечномерных векторов), как отмечалось, не существует плотности вероятностей. Однако существуют "-мерные плотности вероятностей для любых n сечений сигнала (см. § 2.1).

Заменим вначале белый шум квазибелым, имеющим ту же одностороннюю спектральную плотность мощности N₀, но только в некоторой полосе частот F = n/2T, где n>>1. Рассмотрим вначале дополнительную гипотезу, т. е. будем считать что Z(t) - шум. Возьмем на тактовом интервале n равноотстоящих сечений через Δt = 1/2F = T/n. Отсчеты Z₁,...., Z_n в этих сечениях для квазибелого гауссовского шума независимы в соответствии с (2.49). Поэтому n-мерная плотность вероятностей для взятых отсчетов

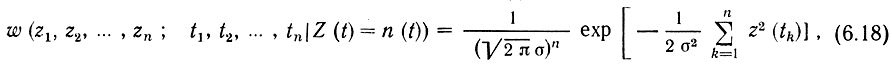
где σ² = N₀F - дисперсия (мощность) квазибелого шума.

При гипотезе, что передавался символ b_i, согласно (6.17) n(t) = z(t) - s_i(t). Следовательно, условная n-мерная плотность вероятности сечений Z(t) определится такой же формулой, как и (6.18), если z(t_k) заменить разностью z(t_k)-s_i(t_k), представляющей при этой гипотезе шум:

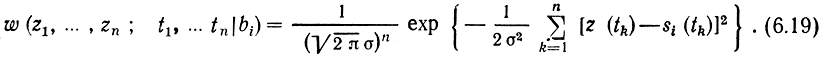
Отношение правдоподобия для сигнала s_i (относительно дополнительной гипотезы), вычисленное для n сечений:

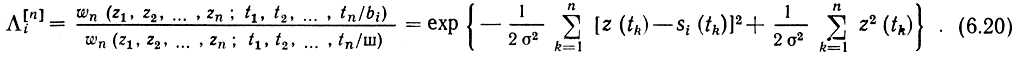
Заменим дисперсию σ² ее выражением: σ² = N₀F = N₀/(2Δt). Тогда

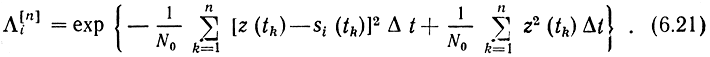
По правилу максимума правдоподобия в случае квазибелого шума решающая схема должна выбирать значение i, обеспечивающее максимум Λ_i^[n]. Вместо максимума Λ_i можно отыскивать максимум его логарифма:

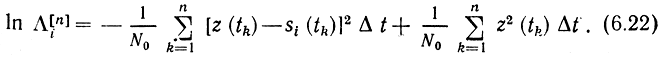
Второй член в (6.22) не зависит от t и его можно при сравнении гипотез не учитывать. Тогда правило решения о том, что передавался символ b_i, согласно (6.10) можно выразить системой неравенств

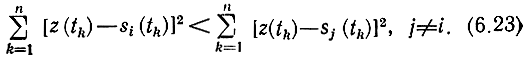
Вернемся теперь к исходной задаче для белого шума. Для этого будем расширять полосу F, тогда число сечений п стремится к бесконечности, а Δt - к нулю. Суммы в (6.22) обратятся в интегралы, и травило решения определится так:

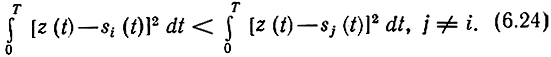
Выражение (6.24) определяет те операции (алгоритм работы), которые должен совершать оптимальный приемник над входным колебанием z(t).

На рис. 6.2 для m = 2 показана структурная схема приемного устройства, работающего в соответствии с алгоритмом (6.24).

Здесь "-" - вычитающие устройства; Γ₀, Γ₁ - генераторы опорных сигналов s₀(t), s₁(t); "KB" - квадраторы; ∫ - интеграторы; РУ - решающее устройство, определяющее в моменты времени, кратные Т (при замыкании ключей), номер ветви с минимальным сигналом.

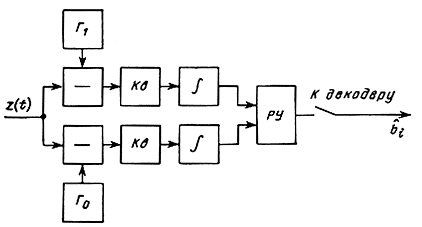
Рис. 6.2. Структурная схема оптимального приемного устройства при точно известных сигналах с квадраторами

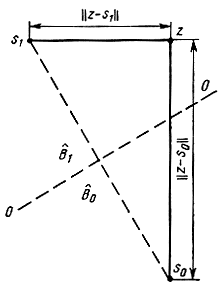
Рис. 6.3. Оптимальное разбиение пространства принимаемых колебаний при двоичном коде и точно известных сигналов

При m>2 в схеме рис. 6.2 и других нижеприведенных схемах растет соответственно число ветвей обработки сигнала, попадающих на РУ.

В пространстве Гильберта

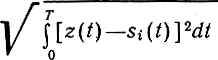
определяет норму разности векторов z и s или расстояние между ними^*. Поэтому алгоритм (6.24) можно записать в виде

и придать ему простую геометрическую интерпретацию: оптимальный демодулятор должен регистрировать тот из сигналов s_i(t) (соответствующий символу b_i), который "ближе" к принятому колебанию z(t). В качестве примера на рис. 6.3 показано оптимальное разбиение двумерного пространства принимаемых сигналов z(t) при передаче сигналов s₁(t) и s₀(t). Области принятия решения в пользу символов 0 или 1 расположены по обе стороны от прямой 0-0, перпендикулярной отрезку, соединяющему точки сигналов и делящих его пополам.

Наличие в схеме рис. 6.2 квадраторов, призванных обеспечить квадратичное преобразование мгновенных значений входных сигналов во всем их динамическом диапазоне, часто затрудняет ее реализацию. Поэтому на основе (6.24) получим эквивалентный алгоритм приема, не требующий устройств возведения в квадрат.

Раскрыв скобки под знаком интеграла и сократив в обеих частях неравенств (6.24) слагаемое

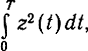
приходим к алгоритму приема:

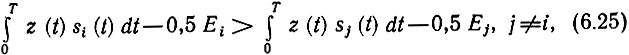
где E_j - энергия ожидаемого сигнала s_j(t) :

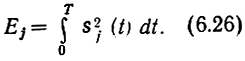
Для двоичной системы алгоритм (6.25) сводится к проверке одного неравенства

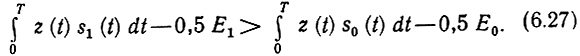
Устройство, непосредственно вычисляющее скалярное произведение

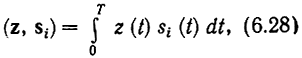
называют активным фильтром, или коррелятором, поэтому приемник, реализующий алгоритм (6.25), называют корреляционным.

^* (Для n-мерного пространства Евклида эта норма равна )

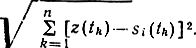
На рис. 6.4 показана структурная схема приемного устройства, работающего в соответствии с (6.27). Здесь блоки × - перемножители; Γ₀, Γ₁ - генераторы опорных сигналов s₀(t) s₁(t); ∫ - интеграторы; "-" - вычитающие устройства; РУ - решающее устройство, определяющее в моменты времени, кратные Т (при замыкании ключа), i = 0, 1 - номер ветви с максимальным сигналом.

Если сигналы u_i(t) выбраны таким образом, что все их реализации (а следовательно, и все реализации s_i(t) имеют одинаковые энергии (E_i = const), алгоритм приема (6.25) (и соответственно его реализация) упрощается (отпадает необходимость в вычитающих устройствах) и принимает вид

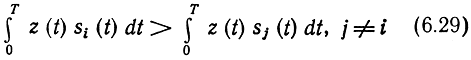
или

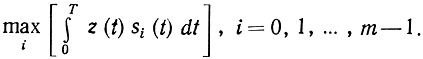
Из (6.29) видно, что правило решения не изменится, если сигнал z(t), поступающий на вход демодулятора, умножить на любое число. Поэтому система, в которой все реализации сигнала имеют равную энергию, отличается тем, что оптимальный алгоритм приема в ней не требует знания "масштаба" приходящего сигнала или, другими словами, знания коэффициента передачи k канала. Эта важная особенность обусловила широкое распространение систем сигналов с равной энергией, которые обычно называют системами с активной паузой. Это особенно важно для каналов с замираниями, в которых коэффициент передачи флуктуирует (см. §6.7).

Заметим, что для двоичной системы неравенство (6.27) можно представить в более простом виде:

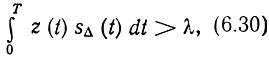
где s_Δ (0 = s₁ (t) - s₀(t) - разностный сигнал; λ = 0,5(E₁-Е₀) - пороговый уровень. Для системы с активной паузой Х=0, что значительно облегчает реализацию оптимальной схемы.

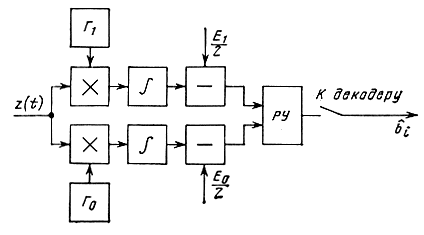
Рис. 6.4. Оптимальный демодулятор при точно известных сигналах, построенный по корреляционной схеме

При выполнении неравенства (6.30) регистрируется символ 1, в противном случае - 0. Для реализации (6.30) в схеме рис. 6.4 требуется лишь одна ветвь.

На рис. 6.5,а показана схема, реализующая алгоритм (6.30) для двоичной системы передачи однополярными импульсами (с пассивной паузой): s₁(t) = a, s₀(t) = 0. При этих сигналах s_Δ (t) = s₁(t) = a, Е₁ = а²Т, E₀ = 0, λ = а²T/2 и (6.30) примет следующий, вид:

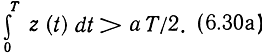
Рассмотренную систему двоичных сигналов используют в простейших устройствах проводной связи. В радиоканалах, а также в современных кабельных каналах применяют высокочастотные сигналы. Наиболее простыми двоичными системами с гармоническими сигналами являются системы с амплитудной (AM), фазовой (ФМ) и частотной (ЧМ) манипуляцией.

В двоичной AM s₁(t) = acos(ω₀t + φ), s₀(t) = 0. Все входящие сюда постоянные (а, ω₀, φ) в этом параграфе полагаем известными. Поскольку здесь s_Δ(t) = s₁(t), Е₁ = а²Т/2 и E₀ = 0, правило (6.30) запишется так:

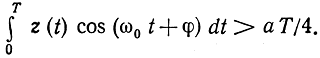
Оно реализуется схемой рис. 6.5,6, которая отличается от рис. 6.5,a блоком перемножения приходящего сигнала с опорным сигналом cos(ω₀t + φ). Пороговый уровень λ̇ в этом случае равен aT/(4RC).

При двоичной ФМ системе s₀(t) = a cos(tω₀ + φ), s₀(t) = а cos (tω₀ + φ + π) = -s₁(t). Это - система с активной паузой, и поэтому в (6.30) λ = 0. Легко убедиться, что правило решения сводится при этом к следующему:

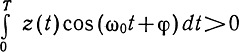
и реализуется той же схемой рис. 6.5,6 при λ̇ = 0. В этом случае РУ играет роль дискриминатора полярностей.

Рис. 6.5. Реализация оптимального приема двоичных прямоугольных импульсов (а) и реализация оптимального приема в двоичной системе AM, ФМ при точно известном сигнале (б)

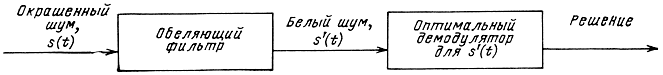
Рис. 6.6. Оптимальный демодулятор с обеляющим фильтром при гауссовском 'окрашенном' шуме

Рассмотрим вкратце случай, когда гауссовский шум в канале не белый и не квазибелый, а "окрашенный", т. е. имеет неравномерную плотность мощности G(f) в полосе спектра сигнала. Пропустим приходящую на вход демодулятора сумму сигнала и шума через фильтр с передаточной функцией k(i2πf), такой чтобы в полосе спектра сигнала произведение G(f) |k(i2πf)|² было постоянной величиной N₀. Из всех возможных фильтров с k(i2πf), удовлетворяющих этому условию и различающихся только фазо-частотной характеристикой, можно выбрать минимально фазовый, который является обратимым. Очевидно, что на выходе фильтра шум окажется квазибелым: G_вых(f)=N₀. Поэтому такой фильтр называется обеляющим.

Сигнал s_i(t) после прохождения через обеляющий фильтр превратится в некоторый другой сигнал, который обозначим s'_i(t). Вид его можно определить, зная s_i(t) и k(i2πf). Если теперь подать колебания с выхода обеляющего фильтра на демодулятор, являющийся оптимальным для приема сигналов s'_i(t) (i = 0, 1, ..., m-1), то получим схему рис. 6.6, которая, очевидно, является оптимальной для сигналов s_i(t) при окрашенном шуме.

Следует обратить внимание на то, что в схеме рис. 6.2, 6.4 и 6.5 опорный сигнал должен иметь те же начальные фазы, что и ожидаемые приходящие сигналы или, другими словами, должен быть когерентным с приходящими сигналами. Это требование обычно затрудняет реализацию демодулятора и требует введения в него, помимо указанных на рисунках блоков, дополнительных устройств, предназначенных для регулировки фаз опорных сигналов.

Все методы приема, для реализации которых необходимо точное априорное знание начальных фаз приходящих сигналов, называют когерентными. В тех случаях, когда сведения о начальных фазах ожидаемых сигналов извлекаются из самого принимаемого сигнала (например, если фаза флуктуирует, но настолько медленно, что может быть предсказана по предыдущим элементам сигнала), прием называют квазикогерентным. Если же сведения о начальных фазах приходящих сигналов отсутствуют или по каким- либо соображениям их не используют, то прием называют не когерентным (см. § 6.6).