6.4. Реализация алгоритма оптимального приема на основе согласованных фильтров

Скалярное произведение (6.28) можно вычислить не только с помощью активного фильтра (коррелятора), описанного в предыдущем параграфе, но и с помощью пассивного линейного фильтра

с постоянными параметрами. Если на вход фильтра подать принимаемый сигнал z(t), то напряжение на выходе фильтра

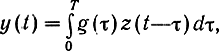
-импульсная реакция фильтра. Выберем ее такой, чтобы в момент t = T получить значение y(Т), совпадающее со скалярным произведением (6.28). Легко видеть, что это будет выполнено, если g(x) = s_i(T-τ). Действительно, при этом

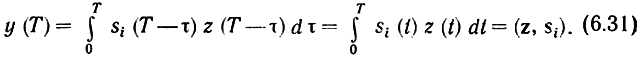
Такой фильтр называется согласованным с сигналом s_i(t). В более общем смысле фильтром, согласованным с сигналом s(t), называют линейный фильтр с, постоянными параметрами и импульсной реакцией:

где a, t₀ - постоянные. Функция g(t) является зеркальным отображением s(t) относительно оси, проведенной через точку t₀/2 (рис. 6.7). Для физической реализуемости фильтра необходимо и достаточно, чтобы g(t) = 0 при t<0. В частности, для финитного сигнала s(t), поступающего на вход фильтра в момент t = 0 и заканчивающегося в момент T, условие физической реализуемости согласованного фильтра заведомо выполняется, если постоянная t₀ (момент отсчета) удовлетворяет условию

Действительно, при этом (t₀-t)>T и s(t₀-t)=0, если t<0. Реакция согласованного фильтра на финитный сигнал s(t) длительностью Т существует лишь на финитном интервале протяженностью 2Т.

Передаточная функция согласованного фильтра с импульсной реакцией (6.32) определяется преобразованием Фурье

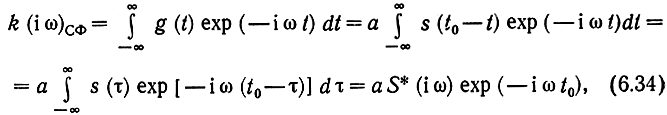
где S*(iω)-функция, комплексно-сопряженная со спектральной плотностью сигнала s(i). Следовательно, с точностью до коэффициента а амплитудно-частотная характеристика согласованного фильтра определяется амплитудным спектром сигнала s(t) (т. е. фильтр хорошо пропускает те частоты, которые дают больший вклад в энергию сигнала), а его фазо-частотная характеристика (без учета слагаемого - ω₀t, определяемого задержкой t₀) обратна по знаку фазовой характеристике сигнала s(t). Благодаря этому в момент t₀ все составляющие спектра принимаемого сигнала складываются в фазе и дают максимальный отклик.

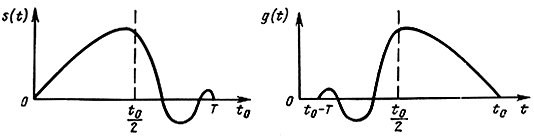
Рис. 6.7. Сигнал s(t) и импульсная реакция g(t) линейного фильтра, согласованного с этим сигналом

Согласно (6.31) в момент времени Т напряжение на выходе согласованного фильтра пропорционально сигналу на выходе интегратора активного фильтра в схеме рис. 6.4. Поэтому демодулятор, реализующий алгоритм (6.25), может быть выполнен и на базе согласованных фильтров. Структурная схема такого демодулятора для двоичной системы показана на рис. 6.8, где СΦ_i - фильтр, согласованный с сигналом s_i(t).

Если на вход фильтра подан тот сигнал, с которым он согласован, то сигнальная составляющая на выходе согласованного фильтра

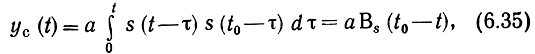
где B_s(t₀-t) -временная функция корреляции сигнала. Следовательно, формы полезного сигнала на входе и выходе согласованного фильтра, как правило, существенно отличаются друг от друга. Следует еще раз подчеркнуть, что задачей согласованного фильтра является не восстановление формы сигнала, искаженной шумом, а получение одного отсчета, по которому можно судить о присутствии или отсутствии на входе фильтра сигнала известной формы.

Отметим одно важное свойство согласованного фильтра, которое иногда рассматривается как его определение. Будем подавать сумму детерминированного сигнала и белого шума Z(t) = s(t) + N(t) на вход различных линейных цепей с постоянными параметрами и измерять в момент t = t₀ отношение мгновенной мощности сигнальной составляющей к средней мощности шума на выходе цепи. Докажем, что это отношение р_пик максимально, если цепь является согласованным фильтром.

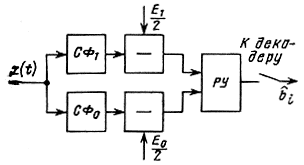
Рис. 6.8. Оптимальный демодулятор на основе согласованных фильтров

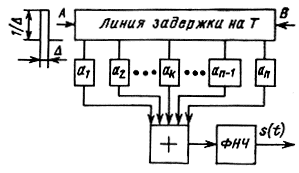
Рис. 6.9. Реализация фильтра, согласованного с произвольным непрерывным сигналом на основе линии задержки с отводами и блоками взвешивания

Пусть S(iω)-спектр входного сигнала, a k(iω)-передаточная функция некоторой линейной цепи. Тогда спектр сигнальной составляющей y_c(t) на выходе цепи равен S(iω)k(iω). С помощью обратного преобразования Фурье найдем значение в момент t=t0:

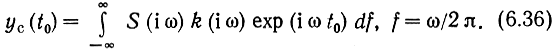
Мощность шума на выходе цепи

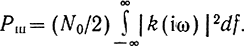
Искомое отношение

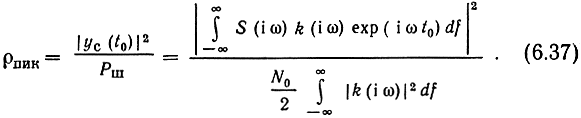
Согласно неравенству Буняковского- Шварца (2.93), (2.103) для любых комплексных функций А(х) и В(х) при

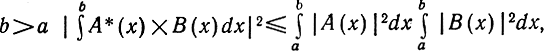
причем равенство имеет место только при

где α - произвольная постоянная.

Применим неравенство Буняковского - Шварца к числителю (6.37). Если положить

то получим

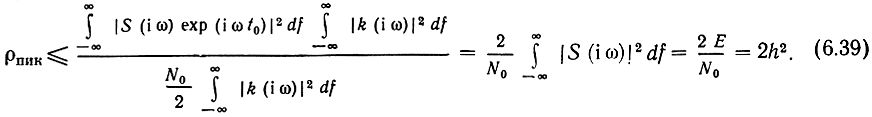
где h² =E/N₀ - отношение энергии элемента сигнала Е на входе фильтра к спектральной плотности N₀ белого шума.

Знак равенства согласно (6.38) и (6.39) имеет место тогда, когда передаточная функция удовлетворяет (6.34), т. е. для согласованного фильтра, что и требовалось доказать.

Рассмотрим возможности реализации согласованных фильтров. Согласованный фильтр для финитного сигнала произвольного вида s(t) можно, в принципе, построить на основе неискажающей длинной линии, обеспечивающей задержку сигнала на время T, с бесконечной плотностью отводов. Практически можно брать отводы в дискретных точках с разносом Δt = 0,5/F, где F - эффективная ширина спектра сигнала.

Действительно, с помощью схемы, показанной на рис. 6.9, можно с хорошей точностью синтезировать любой сигнал s(t), представленный усеченным рядом Котельникова (2.106):

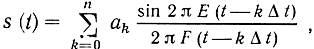
где a_k = s(kΔt); Δt = 1/(2F); F - ширина спектра сигнала. Как было показано в § 2.7, такой сигнал можно получить на выходе идеального ФНЧ с полосой пропускания F, подавая на его вход последовательность δ-импульсов с весами а_k через интервалы времени Δt. Это осуществляется с известным приближением в схеме рис. 6.9. Если на вход А линии в начальный момент подается один короткий единичный импульс, аппроксимирующий δ-функцию, то с отводов снимаются такие же импульсы, разнесенные на интервалы Δt, которые, пройдя через взвешивающие блоки а_k, поступают поочередно на вход ФНЧ. Взвешивающие блоки содержат аттенюаторы или усилители с коэффициентом усиления |а_k|, а также при отрицательных а_k - инверторы.

Таким образом, схема рис. 6.9 представляет собой линейный фильтр, называемый трансверсальным, с импульсной реакцией s(t). Легко видеть, что если входной импульс подать не в точку A, а в точку В, то будет синтезирован сигнал, представляющий зеркальное отображение s(t). Поэтому та же схема со входом в точке В оказывается фильтром, согласованным с s(t).

Существуют различные другие способы реализации фильтра, точно или приближенно согласованного с сигналом заданной формы. Так, например, фильтр, согласованный с прямоугольным импульсом длительностью T, "который по определению (6.32) должен иметь импульсную реакцию также в форме прямоугольного импульса, можно построить по схеме рис. 6.10,а, содержащей конденсатор, линию задержки на время T, инвертор и сумматор. Если на вход этого фильтра подать единичный импульс (дельта-функцию), то он зарядит конденсатор до некоторого напряжения. Затем спустя время Т через линию задержки и инвертор такой же входной импульс противоположной полярности поступит на конденсатор и разрядит его. Как следствие, на выходе фильтра образуется в качестве импульсной реакции прямоугольный импульс.

Рис. 6.10. Реализация согласованных фильтров: а - для прямоугольного импульса; б -для прямоугольного радиоимпульса

Вариант фильтра, согласованного с прямоугольным радиоимпульсом s(t) = а cos(tω₀ + φ₀), заданным на интервале (0, T), показан на рис. 6.10,6. Он состоит из идеального колебательного контура без потерь^*, настроенного на частоту ω₀ и фазовращателя, сдвигающего фазу колебаний контура на -ω₀Т-φ₀. Линия задержки на T в схеме и инвертор обеспечивают гашение колебаний фильтра вне интервала (0, T), импульсная же реакция фильтра на этом интервале с учетом фазовращателя acos [ω₀(t-Т)-φ₀] = а cos[ω₀(T-i)+φ₀] = as(T-t), что и обеспечивает согласование согласно (4.31).

^* (В реальном фильтре всегда имеются потери, но если затухание контура достаточно мало (βT<<1), то импульсная реакция контура а е^-βt cos ω₀t при практически не отличается от a cos ω₀t. Для уменьшения β применяют электромеханические фильтры (кварцевые и другие), а также используют схемы с положительной обратной связью.)

Схема с согласованными фильтрами на первый взгляд кажется проще схемы с активными фильтрами, поскольку в ней нет опорных генераторов и не возникает проблемы обеспечения их когерентности (согласования по фазе с приходящим сигналом). Однако и в схеме с согласованными фильтрами имеются свои практические трудности. В этом можно убедиться, сравнив, например, эпюры напряжений (без учета помех в канале) на выходе фильтра (рис. 6.11,6), согласованного с прямоугольным радиоимпульсом (рис. 6.11,а), и на выходе интегратора активного фильтра (рис. 6.11,в). Отметим, что всюду, за исключением точки t = T, напряжения на выходах обоих фильтров отличаются друг от друга. Из рисунков видно, что допустимая неточность во времени Δt снятия отсчета максимума сигнала на выходе активного фильтра значительно больше, чем при снятии отсчета максимума сигнала на выходе согласованного фильтра. При активном фильтре достаточно потребовать, чтобы неточность взятия отсчета была мала по сравнению с тактовым интервалом Т, а при согласованном фильтре - по сравнению с периодом высокочастотного заполнения радиоимпульса (так называемый когерентный отсчет). Трудность обеспечения когерентного отсчета в согласованном фильтре вполне соизмерима с трудностью реализации когерентных опорных генераторов в активном фильтре.

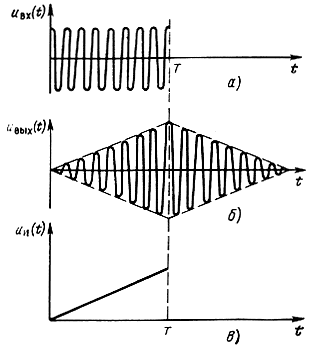
Рис. 6.11. Сигналы на выходе согласованного фильтра и корреляционной схемы при подаче па вход прямоугольного радиоимпульса: а - импульс на входе; б - импульс на выходе согласованного фильтра; в - напряжение на выходе интегтора активного фильтра

Если на вход фильтра, согласованного с сигналом s(t), подать сигнал z(t), то огибающая на выходе фильтра в момент отсчета Т равна нулю тогда и только тогда, когда сигналы s(t) и z(t) ортогональны на интервале (0, Т) в усиленном смысле (см. с. 63). Легко убедиться, что если s(t) и z(t) ортогональны, но не в усиленном смысле, то в момент отсчета мгновенное напряжение сигнала на выходе фильтра равно нулю, однако огибающая отлична от нуля.

В технике связи для фильтрации сигнала на фоне шума часто вместо согласованных используют фильтры, характеристики которых лишь частично согласованы с характеристиками сигнала. Такие фильтры называют квазиоптимальными.

Так, в практике радиоприема используются так называемые квазиоптимальные линейные фильтры, форма частотных характеристик которых заранее задана и максимум параметра ρ_пик обеспечивается лишь соответствующим подбором ширины полосы пропускания фильтра. Квазиоптимальный фильтр такого типа впервые исследовался В. И. Сифоровым, который рассматривал прохождение одиночного радиоимпульса с прямоугольной огибающей через идеальный полосовой фильтр с полосой пропускания Δf на фоне квазибелого шума.

Воспользовавшись формулой (6.37), В. И. Сифоров показал, что при Δf = 1,37/Т отношение ρ_пик достигает максимума;

Сравнив (6.39) и (6.40), можно видеть, что при приеме одиночного импульса энергетический выигрыш оптимального фильтра по сравнению с квазиоптимальным невелик (не превышает 1 дБ).

Таким образом, при приеме одиночных радиоимпульсов вполне допустимо ограничиться квазиоптимальной фильтрацией. Положение, однако, существенно меняется, если надлежит принимать информационные импульсы, следующие друг за другом с таким интервалом, на котором переходные процессы в квазиоптимальном фильтре не успевают затухать. В этих условиях качество приема с квазиоптимальной фильтрацией резко падает, в то время как при использовании оптимального согласованного фильтра качество остается прежним, так как сигнал на его выходе концентрируется на ограниченном временном интервале и к моменту отсчета для одного импульса реакция на все предыдущие импульсы равна нулю (см., например, рис. 6.11,6).