6.5. Потенциальная помехоустойчивость при точно известном ансамбле сигналов

Определим потенциальную помехоустойчивость для двоичной системы с аддитивным белым шумом, когда при приеме точно известны оба ожидаемых сигнала: s₁(t) и s₀(t), полагая, что априорные вероятности этих сигналов одинаковы. Приходящий сигнал Z(t) является случайным, так как, во-первых, заранее неизвестны реализация передаваемого сигнала, во-вторых, он содержит случайную помеху N(t).

В этом случае согласно (6.30) алгоритм оптимального приема

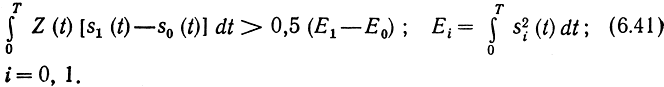
При выполнении неравенства (6.41) оптимальный приемник регистрирует символ 1, соответствующий сигналу s₁(t), в противном случае-символ 0, соответствующий сигналу s₀(t). Если действительно передается символ 1, то Z(t) = s₁(t) + N(t). При этом вероятность ошибки р(0|1) определится вероятностью того, что неравенство (6.41) не выполнено, т. е. вероятностью выполнения неравенства

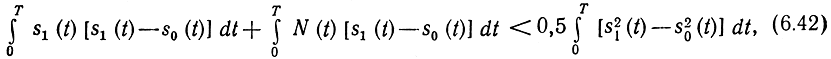
которое легко привести к следующему виду:

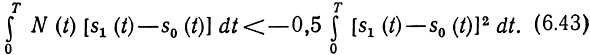
Аналогичное соотношение получится, если предположить, что передается символ 0. Следовательно, в обоих случаях вероятности ошибки равны: р(0|1) = (1|0) = р и сформированный модемом двоичный дискретный канал симметричен.

Запишем (6.43) в виде

где

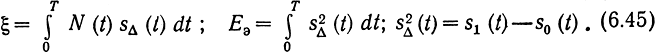
Если N(t) -нормальный стационарный белый шум с нулевым средним и односторонней спектральной плотностью мощности N₀, то ξ - нормально распределенная величина, так как она определяется линейной операцией над нормальным же случайным процессом. Ее математическое ожидание

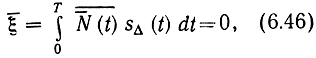
а дисперсия

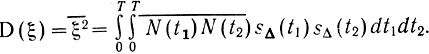
Учитывая выражение (2.49) для ФК белого шума

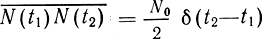
и фильтрующее свойство δ-функции, получим

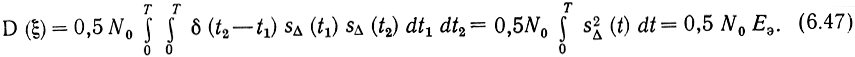
Поэтому вероятность выполнения неравенства (6.44), т. е. вероятность ошибки

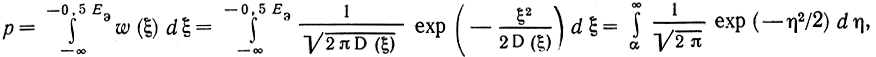
где произведена замена переменной

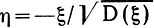
и введено обозначение

Функция

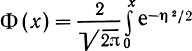
табулирована и называется функцией Крампа^*. Учитывая, что Φ(∞) = 1, можно (6.48) записать в виде

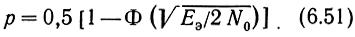
^* (В литературе часто через F(x) обозначают функцию

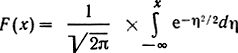
(гауссовский интеграл ошибок). Очевидно, что гауссовский интеграл ошибок

F(x)=0,5[1+Φ(x)]. (6.50)

Иногда в справочниках табулируется функция

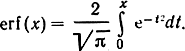
Нетрудно видеть, что

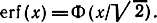
В литературе встречается также дополнение к)

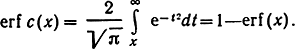
При заданной интенсивности помехи N₀ потенциальная помехоустойчивость двоичной системы, на что впервые обратил внимание В. А. Котельников, зависит только от так называемой эквивалентной энергии сигналов

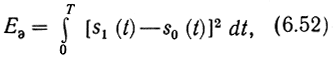
которая равна квадрату расстояния между сигнальными точками в пространстве Гильберта. Помехоустойчивость выше (вероятность ошибки меньше) у той системы, у которой больше эквивалентная энергия используемых сигналов, независимо от формы используемых сигналов. Последние, в частности, могут быть как простыми (отрезками синусоиды с малой базой), так и сложными (шумоподобными, с большой базой).

На рис. 6.12 в двумерном пространстве показаны точки сигналов для двоичной системы: рис. 6.12,а - AM при s₀(t) = 0,

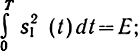
рис. 6.12,6 - ЧМ с ортогональными сигналами

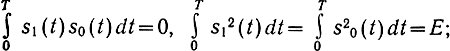
рис. 6.12,6 - ФМ с противоположными сигналами s₁(t) =-s₀(t).

Из рисунка видно, что по сравнению с двоичной AM для двоичной ЧМ эквивалентная энергия сигналов E_э = ||s₁-s₂||² в 2 раза больше, а для двоичной ФМ в 4 раза больше.

Соотношение (6.52) позволяет осуществлять оптимальный выбор сигналов s₁(t) и s₀(t) или соответственно u₁(t) и u₀(t), обеспечивающих максимально возможную помехоустойчивость при заданной энергии сигналов Е. В самом деле, для такой оптимальной системы величина Е_э должна быть максимальной при условии, что

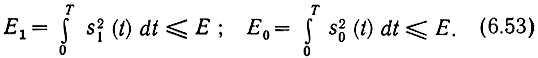
Можно написать

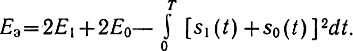
Для получения максимума этого выражения нужно сделать Е₁ и Е₀ возможна большими, а интеграл в правой части - как можно меньшим. Максимально возможные значения Е₁ и Е₀ получатся, если, учитывая условия (6.53), положить

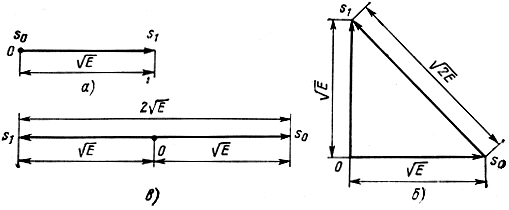
Рис. 6.12. К определению эквивалентной энергии двоичных систем AM, ЧМ,

Интеграл

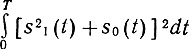
принимает только неотрицательные значения, поэтому его минимум равен нулю и достигается при условии

которое не противоречит условию (6.54). Таким образом, в двоичном канале с постоянными параметрами и аддитивной флуктуационной помехой оптимальной оказывается система с противоположными сигналами (6.55). Этому условию удовлетворяют, например, двухполярные импульсы, сигналы двоичной фазовой модуляции (ФМ), если разность фаз сигналов Δφ = π и т. п. Для всех таких систем Е_э = 4Е и вероятность ошибки

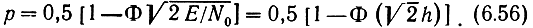
где h² = E/N₀ - отношение энергии сигнала на входе демодулятора

к спектральной плотности флуктуационной помехи.

Для системы с активной паузой и ортогональными сигналами (например, при известных условиях для системы двоичной ЧМ), когда

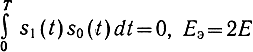
и минимальная вероятность ошибки

Сравнивая (6.56) и (6.57), приходим к выводу, что переход от системы с ортогональными сигналами к системе с оптимальными (противоположными) сигналами позволяет в рассматриваемом канале обеспечить неизменное качество связи (вероятность ошибки) при понижении средней мощности передатчика в 2 раза, т. е. дает энергетический выигрыш в 2 раза (или на 3 дБ). Этот вывод следует также из рис. 6.12.

В двоичной системе с пассивной паузой, полагая s₀(t) = 0 и

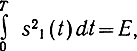
получаем для минимальной вероятности ошибки о

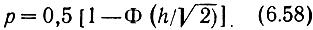
Отсюда видно, что при переходе от системы AM к системе ЧМ энергетический выигрыш по максимальной мощности равен 2, а при переходе к системе ФМ - 4. Если же сравнение вести не по пиковой, а по средней мощности, то переход от AM к ЧМ не дает энергетического выигрыша, поскольку при ЧМ средняя мощность равна максимальной, а при AM - вдвое меньше максимальной (если s₁ и s₀ передаются с одинаковой вероятностью).

Тем не менее, когда в начале 40-х годов в радиосвязи стали применять ЧМ, помехоустойчивость значительно возросла по сравнению с ранее используемой системой AM. Это объясняется не увеличением потенциальной помехоустойчивости, которая для обеих систем одинакова, а, главным образом, тем, что оптимальная решающая схема для ЧМ реализуется с довольно большой точностью, а при AM этому препятствует невозможность обеспечить точное оптимальное значение ненулевого порогового уровня X (см. рис. 6.5). Поэтому реальная помехоустойчивость при ЧМ близка к потенциальной, а при AM значительно ниже ее.

Система ФМ, как и другие системы с противоположными сигналами, обеспечивает максимальную для двоичной системы потенциальную помехоустойчивость. Однако реализация демодулятора для когерентного приема ФМ встречает определенные трудности. При построении демодулятора с активным фильтром (см. рис. 6.5) возникает проблема поддержания равенства фаз опорного генератора и приходящего сигнала. Если пытаться строить его на основе согласованного фильтра (см. рис. 6.11), то возникает еще более трудная задача когерентного отсчета.

В практических схемах опорный сигнал s₁(t) формируется из принимаемого колебания, поскольку если его генерировать автономным генератором в месте приема, то необходимое согласование по фазе не может быть обеспечено вследствие неизбежных флуктуаций. Поэтому необходимо по принимаемому сигналу восстановить немодулированный гармонический сигнал cos(ω₀t+φ₀).

Задача выделения опорного сигнала особенно затрудняется при ФМ, так как если элементы s₁(t) и s₀(t) = -s₁(t) передаются равновероятно, то спектр сигнала ФМ вообще не содержит составляющей на частоте ω₀. Для ее получения приходится использовать нелинейные устройства снятия модуляции. Это достигается различными схемами, например, схемой, предложенной в 1933 г. А. А. Пистолькорсом. Схема содержит умножитель частоты на 2, выходной сигнал которого через узкополосный фильтр, настроенный на частоту 2ω₀, поступает на делитель частоты на 2. Если сигнал на входе множителя записать в виде u₁ = cos (ω₀t+kπ+φ₀)> k = 0 или k = 1, то сигнал на выходе умножителя u₂ = cos(2ω₀t + 2φ₀), а сигнал на выходе делителя u₃ = cos(ω₀t + φ₀).

Однако все схемы формирования опорного сигнала таковы, что вследствие различных неконтролируемых факторов возможны случайные изменения знака опорного сигнала. Это, в частности, относится и к делителю частоты на 2 в схеме А. А. Пистолькорса, поскольку эта операция неоднозначна - фаза выходного сигнала делителя может принять любое из двух значений: 2φ₀/2 или 2φ₀/2 + π = φ₀ + π. Это означает, что символы, регистрируемые на выходе приемника даже при отсутствии аддитивной помехи в канале [z(t) = s₁(t)], после случайного перескока фазы опорного сигнала инвертируются (нули будут записаны как 1, а 1 как 0). Это будет продолжаться до следующего перескока фазы опорного сигнала. Возникает так называемое явление "обратной работы", вследствие которого практическое внедрение систем с двоичной фазовой модуляцией оказалось невозможным.

Эффективный метод устранения этого явления был найден путем перехода к относительным методам модуляции, предложенным Н. Т. Петровичем (см. § 1.5). Они сводятся к модуляции информационного параметра передаваемой посылки элемента сигнала относительно того же параметра предшествующей посылки. При относительной фазовой манипуляции (ОФМ) сообщение содержится не в абсолютном значении фазы элемента сигнала, а в разности фаз двух соседних элементов, при этом символ 1 передается повторением той реализации сигнала, которая имела место в качестве предыдущего элемента, а символ 0 - передачей реализации с обратной фазой, либо наоборот.

Сигналы ОФМ могут приниматься различными методами. Здесь рассмотрим квазикогерентный прием сигналов ОФМ (называемый методом сравнения полярностей). Заметим сначала, что систему ОФМ можно рассматривать как обычную систему с фазовой модуляцией (ФМ), но со специальным перекодированием символов. Это означает, что оптимальный прием сигналов ОФМ можно осуществить, например, схемой рис. 6.5, но с перекодированием принятых символов. Перекодирование выполняется сравнением полярностей напряжений на выходе интегратора для двух соседних элементов, для чего, естественно, требуется задержка выходных символов в ячейке памяти (ЯП) на время Т. Такая схема демодулятора показана на рис. 6.13 (без устройства подстройки фазы опорного генератора Γ, которое может быть выполнено, например, по схеме Пистолькорса). Так как ОФМ-система с активной паузой, то пороговый уровень в демодуляторе - нулевой и решающее устройство превращается в дискриминатор полярности (ДП). Полярности соседних элементов сравниваются в схеме сравнения полярностей (ССП), которая представляет собой обычный перемножитель. Символ 1 регистрируется на выходе приемника, например, при совпадении полярностей двух соседних посылок, символ 0 - если эти полярности различны. При таком методе приема перескок фазы опорного сигнала (при отсутствии помехи в канале) вызывает ошибку только в одном символе. Последующие же символы регистрируются правильно, т. е. явление "обратной работы" не возникает.

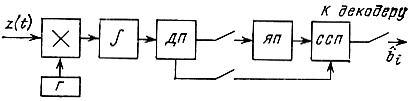
Рис. 6,13. Схема оптимального приема сигналов ОФМ методом сравнивания полярностей (когерентный прием)

Определим вероятность ошибки в системе ОФМ при учете флуктуационной помехи в канале при когерентном приеме. Вероятность p_ОФМ ошибочной регистрации символов в системе ОФМ при приеме по методу сравнения полярностей не совпадает с вероятностью

появления ошибок на выходе фазового детектора или, что то же самое, с вероятностью ошибок в системе "классической" фазовой манипуляции, определяемой (6.56). Очевидно, что ошибочная регистрация символа при приеме методом сравнения полярностей возможна в результате одного из двух несовместимых событий: а) знак данного элемента принят ошибочно, а знак предыдущего - верно; б) знак данного элемента принят верно, а предыдущего - ошибочно. Каждое из этих событий имеет вероятность р ф J1-РФЖ) - Таким образом,

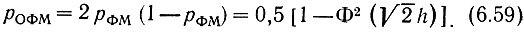
В нормальных условиях эксплуатации, когда требуется p_ФМ <<1,

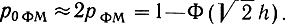
Таким образом, "платой" за устранение обратной работы является удвоение вероятности*, ошибки, обусловленной шумом в канале.

Очевидно, что при рассматриваемом методе приема сигналов ОФМ образующийся дискретный канал является марковским (см. с. 95). Вероятность ошибки в нем зависит от того, правильно или ошибочно принят предыдущий символ. Подавляющее большинство ошибок группируется по две.

Для не двоичных систем (m>2) нахождение вероятности ошибочного приема рт в общем случае затрудняется, так как теперь приходится анализировать совокупность из (m-1) неравенств. Однако для систем с активной паузой (Е_i = Е) при равновероятных ортогональных сигналах канал симметричен и можно оценить вероятность рт простым неравенством

где р₂ - вероятность ошибки для двоичной системы в том же канале, если используется некоторая пара из m сигналов.