6.7. Прием дискретных сообщении в каналах с замираниями. Разнесенный прием

В большей части радиоканалов, а также в некоторых других каналах флуктуирует не только начальная фаза, но и амплитуда ожидаемых сигналов s_i(t) (коэффициент k). При относительно быстрых (по сравнению с длительностью посылки Т) замираниях сигнала нельзя сколь-нибудь определенно судить по результатам приема предыдущих элементов о значениях амплитуд и фаз последующих элементов. Найдем оптимальный алгоритм приема при этих условиях.

Пусть канал описывается моделью (3.32), т. е. является однолучевым гауссовским с общими замираниями. Алгоритм оптимального приема в условиях флуктуации как фазы, так и амплитуд сигнала можно (на основе правила максимального правдоподобия) получить, вычисляя математическое ожидание (6.66) по k:

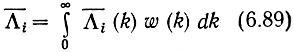
и сравнив между собой отношения правдоподобия Λ̄_i с различными индексами i. Однако для систем с активной паузой результат легко указать и без дополнительных выкладок - он определяется

соотношением (6.72). Это очевидно, так как (6.72), являясь алгоритмом приема при неопределенной фазе, не зависит от амплитуды (коэффициента k), следовательно, этот алгоритм остается оптимальным при любом законе распределения амплитуд. При этом, однако, помехоустойчивость приема существенно зависит от распределения k.

Определим, например, вероятность ошибки для двоичной системы с активной паузой, ортогональной в усиленном смысле при условии, что замирания в канале медленные, т. е. когда k можно считать неизменным на протяжении элемента сигнала Т₀ и мало меняющимся от посылки к посылке.

Если условную вероятность ошибки при некотором фиксированном значении k обозначить р_k, то безусловная вероятность ошибки при медленных замираниях

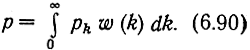
В данном случае условная вероятность ошибки определяется формулой (6.82), в которой величина

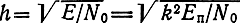
пропорциональна k. Здесь Е_Π - энергия сигнала на входе канала (на передатчике). Очевидно, что между значениями h, k и математическими ожиданиями их квадратов существует зависимость

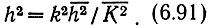
Пусть, например, k имеет распределение Рэлея (3.35), которое можно представить в следующей форме:

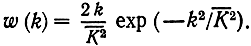
Подставив это в (6.90) и обозначив

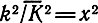
с учетом (6.82) и (6.91), найдем вероятность ошибки для двоичных ортогональных в усиленном смысле сигналов при рэлеевских замираниях:

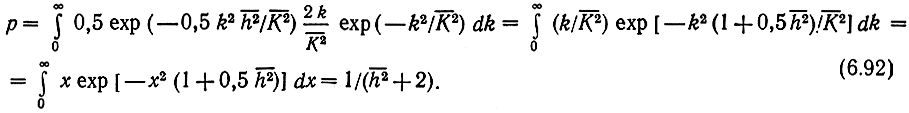
Эта зависимость представлена на рис. 6.16 кривой 4.

Аналогично определяется вероятность ошибок и при других законах замираний. Так, например, если распределение вероятностей К - обобщенное рэлеевское (3.36), то

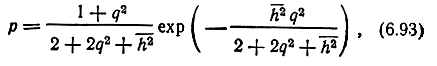
где q² - отношение мощностей регулярной и флуктуирующей составляющих. На рис. 6.16 (кривая 3) показана эта зависимость при q² = 1; 5 и 10. Легко проверить, что при q² = ∞ (отсутствие замираний) формула (6.93) переходит в (6.82), а при q² = 0 (отсутствие регулярной составляющей) - в формулу (6.92).

Приведем еще результат для случая, когда случайная величина К распределена по одностороннему нормальному закону:

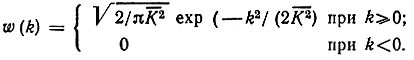
Это имеет место в очень плохих радиоканалах. При этом

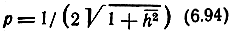
(см. рис. 6.16, кривая 5).

Для общего гауссовского канала выражения вероятности ошибок можно найти в [6].

Заметим, что все полученные для двоичных систем выражения вероятностей ошибок при h² (или h̄²), стремящемся к нулю, принимают значение 0,5. Это и следовало ожидать, так как при р = 0,5 по двоичному каналу никакая информация не передается (см. рис. 3.9 и относящиеся к нему пояснения). При h²→∞ вероятность ошибок стремится к нулю. Это значит, что во всех рассмотренных каналах можно получить сколь угодно малую вероятность ошибки, увеличивая мощность сигнала. Однако степень этого увеличения различна для разных каналов. Сравнение кривых на рис. 6.16 показывает, что при замираниях сигнала помехоустойчивость систем связи значительно ниже, чем в канале без замираний при той же средней мощности передатчика. Для поддержания заданного качества связи в этих условиях приходится иметь определенный запас мощности передатчика.

Вероятность ошибок при приеме дискретных сообщений можно существенно уменьшить с помощью разнесенного приема, сущность которого заключается в том, что демодулятор принимает решение о переданном символе не по одному, а по двум или более сигналам, несущим одну и ту же информацию. Разнесенный прием является одним из основных способов повышения помехоустойчивости связи при замираниях сигнала.

В радиосвязи применяются различные способы разнесенного приема: по времени или метод накопления (он сводится к повторению сигнала несколько раз); по частоте (сигнал дублируется по многим частотным каналам); прием сигнала на различные антенны, разнесенные в пространстве; поляризационное разнесение (прием на антенны, расположенные в одном месте, но принимающие электромагнитные волны разной поляризации); разнесение по отдельным лучам в многолучевом канале. В последнем случае лучи разделяются либо остро направленными антеннами по углу прихода в горизонтальной или вертикальной плоскости (такой способ применяется, главным образом, на УКВ), либо по времени прихода (времени запаздывания). Можно показать, что разделение лучей по времени прихода требует применения шумоподобных сигналов.

Из перечисленных методов в радиосвязи наиболее распространен прием на разнесенные в пространстве антенны. На втором месте - разнесенный прием по частоте, используемый в различных каналах. Остальные методы разнесения также применяются, но значительно реже.

В каналах без замираний разнесенный прием повышает верность, если имеется возможность сложить пришедшие по n ветвям сигналы когерентно, т. е. сводя имеющиеся между ними разности начальных фраз к пренебрежимо малому значению.

При когерентном сложении одинаковых сигналов суммарный сигнал будет иметь в п раз большую "амплитуду", т. е. в n² раз большую мощность, чем отдельный сигнал. При этом помехи, которые обычно в различных ветвях независимы, складываются не когерентно, так что мощность суммарной помехи будет только в n раз больше мощности помехи в одной ветви. В результате отношение мощности сигнала к мощности помехи увеличится в n раз.

Можно показать, что если по n ветвям принимаются сигналы с различными мощностями, а помехи, присутствующие в них, имеют различную интенсивность, то наилучшие результаты получаются при когерентном сложении сигналов, умноженных на весовые коэффициенты, пропорциональные

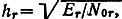
где Е_r - энергия элемента приходящего сигнала, a N_0r - спектральная плотность шума в r-й ветви (r = 1, ..., n). При этом в суммарном сигнале отношение h²_э энергии сигнала к спектральной плотности шума

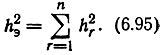
В каналах с замираниями имеется и другой, более эффективный механизм повышения верности при разнесенном приеме. Его можно грубо пояснить так: при одиночном приеме ошибки возникают, главным образом, тогда, когда уровень сигнала упадет ниже некоторого порогового значения, а при разнесенном приеме- когда уровень сигнала окажется ниже порогового во всех ветвях. Если замирания в ветвях слабо коррелированны, то вероятность одновременного падения уровней сигнала во всех ветвях очень мала.

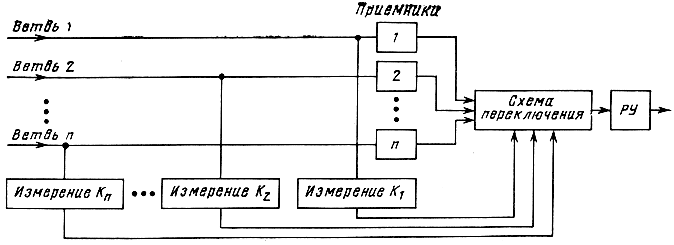
Рис. 6.21. Схема разнесенного приема при автовыборе ветвь с наиболее сильным сигналом

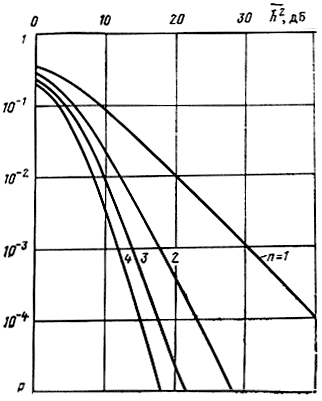
Рис. 6.22. Зависимость вероятности ошибки при разнесенном приеме в канале с рэлеевскими замираниями от h̄² (двоичная система с активной паузой, ортогональная в усиленном смысле при автовыборе ветви с наиболее сильным сигналом), n - число ветвей разнесения

Существуют различные способы комбинированных ("сложения") сигналов отдельных ветвей разнесения при приеме. Не останавливаясь на исследовании оптимальных способов сложения (разнесенного приема) в каналах с замираниями, отметим наиболее простой, достаточно эффективный и широко распространенный способ автовыбора ветви с наиболее сильным сигналом (см. рис. 6.21). В этой схеме постоянно измеряется коэффициент передачи канала Кг (или мощности принимаемого сигнала) по отдельным ветвям (приемникам), а к демодулятору подключается приемник с наиболее сильным сигналом.

На рис. 6.22 показана зависимость вероятности ошибок при не когерентном разнесенном приеме. Здесь n - число ветвей разнесения.