7.8. Теория нелинейной фильтрации

Во многих случаях сигнал s(t, b) (например, при ЧМ, ФМ, ФИМ) является нелинейной функцией передаваемого сообщения и уравнение наблюдения становится нелинейным. Может быть нелинейным и уравнение состояния. Основополагающие результаты по теории нелинейной фильтрации, из которой, в частности, следуют и результаты линейной теории, получены Р. Л. Стратановичем. Дальнейшее развитие эта теория получила в работах В. И. Тихонова, Н. К. Кульмана, Ю. Г. Сосулина и многих других советских авторов [15, 16]. В настоящее время теория нелинейной фильтрации наиболее разработана для двух случаев: сообщение b(t) моделируется нормальным случайным процессом, сообщение b(t) представляет собой марковский процесс. Здесь остановимся лишь на теории фильтрации одномерных марковских гауссовских процессов, порождаемых линейным дифференциальным уравнением. Для этого частного случая уравнение наблюдения задано в виде

где s(t, b) - нелинейная функция b(t), а уравнение состояния - в виде (7.67). Как и в предыдущем случае, шум n(t) считается белым гауссовским с нулевым средним значением и односторонней спектральной плотностью N₀.

Не нарушая общности в уравнении (7.67), можно положить N₁ = 4α. Тогда b(t) будет нормированным безразмерным процессом, с единичной дисперсией (мощностью), а изменения глубины модуляции того или иного параметра скажутся лишь на коэффициенте (индексе) модуляции.

Поскольку процесс, описываемый стохастическим уравнением (7.67), является марковским (диффузионным), изменения во времени его плотности вероятности w(b, t) определяются уравнением Колмогорова - Фокера - Планка (2.30), которое в данном случае имеет вид

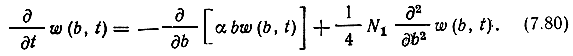
Для большей общности будем рассматривать передачу сигнала в канале с флуктуирующей фазой φ(t), которую представим процессом с независимыми приращениями, описываемым дифференциальным уравнением

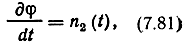
где n₂(t) - белый гауссовский шум с нулевым средним значением и односторонней спектральной плотностью мощности N₂. Все белые шумы, фигурирующие данной задаче, взаимно-независимы.

Располагая этими априорными данными, нужно найти устройство, которое с наименьшей погрешностью воспроизводило изменяющееся во времени случайное колебание b(t).

Если в качестве критерия оптимальности используется критерий среднеквадратической ошибки

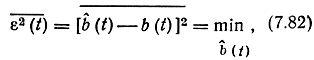
то, как известно (см. § 7.2), оптимальной оценкой является математическое ожидание апостериорного распределения

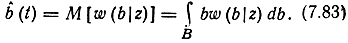
При этом погрешность оценки можно характеризовать апостериорной дисперсией

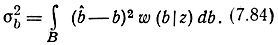
Таким образом, для вычисления оптимальной оценки и ее погрешности необходимо знать плотность апостериорного распределения w(b/z)y которая согласно формуле Байеса (7.6) определяется двумя множителями w(b) и w(z/b) (см. (7.20)). Плотность вероятности w(b) фильтруемого процесса b(t), удовлетворяющего (7.67), определяется из (7.80). Условная плотность вероятности w(z/b) (функция правдоподобия) легко находится из уравнения наблюдения (7.79). Так как сигнал s(t, b) является известной функцией аргументов t я b, а шум имеет нормальное распределение, то и w(z/b) также будет нормальным. При этом оценка b̂(t) является оптимальной не только по критерию минимума среднеквадратической ошибки, но и по критерию максимума апостериорной вероятности.

Апостериорная вероятность содержит всю информацию о передаваемом сообщении b(t), которую можно извлечь из наблюдаемого сигнала Z(t) на интервале (0, Т) и априорных сведений о b(t). В работах Р. Л. Стратановича показано, что апостериорная плотность вероятности w(z/b) реализации b(t) в конечный момент времени наблюдения определяется следующим нелинейным дифференциальным уравнением [15, 16]:

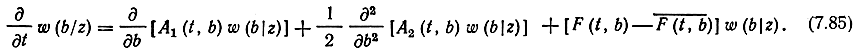
Здесь A₁ и A₂ - соответственно коэффициенты сноса и диффузии; F(t, b) - производная по времени от логарифма функции правдоподобия:

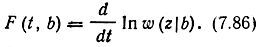
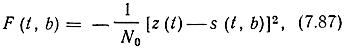
а применительно к не энергетическим параметрам сигнала (например, для частоты и фазы)

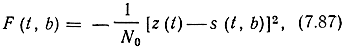
Уравнение (7.85) определяет полную процедуру фильтрации сообщения на фоне белого шума. Оптимальное приемное устройство должно моделировать уравнение (7.85) и определять оценку b̂(t), соответствующую максимуму апостериорной вероятности. В общем случае аналитическое решение этого уравнения оказывается трудной задачей. Схемы оптимального приемника при этом весьма сложные. Для получения более простых схем целесообразно использовать приближенные решения. При достаточно больших отношениях сигнал - шум и большом времени наблюдения есть основания считать, что апостериорная плотность вероятности приближенно нормальная:

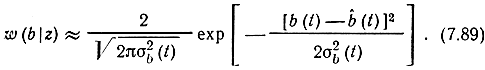
Такую аппроксимацию w(b|z) в теории нелинейной фильтрации принято называть гауссовским приближением, а получающийся при этом алгоритм обработки колебания z(t) - квазиоптимальным. Решение задачи -в этом случае существенно упрощается, так как апостериорная плотность вероятности (7.89) определяется всего двумя параметрами: средним значением b̂(t), определяющим оптимальную оценку передаваемого сообщения b(t), и дисперсией σ²_b(t), характеризующей ошибку фильтрации.

Если считать коэффициент сноса A₁(b, t) линейной функцией b, а коэффициент диффузии A₂(b, t) = const, то после подстановки (7.89) в (7.85) и несложных вычислений получим для определения b̂(t) и σ²_b(t) = k(t) систему из двух обыкновенных нелинейных дифференциальных уравнений:

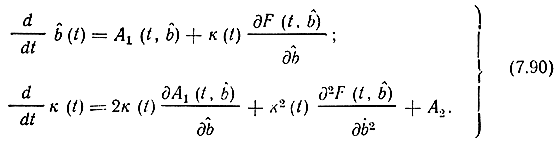
Таким образом, задача оптимальной фильтрации в гауссовском приближении сводится к совместному решению или моделированию уравнений (7.90). Система, моделирующая эти уравнения (нелинейный фильтр), будет воспроизводить переданное сообщение b(t) с минимальной среднеквадратической ошибкой (по крайней мере, в случае слабых помех, когда оправдано гауссово приближение) .

Для марковского гауссовского процесса, описываемого стохастическим дифференциальным уравнением (7.67)

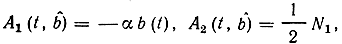
уравнения (7.90) запишутся так:

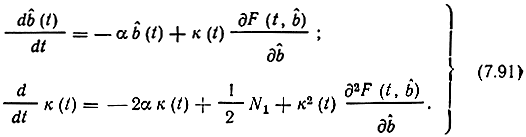
Если сигнал s(t, b) - b(t)f (t) линейно зависит от передаваемого сообщения b(t), то согласно (7.87)

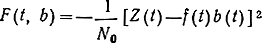
и уравнения (7.91) переходят в уравнения (7.71), (7.72), - описывающие линейный оптимальный фильтр Калмана.

Рассмотренная теория нелинейной фильтрации может быть обобщена и на случай, когда передаваемое сообщение описывается не гауссовским марковским процессом. В этом случае вместо уравнения (7.67) фигурирует нелинейное стохастическое дифференциальное уравнение.

Другим обобщением является передача сигнала, модулированного сообщением b(t), которое можно аппроксимировать компонентой многомерного марковского процесса [26].

В качестве примера рассмотрим применение теории нелинейной фильтрации для синтеза оптимальных приемников в системах с фазовой и частотной модуляцией.

Сигнал при фазовой модуляции

где u₀ и ω₀ - априорно известные значения амплитуды и частоты; β(t) - индекс фазовой модуляции; φ(t) - процесс, описывающий флуктуацию начальной фазы; B(t) положим нормированным марковским гауссовским процессом.

Для нахождения уравнения оценки определим функцию F(t, b̂). Согласно (7.88)

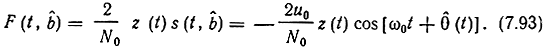
Запишем уравнение оценки, полагая вначале, что флуктуации начальной фазы отсутствуют: φ(t) = φ₀. Подставляя (7.93) в уравнение (7.91), получим

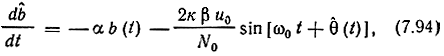
где θ(t) = βb̂(t) + φ₀.

Построим структурную схему фильтра, выделяющего из наблюдаемого колебания z(t) оптимальную оценку b̂(t). Для этого обозначим

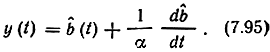
и перепишем (7.94) в виде

Легко убедиться, что если подать напряжение y(t) на интегрирующую цепь RC, где RC = 1/α, то напряжение на конденсаторе будет равно b̂(t). Для того чтобы сформировать напряжение y(t), достаточно иметь автогенератор на частоту f₀, модулируемый по фазе сигналом b̂(t) с индексом модуляции β и перемножител, осуществляющий умножение напряжения автогенератора на вход\ ное колебание z(t). Амплитуда автогенератора U_Γ = 2kβu₀/(αN₀). Коэффициент k определяют решением нелинейного дифференциального уравнения (7.91). В данном случае для установившегося режима

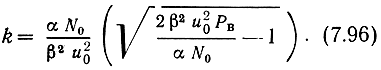
Таким образом, получаем один из возможных вариантов схемы для получения оптимальной оценки b(t), изображенный на рис. 7.10. Здесь ПГ - подстраиваемый генератор, фаза которого модулируется с помощью управляющего элемента (УЭ). Это не что иное, как схема автоподстройки фазы автогенератора по входному колебанию z(t). Благодаря этому она обладает в известной степени свойствами саморегулирования, в частности, мало чувствительна к точности установки начальной фазы φ₀ автогенератора и его амплитуды. Однако если начальная фаза φ подвержена значительным (по величине и скорости) флуктуациям, схема рис. 7.10 становится далеко не оптимальной.

Чтобы исследовать случай с "блуждающей" фазой φ(t) подчиняющейся

уравнению (7.81), учтем, что теперь в (7.94) θ̂(t) = βb̂ + φ̂(t). Теперь можно записать уравнение (7.91) для совместной оценки B̂(t) и θ(t):

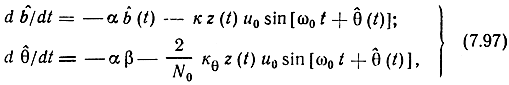
где k₀ - коэффициент, пропорциональный апостериорной дисперсии оценки фазы, определяемый дифференциальным уравнением, которое здесь не приводится. Отметим лишь, что он зависит от спектральной плотности белого шума n₂(t) входящей в определение процесса φ(t) (7.81), а также от спектральной плотности аддитивного шума n(t).

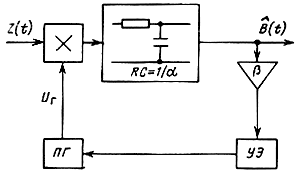
Рис. 7.10. Структурная схема оптимального демодулятора ФМ сигнала с постоянной фазой

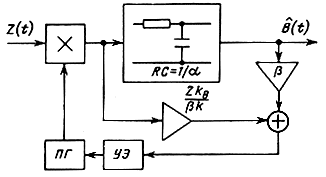
Рис. 7.11. Структурная схема оптимального демодулятора ФМ сигнала с блуждающей фазой

В этом случае в схеме фильтра на фазовый модулятор поступает помимо оценки сообщения b̂(t), также оценка флуктуирующей начальной фазы φ̂(t) [(рис. 7.11).

При частотной модуляции в (7.92)

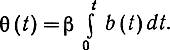
В остальном характер всех соотношений сохраняется. Схемы оптимального нелинейного фильтра по структуре такие же, как и для фазовой модуляции, - рис. 7.10 (при постоянной начальной фазе) и рис. 7.11 (при флуктуирующей начальной фазе). Отличие заключается в том, что в подстраиваемом генераторе модулируется не фаза, а частота. Несколько отличаются также коэффициенты усиления. Эти фильтры представляют собой схемы фазовой автоподстройки частоты (ФАПЧ). Заметим, что они аналогичны схеме рис. 7.2.

Аналогично определяют схемы оптимальной нелинейной фильтрации для других видов модуляции и для более сложных каналов. Так, например, для ЧМ в канале с рэлеевскими замираниями синтезирован фильтр, основой которой является схема рис. 7.11, но с добавлением цепи автоматической регулировки усиления (АРУ), работающей так, что осуществляются подавление "слабого" сигнала и большое усиление сильного. Расчет показывает, что средняя ошибка фильтрации при этом такая же, как и в отсутствие замираний.

Вопросы к главе 7

1. Как количественно оценивается помехоустойчивость при передаче непрерывных сообщений?
2. Покажите, что при большом отношении сигнал-шум критерий максимума правдоподобия совпадает с критерием минимума среднеквадратической ошибки.
3. Покажите, что оптимальным по максимуму правдоподобия приемником непрерывных сообщений может быть следящий приемник.
4. Сформулируйте условие оптимального приема непрерывных сообщений и поясните его геометрически.
5. Нарисуйте структурную схему следящего демодулятора и поясните принцип его работы.
6. Сравните выражения (7.37) и (7.41) для энергетического спектра помех на выходе оптимального приемника при AM и ЧМ. Изобразите графики спектров и покажите, что мощность шума на выходе приемника в полосе F_c при ЧМ будет существенно меньше, чем при AM.
7. Чему равен выигрыш при ЧМ? За счет чего достигается большое значение выигрыша при ЧМ и ФМ? Почему для ОМ он равен единице?
8. Чем объяснить увеличение выигрыша при ОМ и БМ по сравнению с AM?
9. Что такое аномальные ошибки и как они проявляются при передаче непрерывных сообщений?
10. Как объяснить пороговый эффект в широкополосных системах? Почему он отсутствует при ОМ?
11. При каком способе приема ЧМ сигналов достигается предельное (минимальное) значение порога?
12. Чему равен выигрыш при ФИМ-АМ? Сравните его с выигрышем для ЧМ.
13. Как определяется выигрыш и обобщенный выигрыш в системах с двойной модуляцией?
14. Проанализируйте амплитудно-частотную характеристику (7.64) оптимального фильтра, когда спектры сигнала и помехи частично или полностью перекрываются.
15. Для каких сигналов и помех достаточно линейной фильтрации для получения минимума среднеквадратической ошибки?
16. Можно ли уменьшить ошибку при линейной оптимальной фильтрации, если применить предыскажение сигнала в передатчике и соответствующее корректирование в приемнике?
17. * Фильтр Колмогорова-Винера и фильтр Калмана являются оптимальными по одному и тому же критерию min ε̄². В чем же различие между ними?
18. В чем различие подходов Колмогорова-Винера и Калмана в теории оптимальной линейной фильтрации?
19. * Как реализуется фильтр Калмана для гауссовского сообщения?
20. Для каких сигналов синхронный детектор является оптимальным демодулятором?
21. В чем сущность теории нелинейной фильтрации непрерывных сообщений? Какой критерий и какой метод синтеза оптимального нелинейного фильтра при этом используются?
22. Чем отличается структура оптимального нелинейного фильтра (демодулятора) при ФМ и ЧМ?
23. Поясните разницу в постановке задачи при построении согласованного фильтра (см. гл. 6) и оптимальных линейных фильтров (Колмогорова-Винера или Калмана).