7.7. Оптимальная линейная фильтрация непрерывных сообщении. Фильтр Калмана

Из предыдущего параграфа следует, что фильтр Колмогорова - Винера является оптимальным для выделения (оценки) стационарного сигнала. Модулированные же сигналы имеют конечную длительность и не являются стационарными.

На основе метода переменных состояний (см. § 3.5) возможен другой подход, при котором определяют не сами характеристики оптимального фильтра, а дифференциальные уравнения, моделирующие этот фильтр. В теории нелинейной фильтрации такой подход был применен P. JI. Стратановичем (1959 г.), а в теории линейной фильтрации Калманом и Бьюси (1960 г.). Метод дифференциальных уравнений позволяет решить более общую задачу- выделения с наименьшей погрешностью

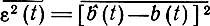
сообщения b (t) из наблюдаемого на конечном интервале времени сигнала z(t) = s(t, b)+ n(t). Условие стационарности сигнала и помехи в рамках этого метода не является обязательным. Относительно фильтруемого сообщения b(t) дополнительно предполагают, что оно порождается линейным стохастическим дифференциальным уравнением. В частном случае используют уравнение

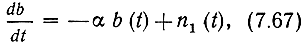
где n₁(t) - нормальный белый шум (порождающий процесс) с нулевым средним значением

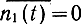
и односторонней спектральной плотностью N₁. Физически это означает, что сообщение b(t) рассматривают как результат прохождения стационарного белого шума n₁(t) через линейную цепь, в данном случае через интегрирующую цепочку RC. Для такой цепи постоянная α=1f(RC). Сформированное таким образом сообщение b(t) является гауссовским марковским процессом^* с функцией корреляции

^* (Реальные сообщения, как правило, не являются марковскими, поскольку зависимость между их отдельными сечениями более сложная. Тем не менее, марковская аппроксимация описывает реальное сообщение лучше, чем аппроксимация процессом с финитным спектром, у которого сечения, разделенные котельниковским интервалом, вовсе не коррелированы.)

Спектральная плотность мощности такого сообщения

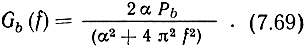
В более общем случае сообщение описывается системой линейных дифференциальных уравнений. Большой практический интерес представляет тот факт, что методы дифференциальных уравнений позволяют синтезировать оптимальный фильтр рекуррентным способом, обеспечивая удобство его реализации при использовании современных ЭВМ или микропроцессоров.

Рассмотрим случай линейной фильтрации, когда наблюдаемый процесс на входе фильтра задан уравнением

а сообщение b(t) - уравнением (7.67). Здесь f(t) - известная функция (несущее колебание); b (t)f(t) = s(t, b) - передаваемый сигнал; n(t) - белый гауссовский шум (не обязательно стационарный) с нулевым средним значением

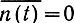
и односторонней спектральной плотностью N₀. Уравнение (7.70) является уравнением наблюдения, а (7.67) - уравнением состояния. Для получения уравнений фильтрации можно, как и в § 7.6, исходить из условия оптимальной линейной фильтрации (7.60). На основе этого условия выводится рекуррентное соотношение, которое позволяет получить следующие уравнения [15]:

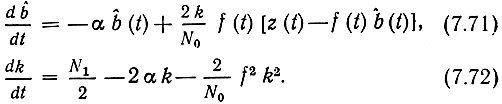
Уравнения (7.71) и (7.72) принято называть уравнениями фильтра Калмана. Уравнение (7.71) определяет алгоритм формирования оценки, а следовательно, и структурную схему фильтра, а (7.72) - ошибку фильтрации

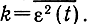
Структурная схема, моделирующая уравнение (7.71), приведена на рис. 7.8,а. Построение схемы удобно начинать с интегратора. Для этого обозначим правую часть (7.71) через y₁ (f) = y₁ (t) + y₂(t), где yi

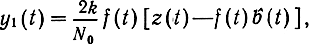
Тогда уравнение (7.71) N о

запишется как db̂/dt = y(t). Отсюда следует, что если на вход интегратора подать напряжение y(t), то на его выходе получим оценку сообщения b̂(t). Для того чтобы сформировать напряжение y₁(t), необходимо иметь генератор Г несущего колебания f(t), два перемножителя, сумматор и усилитель с коэффициентом усиления 2k/N₀. С помощью этих устройств осуществляются все операции, входящие в выражение для y₁(t). Напряжение y₂ (t) получается с помощью усилителя с коэффициентом усиления а, на вход которого поступает напряжение оценки b̂(t). Суммарное напряжение y(t) = y₁(t) + y₂(t) с выхода сумматора поступает на вход интегратора, выход которого представляет оценку b̂(t). Для немодулированного сигнала, когда s(t, b) = b(t) в (7.71) и (7.72) нужно положить f(t) = 1 и схема фильтра Калмана примет более простой вид (рис. 7.8,6).

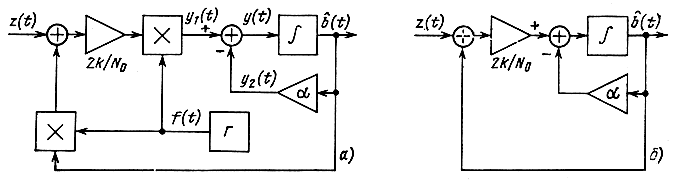
Рис. 7.8. Реализация фильтра Калмана для гауссовского сообщения при линейной модуляции (а) и при отсутствии модуляции (б) сигнала

В качестве примера рассмотрим фильтрацию гауссовского марковского сообщения в канале с амплитудной модуляцией, когда для передачи сообщения b(t), заданного (7.67), используется сигнал

Это сигнал AM с подавленной несущей. Уравнение наблюдения в этом случае, согласно (7.70),

Уравнение оценки согласно (7.71)

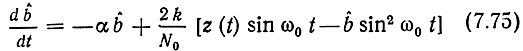
или

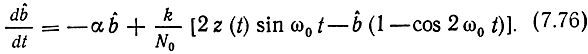
Практически период колебания несущей T = 2π/ω₀<<τ_к = 1/α, т. е. α<<ω₀, где τ_к - интервал корреляции сообщения b(t). При этих условиях слагаемым, пропорциональным cos 2ω₀t, можно пренебречь. Тогда имеем

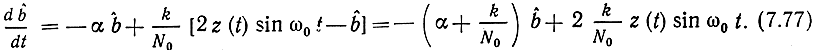
Уравнение (7.77) можно моделировать линейным фильтром разомкнутого типа (рис. 7.9) с постоянной времени RC = 1/(α + k/N₀). Постоянная k, равная ошибке фильтрации, определяется из уравнения (7.72). Как видим, оптимальный фильтр (демодулятор) для сигналов (7.73) представляет собой схему когерентного (синхронного) детектора с интегрирующим фильтром RC. В случае обычной амплитудной модуляции с несущей, когда s(t, b) = = u₀[1 + mb(t)]sin ω₀t, синхронный детектор выделяет огибающую [u₀ + mu₀b̂(t)] и поэтому для получения на выходе оценки сообщения b̂(t) ,в схему включены разделительный конденсатор С₁ устраняющий постоянную составляющую u₀, и аттенюатор А с коэффициентом затухания 1/(mu₀). Для не модулированного сигнала, когда f(t) = 1 и s(t) = b(t) уравнение оценки (7.76) принимает вид

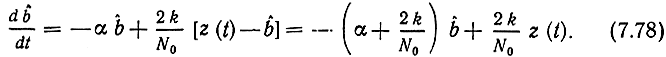
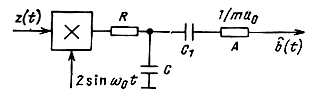
Рис. 7.9. Структурная схема оптимального демодулятора AM сигналов

Это уравнение моделируется интегрирующим фильтром с постоянной времени RC = /(α + 2k/N₀) и усилителем с коэффициентом усиления 2k/No. Можно показать, что в этом случае, когда сигнал s(t) и шум n(t) стационарны, фильтр Калмана совершенно эквивалентен фильтру Колмогорова - Винера. Однако для решения многих практических задач обработки сигналов и, в частности, данных телеизмерений, фильтры Калмана по вычислительной структуре оказались более удобными, чем фильтры Колмогорова - Винера.