7.6. Оптимальная линейная фильтрация непрерывных сигналов. Фильтр Колмогорова-Винера

Линейную фильтрацию широко используют в системах передачи информации для обработки сигналов, несмотря на то, что во многих случаях необходима нелинейная обработка. Объясняется это прежде всего простотой реализации линейных фильтров, которые сравнительно легко синтезируются и существованием развитой теории их построения, чего нельзя сказать о нелинейных фильтрах.

Линейные фильтры являются неотъемлемой частью любого приемного устройства. С их помощью осуществляется как додетекторная, так и последетекторная обработки сигналов. С помощью линейных фильтров сигналы разделяются в многоканальных системах передачи. Требования к этим фильтрам могут быть весьма различными в зависимости от их назначения. Здесь рассмотрим теорию оптимальной линейной фильтрации.

Пусть сигнал на входе линейного фильтра с импульсной реакцией g(t) представляет сумму переданного сигнала s(t) и помехи n(t)

Требуется найти такую функцию g(t)y которая минимизирует средний квадрат ошибки

где s(t) -оценка сигнала на выходе фильтра. Здесь считаем, что время запаздывания сигнала s(t) в фильтре t₀ = 0, а среднее значение берется по ансамблям сигналов S и помех N. Будем полагать, что s(t) и n(t) - стационарные взаимно-некоррелированные процессы с известными энергетическими спектрами G_s(f) и G_N(f). В такой постановке задача была решена независимо друг от друга академиком А. Н. Колмогоровым (1939 г.) и Н. Винером (1942 г.) и поэтому оптимальный (в указанном смысле) линейный фильтр называют фильтром Колмогорова - Винера. Требование физической реализуемости фильтра, как известно, сводится

к тому, что импульсная реакция фильтра должна удовлетворять условию g(t)=0 для всех t<0. Это ограничение учитывается в записи

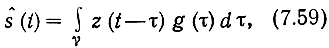
где область интегрирования γ для физически реализуемого фильтра есть интервал (0, ∞), а для не реализуемых фильтров - (-∞, ∞). Можно доказать, что необходимым и достаточным условием оптимальной линейной фильтрации является условие

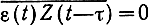(7.60)

для всех τ из γ.

Это означает, что фильтр нужно выбрать так, чтобы ошибка ε (t) = s (t) - S(t) была не коррелирована со входным сигналом Z(i) во все моменты времени в области γ. Если бы имела место корреляция между ошибкой и принимаемым сигналом, то при последующей обработке можно было бы получить лучшую оценку.

Докажем справедливость условия (7.60). Пусть g₁(t) - импульсная характеристика оптимального фильтра, удовлетворяющего условию (7.60), g₂(t)-импульсная характеристика любого другого линейного фильтра. Отклики фильтров соответственно обозначим через S₁(t) и S₂(t). Тогда

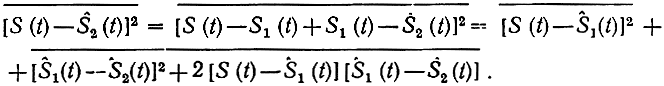
Поскольку функция S (t)- Ŝ₁ (t) = ε(t) удовлетворяет условию(7.60), то

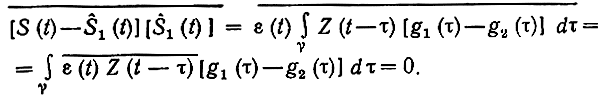
Следовательно,

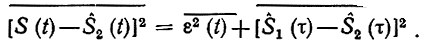
Очевидно, это выражение будет минимальным, когда Ŝ₂(t) = Ŝ₁(t), что и доказывает справедливость условия (7.60). Смысл этого условия состоит в том, что случайный вектор Ṡ должен быть строго ортогональной проекцией Ṡ на линейное подпространство, порождаемое случайным вектором z. Представим условие (7.60) в виде

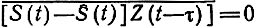
для всех τ из γ. Отсюда с учетом (7.59)

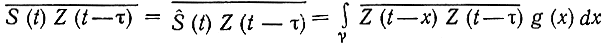
или

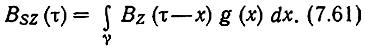
В том случае, когда сигнал S(t) и помеха n(t) некоррелированы,

(7.61) принимает вид

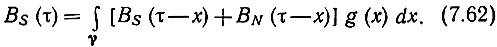
Это основное интегральное уравнение теории линейной фильтрации называется уравнением Винера - Хопфа. Его решением является искомая функция g(t), минимизирующая средний квадрат ошибки

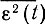
Не следует путать оптимальные линейные фильтры, определяемые (7.61) или (7.62) с согласованными фильтрами, рассмотренными в § 6.4. Если основное назначение рассматриваемых здесь фильтров состоит в наилучшем воспроизведении неизвестной формы сигнала, то задача согласованных фильтров заключается в формировании максимально возможного пика сигнала известной формы в момент отсчета на фоне шума.

Уравнение (7.62) легко решается для нереализуемых фильтров, т. е. когда γ=(-∞, ∞). Для этого случая, применив преобразование Фурье к обоим частям (7.62), получим в частотной области

Отсюда коэффициент передачи оптимального линейного фильтра

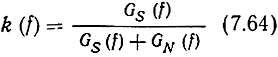
или в более общем случае, когда учитывается время запаздывания t₀ в фильтре,

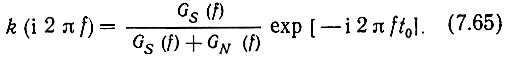
Ошибка при этом

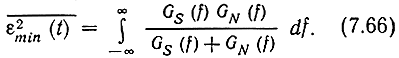
Легко заметить, что ошибка

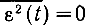
только в том случае, когда G_S(f)G_N(f) = 0, т. е. когда спектры сигнала и помехи не перекрываются. Во всех других случаях оптимальный фильтр пропускает различные частоты с тем меньшим весом, чем больше отношение G_N(f)/G_S(f) при данной частоте.

Увеличивая время запаздывания t₀, можно приблизиться к (7.66) и в случае реализуемого фильтра. Задача существенно усложняется, когда требуется, чтобы оптимальный фильтр k(f) был реализуем без существенного запаздывания. Для получения передаточной функции k(f) реализуемого фильтра используют полученное выше решение для γ=(-∞, ∞). С этой целью не реализуемый фильтр (7.65) раскладывают на несколько фильтров и выделяют из него оптимальную реализуемую часть [19]. В общем случае оптимальным по критерию минимума среднеквадратической ошибки является нелинейный фильтр. Исключение представляет случай, когда сигнал и помеха гауссовские, так как для них оптимальный фильтр всегда линеен.

Результаты оптимальной фильтрации можно существенно улучшить, если применить так называемое предыскажение сигнала с последующей его коррекцией на приеме. Сущность метода предыскажения состоит в том, что на передающей стороне сигнал s(t) пропускается через фильтр с коэффициентом передачи k₁ (f). Полученный таким образом видоизмененный сигнал s'(i) передается по каналу. На приемной стороне включен другой фильтр k₂(f). Характеристики фильтров k₁(f) и k₂{f) выбираются так, чтобы обеспечить минимум среднеквадратической ошибки. Расчеты показывают, что предыскажение дает тем больший выигрыш, чем меньше относительная ширина полосы перекрытия спектров сигнала и помехи. Предыскажение позволяет перераспределить мощность полезного сигнала в полосе частот канала так, чтобы обеспечить лучшие условия согласования источника сигнала с каналом (в общем случае полезно стремиться к тому, чтобы сумма спектральных плотностей мощности сигнала и мощности помехи была постоянной в пределах полосы частот канала). Это означает, что предыскажение можно рассматривать как "линейное кодирование" непрерывного сигнала, позволяющее уменьшить ошибку и улучшить использование пропускной способности канала.

Линейное предыскажение широко используется в современных системах связи. Характерными в этом отношении являются системы, в которых используется частотная модуляция. Согласно (7.41) плотность мощности шума на выходе ЧМ демодулятора увеличивается пропорционально квадрату частоты, так что верхние частотные составляющие сообщения подвержены шумам сильнее, чем нижние. Метод предыскажения и последующие коррекции позволяет снизить шум на верхних частотах и тем создать примерно одинаковые условия для передачи как нижних, так и верхних частот сообщения.

Следует отметить, что в результате предыскажений формируется новый сигнал с необходимыми свойствами. Так, например, в радиовещании и многоканальной радиорелейной и спутниковой связи с частотной модуляцией несущей используется предыскажение, близкое к дифференцированию. В этом случае на вход частотного модулятора поступает не первичный сигнал b(t), как это делается при ЧМ без искажений, а его производная db/dt. Поэтому пропорционально b(t) изменяется не мгновенная частота, а мгновенная начальная фаза несущего колебания, т. е. формируется не ЧМ, а ФМ сигнал. Так как спектр шума на выходе демодулятора ФМ сигнала равномерный (7.39), то тем самым в многоканальных системах обеспечивается одинаковая помехоустойчивость во всех частотных каналах, а в случае радиовещания - более качественное воспроизведение речевых и музыкальных передач [17}.