
7.5. Порог помехоустойчивости. Аномальные ошибки
Все широкополосные системы модуляции обеспечивают высокую помехоустойчивость при условии, что отношение сигнала к помехе ρвх па входе приемника больше некоторого предельного (порогового) значения ρпр. При ρвх<ρпр широкополосные системы теряют свои преимущества (резко снижается помехоустойчивость) и связь становится практически невозможной. Значение порога определяет предельную дальность связи при заданной мощности передатчика. Поэтому важно определить это значение и установить закон изменения отношения сигнала к помехе на выходе приемника за порогом (ρвх<ρпр).
Рассмотрим, как объясняется пороговый эффект теорией информации. Обратимся вновь к выражению (7.4) для обобщенного выигрыша, выразив его в децибелах:
g'[ДБ] (ρвых)[ДБ] (ρвхα)[ДБ]. (7.52)
Заметим, что
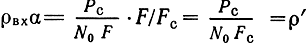
есть отношение мощности сигнала на входе приемника к мощности той части шума, которая лежит в полосе частот, равной ширине спектра сообщения Fс (а не в полосе спектра сигнала F). Равенство Fс и F имеет место при непосредственной передаче, а также при однополосной модуляции.
Если для некоторой системы связи построена зависимость ρвых от ρ'вх в децибелах, то для любого значения ρвых обобщенный выигрыш g', получается путем измерения разности ординат данной кривой и прямой, проведенной под углом 45° (рис. 7.5). В идеальной системе согласно (7.35)
lg ρвых = αlg(1+ρвх) (7.53)
или для случая, когда ρвх>>1,
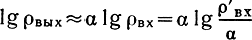
ρвых [ДБ] = α (ρвх[дБ] - α[ДБ])(7.54)
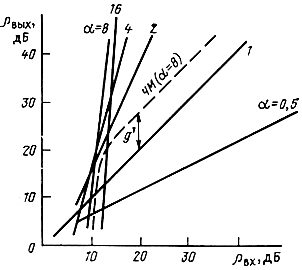
Рис. 7.5. Зависимость ρвых от ρ'вх для идеальной системы связи
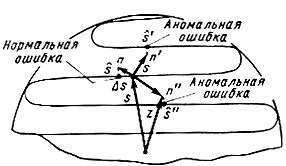
Рис. 7.6. Геометрическая трактовка появления аномальных ошибок
Это не что иное, как семейство прямых. На рис. 7.5 они изображены сплошными линиями. Для α=1 прямая проходит через начало координат под углом 45°; для α>1 эти прямые идут круче и пересекают ось абсцисс правее начала координат. Из (7.54) получаем обобщенный выигрыш в децибелах для идеальных систем, вычитая ρ'вх [ДБ] из ρвых [дБ]
gmax[дБ] (α-1) (ρвх[дБ] α[дБ]) (7.55)
Из выражения (7.55) следует, что в идеальной системе обобщенный выигрыш в логарифмическом масштабе растет линейно с увеличением ρ'вх. Как было показано в § 7.4, для реальных систем обобщенный выигрыш g' не зависит от ρвх, если ρвх>1. Тогда соответствующие им зависимости представляют собой прямые, параллельные прямой, проходящей через начало координат под углом 45°, но сдвинутые на величину g' (на рис. 7.5 одна из таких кривых изображена штриховой линией). Если бы кривые для реальных и идеальных систем пересекались, то это бы означало, что реальная система стала лучше идеальной. Очевидно, что это невозможно и кривые для реальных систем располагаются всегда не выше соответствующих кривых для идеальных систем. Отсюда можно сделать вывод, что системы, дающие выигрыш при больших ρвх, не могут сохранять его постоянным с уменьшением ρвх. Начиная с некоторого порогового значения этого отношения ρвх, выигрыш системы резко уменьшается. Более того, выигрыш может стать отрицательным (проигрышем), если ρ'вх<α. Чем больше α, тем сильнее сказывается пороговый эффект. Системы с α<1 вообще не подвержены пороговым явлениям, но они и при больших рвх не дают выигрыша. Зато они позволяют передавать сообщения по каналу с полосой пропускания, равной или меньшей ширины спектра сообщения. Для этого сообщения должно быть преобразовано в сигнал, спектр которого уже спектра сообщения. Чтобы получить высокую верность передачи в такой системе, необходимо иметь достаточно большое отношение мощности сигнала к мощности помехи в канале, поскольку при α<1ρвых<ρвх. На практике системы с α<1 применения пока не находят.
Поясним теперь явление порога геометрически. Для этого воспользуемся понятиями пространства сообщений и пространства сигналов, введенными в § 2.5. Каждому сигналу s(t) соответствует точка в n-мерном пространстве, где n =2TF - база сигнала, а ансамблю возможных сигналов - некоторая область в этом пространстве сигналов. При фиксированной мощности область возможных сигналов представляет собой гиперсферу с радиусом
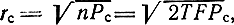
а область принятых колебаний Z(t) = S(t) + N (t)-сферу с радиусом
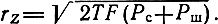
Вокруг каждой точки переданного сигнала образуется область неопределенности, обусловленная помехой. Если помехой является гауссовский шум, то эта область имеет сферическую форму с радиусом
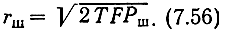
Как отмечалось, модуляция является отображением пространства сообщений на пространство сигналов, а демодуляция - обратным отображением пространства принятых сигналов в пространство принятых сообщений (оценок). В общем случае размерность (база) пространства сообщений 2FcT отличается от размерности пространства сигналов 2FT.
Рассмотрим некоторый отрезок прямой в области пространства возможных сообщений (эта область определяется, например, нормировкой сообщения). При модуляции этот отрезок отобразится в некоторую линию в пространстве сигналов, каждая точка S которой соответствует определенной реализации сообщения. Форма и длина этой линии зависят от вида модуляции. Помеха, наложившаяся на сигнал, вызовет смещение точки s в некоторую точку b̂ = b + Δb, соответствующую другому сообщению s = s + Δs аналогично тому, как было (показано на рис. 7.4. Очевидно, чем больше As/Ab, тем меньше ошибка в принятом сообщении при той же помехе.
Для увеличения помехоустойчивости (отношения As/Ab) необходимо увеличивать длину линии сигналов, соответствующей данному отрезку в пространстве сообщений. Это можно сделать, расширяя используемую область сигналов (радиус rс). Но поскольку мощность сигнала ограничена, для этого нужно увеличивать базу сигнала, расширяя его спектр. При этом линия сигнала может приобретать сложную извилистую форму.
На рис. 7.6 показан пример такой линии сигналов, причем для наглядности использовано двумерное пространство сигналов (при одномерном пространстве сообщений). Заметим, что при линейной модуляции линии сигнала и сообщений подобны и поэтому выигрыш в них невозможен. В случае широкополосных систем (например, ЧМ) линия сигналов имеет сложную извилистую форму. Длина линии увеличивается с увеличением полосы частот сигнала. Однако при ограниченной мощности сигнала это удлинение ведет к сближению различных витков линии сигнала. Пока помеха "мала" (например, n на рис. 7.6), точка принятого колебания z = s + n с большой вероятностью попадает в окрестность точки передаваемого сигнала s и воспроизводится сообщение b, соответствующее ближайшей точке s, находящейся на рассматриваемом витке линии сигнала. Сдвиг Δs вдоль линии сигнала мал и определяет нормальную ошибку Δb и соответственно
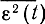
(7.2). Такие ошибки ухудшают лишь качество оценки сообщения. Сильная помеха (n' или n" на рис. 7.6) может перевести точку принимаемого колебания на другой виток линии сигнала (точки s' и s"). Такие "перескоки" связаны с появлением так называемых аномальных ошибок, которые не только ухудшают качество оценки сообщения, но делают ее совершенно ошибочной. Появление аномальных ошибок резко ухудшает помехоустойчивость связи и является причиной возникновения порога помехоустойчивости в широкополосных системах модуляции (ЧМ, ФМ, ФИМ и т. п.). Очевидно, в области порога помехоусточивость передачи непрерывных сообщений можно характеризовать вероятностью аномальных ошибок Ран (ошибок неоднозначности оценки). Можно сказать, что вероятность аномальной ошибки Ран определяет верность оценки сообщения, а среднеквадратическая ошибка
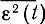
определяет точность (качество) этой оценки.
Вычисленные на основе более точной теории зависимости ρвых от ρвх для ОМ, AM и ЧМ представлены на рис. 7.7, из которого видно отсутствие порога при ОМ и зависимость порога при ЧМ от индекса модуляции. Существует оптимальное значение индекса модуляции, при котором для обеспечения заданной верности приема ρвых затрачивается минимальная мощность сигнала Pc min, равная пороговой мощности Рс.пр. Это значение тем больше, чем выше требуемая верность приема.
Полученные теоретические значения порога для различных видов модуляции являются предельными, которые в реальных приемниках могут быть достигнуты, но не могут быть превзойдены. По экспериментальным данным порог в системе ЧМ при обычном способе приема наступает примерно при равенстве пиковых значений сигнала и помехи, что соответствует ρвх, существенно выше теоретического. Это означает, что при большом уровне помех реальная помехоустойчивость приемника ЧМ значительно меньше потенциальной. Следовательно, имеется возможность усовершенствованием схемы приемника снизить порог помехоустойчивости и тем самым увеличить дальность связи при той же мощности передатчика. Эта задача особенно актуальна для спутниковых и космических систем связи.
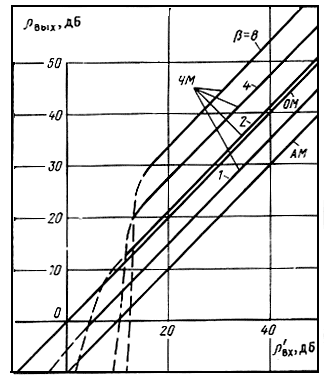
Рис. 1.1. Кривые помехоустойчивости для ЧМ (β = 1, 2, 4, 8), AM и ОМ
Для снижения порога при ЧМ применяют различные схемы следящих демодуляторов, в частности, схему с обратной связью по частоте, синхронно-фазовый демодулятор и демодулятор со следящем фильтром ([5]. Минимальный (предельный) порог помехоустойчивости достигается в схеме оптимального демодулятора (см. § 7.8).

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
