7.4. Помехоустойчивость систем передачи непрерывных сообщений при слабых помехах

Для передачи непрерывных сообщений по каналу связи применяют различные виды модуляции. При синусоидальном переносчике на практике используют амплитудную модуляцию (AM), балансную модуляцию (БМ), однополосную модуляцию (ОМ), фазовую модуляцию (ФМ) и частотную модуляцию (ЧМ). Определим потенциальную и реальную помехоустойчивость этих систем.

Амплитудная модуляция формирует сигнал вида S(t, В) = u₀[1 + mB(t)]cos ω₀t, где m≤1. Тогда

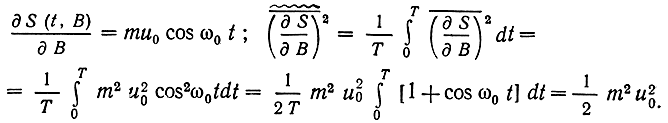
Согласно (7.28) энергетический спектр шума на выходе приемника AM

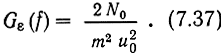
Мощность сигнала на входе приемника^*

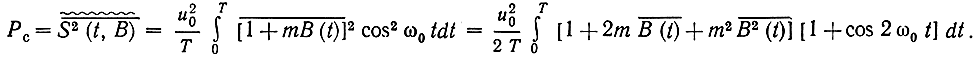
Поскольку сообщение - центрированный процесс,

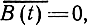
а вследствие принятой нормировки

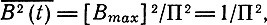
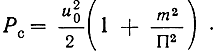
^* (Модулированный сигнал S(t) обычно является нестационарным процессом, и поэтому для нахождения его мощности необходимо усреднять квадрат сигнала по ансамблю и по времени.)

Здесь и далее полагаем, что ω₀T>>1 и поэтому значением

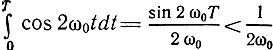
можно пренебречь по сравнению с Т.

На основании (7.32) с учетом, что при AM F = 2F_c, получаем следующие выражения для выигрыша и обобщенного выигрыша при оптимальном приеме:

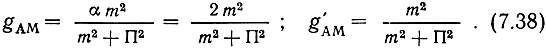
Предельное значение выигрыша при AM равно 1. Оно достигается тогда, когда m = 1 и Π = 1. Практически всегда m<1. 1, а Π>1, и поэтому g_AM<1 и g'_AM<0,5, т. е. система AM дает проигрыш. Так, при передаче речи Π≈3, и тогда при m = 0,9 g_АМ = 0,165 и g'_АМ = 0,083. Малые значения выигрыша при AM обусловлены тем, что лишь небольшая часть мощности сигнала заключена в боковых полосах, несущих полезную информацию. Следовательно, устранение несущей в сигнале AM может привести к увеличению выигрыша, что и имеет место при балансной и однополосной модуляции.

При балансной модуляции (AM с подавленной несущей) сигнал формируется путем простого перемножения первичного сигнала В (t) и колебания переносчика u⁰cosω_0t

Средняя мощность такого сигнала

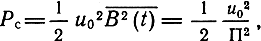
а

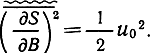
С учетом этих соотношений имеем (при α = 2), g_БМ = 2, g'_БМ= 1. Отсюда, выигрыш при БМ не зависит от пик-фактора сообщения.

Однополосная модуляция, как известно, представляет собой просто перенос спектра первичного сигнала вверх на частоту ω₀. Это линейная операция, при которой не изменяется ширина спектра, а также соотношения между мощностями составляющих. Поэтому при демодуляции входная помеха преобразуется в выходную таким же образом, как и сигнал. Из этих соображений можно, не прибегая к громоздким вычислениям, записать: g_ОМ = g'_ОМ = 1. Таким образом, обобщенный выигрыш при БМ и ОМ одинаков. Однако полоса частот, занимаемая сигналом при ОМ, в 2 раза меньше, чем при БМ.

Системы AM, БМ и ОМ - линейные, поэтому полученные выше соотношения для оптимального приемника справедливы как при слабых, так и при сильных помехах на входе. Эти соотношения определяют предельную (потенциальную) помехоустойчивость систем.

Выясним, реализуется ли эта помехоустойчивость при обычных способах приема, используемых в реальных приемниках. Для этого рассмотрим прием ДМ сигналов при амплитудном (линейном) и синхронном детектировании. Перед детектором обычно включают фильтр, пропускающий частоты сигнала. Шум на выходе такого фильтра представляет собой узкополосный процесс, который можно записать согласно (2.72) в виде N(t) = N_c (t) cos ω₀t - N_s(t) sin ω₀t, где N_c(t) и N_s(t)-гауссовские процессы со спектральной плотностью 2N₀ в полосе частот от 0 до F/2 (см. примечание на с. 50). Тогда принимаемое колебание на входе детектора

Огибающая этого колебания

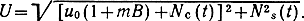
При слабой помехе квадратурной составляющей шума N_s(t) можно пренебречь, и тогда U≈[1 + mB(t) + N_c (t)]. Если в приемнике применен обычный линейный детектор огибающей, то переменная составляющая колебания на его выходе k[mu₀B(t) + N_c(t)], где k - коэффициент передачи детектора.

При синхронном детектировании приемник реагирует лишь на косинусоидальную составляющую подаваемого на детектор колебания Z(t) и поэтому тот же результат будет точен не только при слабой, но и при сильной помехе. Если усиление приемника подобрано так, что в отсутствие шума колебание его на выходе равно первичному сигналу B(t), то при наличии помехи оно будет

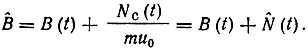
Шум на выходе приемника N̂(t) = N_с (t)/(mu₀) является нормальным флуктуационным колебанием с нулевым средним значением. Энергетический спектр этого колебания

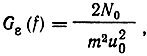
что совпадает с выражением (7.37). Таким образом, обычный приемник с синхронным детектором реализует потенциальную помехоустойчивость при любом уровне помех на входе, а приемник с линейным детектором огибающей - только при их малом уровне.

Можно показать, что и при детектировании сигналов БМ и ОМ синхронным детектором потенциальная помехоустойчивость реализуется при любом уровне шума на входе приемника.

Фазовая модуляция также относится к прямым системам модуляции, однако к нелинейным. При фазовой модуляции сигнал можно записать в виде: S(t, В) = u₀ cos [ω₀t + βB(t)], где β - девиация фазы или индекс фазовой модуляции. Для такого сигнала

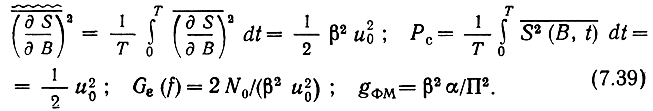
При больших индексах модуляции β ≈ α/2

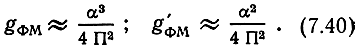
Как видно, при ФМ выигрыш зависит от индекса модуляции и пик-фактора сообщения. Так как β может быть больше единицы, то и выигрыш в этой системе можно получить значительно больше единицы. Платой за этот выигрыш является расширение полосы частот, занимаемой сигналом. Полученные соотношения справедливы для малого уровня шума на входе приемника, так как сигнал S(t, В) при ФМ нелинейно зависит от B (t).

Частотная модуляция относится к интегральным системам модуляции, потенциальная помехоустойчивость которой определяется на основании соотношения (7.29). Сигнал при ЧМ можно представить в виде S (t, В) = u₀ cos [ω₀t + Δωψ(t) ], где Δω - девиация частоты,

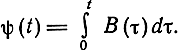
Для такого сигнала

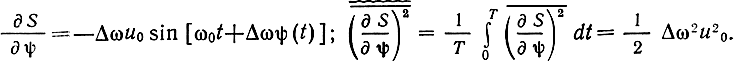
Тогда на основании (7.29) энергетический спектр шума на выходе приемника ЧМ

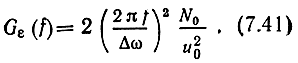
а на основании (7.32) получаем выражения для выигрыша:

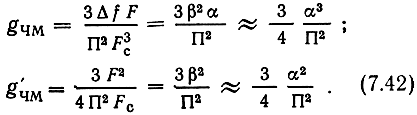
Здесь учтено, что при большом индексе модуляции β = Δf/F_c, а полоса сигнала F≈2βF_c. При ЧМ так же, как и при ФМ, выигрыш может быть значительно больше единицы, и достигается это за счет расширения полосы частот сигнала (увеличения индекса модуляции). Частотная и фазовая модуляция являются примерами систем, в которых верность передачи сообщений при данном уровне помех может быть повышена не только за счет увеличения мощности сигнала, как это имеет место при линейных видах модуляции, но и за счет расширения полосы частот, занимаемой сигналом. Все эти выводы и полученные выше соотношения для ЧМ, так же как и для ФМ, справедливы лишь при малом уровне помех. Эти системы, как будет показано, имеют ярко выраженный пороговый эффект.

Системы с поднесущими. В технике связи нередко применяют двойную модуляцию. При этом передаваемым сообщением (первичным сигналом) модулируется вспомогательное колебание (поднесущая) с частотой f_пн, а затем?

полученным модулированным колебанием модулируется другое колебание (несущая) с частотой f_п>>f_пн. В многоканальных системах двойная модуляция позволяет осуществить частотное разделение каналов.

В одноканальных системах с поднесущей двойная модуляция позволяет снизить требования к стабильности несущей частоты, заменив его более легко выполнимым требованием к стабильности поднесущей частоты. Кроме того, такие системы, как ЧМ-AM или ФМ-AM, применяют в тех случаях, когда нельзя использовать непосредственно ЧМ или ФМ из-за замираний. Так, например, в телеметрических системах необходимо передавать не только форму, но и масштаб сообщения B(t). Для этих целей нельзя в каналах с замиранием использовать AM или ОМ, так как замирания будут вызывать изменения амплитуды принимаемого сообщения. В таких случаях часто используют ЧМ-AM или ФМ-AM. По этой же причине система ЧМ-AM применяется в фототелеграфных системах на коротких волнах.

Разнообразие систем модуляции позволяет осуществить большое число систем с поднесущими. Практически применяют системы ОМ-AM, ФМ-AM, ЧМ-AM, ЧМ-ОМ, ОМ-ЧМ, ЧМ-ЧМ и др.

При малом уровне помех выигрыш систем с поднесущими определяется таким же методом, что и при обычной однократной модуляции с помощью формул (7.32). Рассмотрим для примера систему ФМ-AM. В этой системе сигнал

Так как система ФМ-AM относится к прямым системам модуляции, то выигрыш можно определить по формулам (7.32) с учетом выражения (7.28).

Для сигнала (7.43) имеем

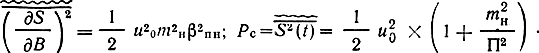
Тогда обобщенный выигрыш в системе ФМ-AM

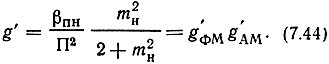
Из (7.44) следует, что обобщенный выигрыш равен произведению выигрышей при ФМ и AM. Легко убедиться, что для любой системы с поднесущей, в которой модуляция несущей является прямой, обобщенный выигрыш g' равен произведению выигрышей первой g'_ΠΗ и второй g'_Η ступеней модуляции, т. е. g' = g'_ΠΗg'_Η.

Системы с импульсной модуляцией. Согласно теореме Котельникова непрерывное колебание В (t) может быть передано по линии связи с необходимой точностью путем передачи его отдельных мгновенных значений

взятых для моментов времени, отстоящих друг от друга на величину T_i≤1/2F_c, где F_c- наивысшая частота, содержащаяся в колебании B(t).

В системах связи, основанных на этом принципе (импульсных системах), для передачи колебания В (t) используется периодическая последовательность импульсов

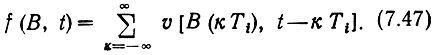
При этом один из параметров этой последовательности изменяется в соответствии с изменением мгновенных значений (7.45) передаваемого колебания В (t). Таким параметром может быть, например, амплитуда импульса, момент его прихода (фаза), его ширина и частота следования импульсов. Соответственно виды импульсной модуляции называются АИМ, ШИМ, ЧИМ.

Модулированная последовательность импульсов на выходе первой ступени модуляции

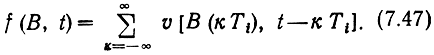
Здесь v (t)-огибающая импульса, причем v(t) = 0 при t<0 и t>τ₀ где τ₀ - длительность импульса.

Для передачи колебания f(B, t) по радио необходимо применить еще одну ступень модуляции. При этом может быть использована любая из систем модуляции, рассмотренных выше. Однако чаще всего во второй ступени модуляции модулированная последовательность импульсов f(B, t) перемножается с гармоническим напряжением несущей, в результате чего получается сигнал

Эту операцию перемножения называют амплитудной модуляцией и обозначают соответствующие системы сокращениями типа АИМ-АМ, ФИМ-АМ, ШИМ-АМ и т. д.

Из всех систем импульсной модуляции наиболее помехоустойчивыми являются ФИМ и ЧИМ. Так как первая из них несколько проще, то для передачи сигналов по каналам связи используется почти исключительно ФИМ-AM. Модуляцию АИМ и ШИМ в каналах связи практически не используют и применяют лишь в процессе обработки сигналов. Поэтому приведем только сведения о помехоустойчивости системы ФИМ-AM [5].

Обобщенный выигрыш в системе ФИМ-AM

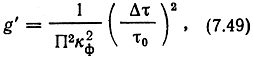
где k_ф - коэффициент, зависящий от формы импульса; Δτ - максимальная девиация положения импульса.

Как видим, помехоустойчивость системы ФИМ зависит от формы импульса. При оптимальном выборе параметров системы ФИМ-АМ: F_τ0≈1, f_i = 2F_c, Δτ = 1/(2f_i):

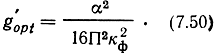
При k²_ф = 1/12, что соответствует треугольной форме импульсов,

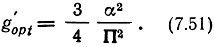
Это совпадает с (7.42) для системы с частотной модуляцией. Следовательно, потенциальная помехоустойчивость системы ФИМ-АМ при оптимальном выборе параметров и системы ЧМ при том же значении α одинакова.