7.3. Оптимальная демодуляция непрерывных сигналов

Определим условия оптимального приема непрерывных сообщений. Пусть сообщение представляет собой некоторый процесс (первичный сигнал) b(t). Он может непрерывно изменяться во времени и принимать любую форму.

Для простоты анализа будем считать, что функция b(t) принимает значения от +1 до -1, что реализации сообщения имеют конечную длительность Т, и что их спектр практически ограничен частотами от 0 до F_с. При этих условиях, согласно (2.98), функции b (t) могут быть разложены по ортонормированному базису φ_k(t) и представлены в виде усеченного ряда

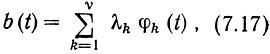
где λ_k - случайные коэффициенты, определяющие передаваемое сообщение. При разложении в тригонометрический ряд Фурье λ_k - составляющие спектра, а при разложении в ряд Котельникова- отсчетные значения b (kkt) функции b (t). Здесь Δt = - 1/(2F_c), ν = T/Δt = 2TF_c. Таким образом, при известной системе базисных функций φ_k(t) передача непрерывных сообщений b (t) эквивалентна передаче v значений коэффициентов (параметров) λ_k. Для (передачи каналу колебание b(t) преобразуется в сигнал S(t, b). Поскольку колебание (7.17) определяется параметрами λ_k (k = 1, 2, ....,ν), то и сигнал зависит от этих параметров. Принятый сигнал с учетом наложения помехи

Влияние помех приведет к тому, что каждый параметр λ_k будет принят с некоторой погрешностью Δλ_k. В результате оценка сообщения

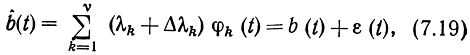
где

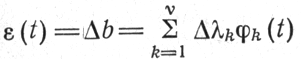
-погрешность воспроизведения сообщения b(t) (шум на выходе приемника).

Таким образом, задача оптимального приема непрерывного сообщения b (t) сводится к задаче совместного оптимального приема совокупности многих параметров λ = (λ₁, λ₂,..., λ_n). Эта задача является обобщением рассмотренной в § 7.2 задачи оптимальной оценки одного параметра.

Итак, по реализации z(t) необходимо восстановить переданное сообщение b (t) с возможно большей точностью, хотя бы при слабых помехах. Как было установлено для этого необходимо на основе анализа принятого колебания z(t) найти максимум в пространстве R_ν апостериорного распределения:

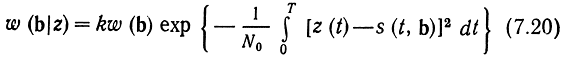
или при w(b) = const - минимум по b (t) интеграла

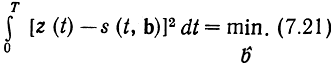
Следовательно, оптимальный приемник должен воспроизводить сообщение которое соответствует, как и при передаче дискретных сообщений, тому из возможных сигналов s(t, b̂), который меньше других отличается в среднеквадратическом смысле от реализации сигнала z(t) на входе приемника.

При отсутствии помех такой приемник воспроизводит сообщение без искажений (без ошибок): z(t) = s(t, b), b̂(t) = b(t) и ε̄²(t)=0, а при наличии помех ошибка минимальна.

Запишем (7.20) в другом виде, подобном (7.15):

где

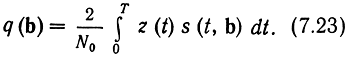
Отсюда следует, что при известной априорной вероятности определение апостериорной вероятности сводится к вычислению функции q(b), т. e. скалярного произведения принятого колебания z(t) на переданные (ожидаемые) сигналы s(t, b).

Во многих случаях для приближенного нахождения q(b) целесообразно применение простых следящих устройств. Рассмотрим принципиальную возможность построения таких устройств. Подробное и более строгое обоснование на основе теории нелинейной фильтрации приводится в § 7.8.

При передаче непрерывных сообщений сигнал s(t, b) не является полностью известным. Однако обычно имеется некоторая априорная информация об этом сигнале. Известны, например, несущая частота, вид модуляции, ширина спектра сигнала и т. п. Часть информации можно получить в результате наблюдения над принятой реализацией сигнала z(t) за предшествующий промежуток времени. В результате имеется возможность определить оценку сигнала s(t, ḃ) и вычислить функцию q(ḃ) для этой оценки:

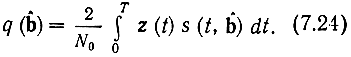
Функцию q (b̂) можно найти с помощью фильтра с переменными параметрами (рис. 7.1) или схемы следящего коррелятора (рис. 7.2). Каждая из этих схем имеет основной информационный канал, на выходе которого получается оценочное значение b̂(t) передаваемого сообщения и канал обратной связи, с помощью которого в схеме рис. 7.2 формируется опорный сигнал s(t, b̂), а в схеме рис. 7.1 с помощью управляющего элемента (УЭ) производится изменения параметров фильтра СФ так, чтобы он был согласован с непрерывно изменяющимся ожидаемым сигналом s(t, b̂). В схеме рис. 7.2 с помощью УЭ изменяется модулируемый параметр несущего колебания, формируемого генератором (Г). При частотной модуляции, например, этим параметром будет частота, при временной импульсной модуляции - сдвиг импульсов по времени и т. п. Фильтр нижних частот ФНЧ в этой схеме выполняет роль интегратора на интервале наблюдения T, который связан с максимальной частотой F_c в спектре передаваемого сообщения соотношением Т = 1/(2F_c).

Рассмотренные схемы являются квазиоптимальными, поскольку получаемая оценка s(t, ḃ) не является наилучшей возможной.

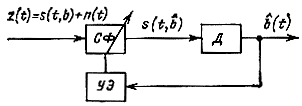
Рис. 7.1. Структурная схема демодулятора со следящим фильтром

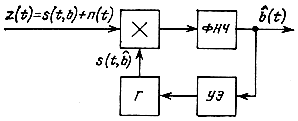
Рис. 7.2. Структурная схема следящего корреляционного демодулятора

При различных видах модуляции принцип следящего приема остается одним и тем же. Вид модуляции определяет параметр, за которым должно осуществляться слежение. Иначе говоря, оптимальный приемник должен с наименьшей ошибкой следить за передаваемым случайным колебанием b(t). Схемы следящего приема позволяют практически реализовать помехоустойчивость, близкую к потенциальной. При линейной модуляции, когда s(t, b) = f(t)b (t), где f(t)-известная функция (несущее колебание), оптимальный демодулятор можно реализовать разомкнутой схемой с синхронным детектором (рис. 7.3).

Перейдем к определению помехоустойчивости систем связи при оптимальном приеме. Заметим, что эту потенциальную помехоустойчивость можно вычислить, не уточняя структуры оптимального демодулятора. Для этого достаточно знать, что он выдает решение соответствующее максимуму (7.24).

Прежде чем приступить к выводу формул, определяющих потенциальную помехоустойчивость, напомним основные принципы классификации видов модуляции при передаче непрерывных сообщений. В общем случае модуляция заключается в том, что множество сообщений (первичных сигналов) B(t) преобразуется (отображается) в множество вторичных сигналов S(t) = S[t, B(t)]. Этой записью подчеркивается, что значение сигнала S в некоторый момент t₀ определяется в общем случае всем поведением сообщения В (t) на всей оси времени.

В частном случае, если сигнал S(t) в любой момент t₀ зависит не от всего хода сигнала В (t), а только от его значения в момент t₀, то система модуляции называется прямой. В этом случае сообщение b(t) входит непосредственно в выражение сигнала S(t). К прямым относится подавляющее большинство применяемых методов модуляции. Остальные системы модуляции, в которых S (t) зависит от общего поведения сигнала B(t), называются непрямыми. Среди них особый интерес представляют интегральные системы, в которых В (t) входит в выражение S(t) под интегралом.

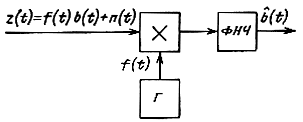
Рис. 7.3. Структурная схема демодулятора с синхронным детектором

Система модуляции называется линейной, если S(t) можно получить из B(t) с помощью линейных операций. Линейные системы могут быть прямыми (например, амплитудная - AM) и непрямыми (например, однополосная - ОМ).

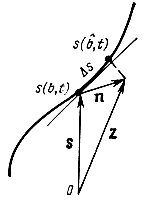
Рис. 7.4. Геометрическое представление сигнала и шума

Геометрически модуляцию можно рассматривать как отображение пространства сообщений В в пространство сигналов S, а демодуляцию - как обратное отображение. При демодуляции помеха n(t) на входе приемника отображается в погрешность оценки сообщения (шум воспроизведения или шум на выходе приемника) ε(t).

Рассмотрим прием непрерывного сообщения на фоне белого гауссовского шума n(t) со спектральной плотностью N₀. При достаточно слабом шуме погрешность ε(t) = b̂(t) - b(t) (шум на выходе приемника) представляет собой также гауссовский процесс со спектральной плотностью G_ε (f), которую и будем определять. Для этого удобно воспользоваться геометрическим представлением. В пространстве сигналов каждой реализации сигнала s(t, b) при различных b соответствует точка. Если s зависит непрерывно от b (что имеет место во всех аналоговых системах связи), то все эти точки образуют некоторую кривую (рис. 7.4). Принятый сигнал z(t) является также точкой в пространстве сигналов, как правило, не лежащей на кривой s(t, b). Максимально правдоподобная оценка b̂ соответствует тому сигналу s(t, b̂), который изображается на сигнальной кривой точкой, ближайшей к точке z. Обозначим Δs = s(t, b̂)-s(t, b), где b - действительно переданное сообщение. При малой помехе и, следовательно, малом отклонении Δs отрезок между s(t, b) и s(t, b̂) можно аппроксимировать прямой линией, которая является касательной к линии сигнала в точке s(t, b). Тогда Δs представляет проекцию n₁ вектора n на эту прямую. В этом случае справедливо представление^*

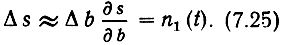
Здесь n₁(t) - составляющая шумового вектора в пространстве сигналов, представляющая низкочастотный гауссовский процесс со спектральной плотностью N₀ в полосе от 0 до F_c, Δb = b̂ - b. Тогда сообщение на выходе приемника

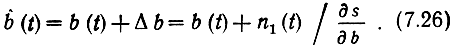
Чем больше производная ds/db, тем меньше шум, накладываемый на выходное сообщение, т. е. тем выше помехоустойчивость.

^* (При линейных методах модуляции представление (7.25), очевидно, справедливо для любой интенсивности помех.)

Отсюда следует что шум на выходе приемника

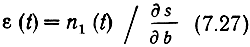
- есть гауссовский процесс с односторонней спектральной плотностью

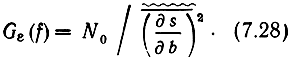
Здесь квадрат частной производной усредняется по времени и по ансамблю В (t).

Таким образом, при прямых системах модуляции шум на выходе приемника квазибелый, т. е. имеет равномерный спектр в полосе частот F_c.

В случае интегральных систем сообщение В (t) входит в выражения сигнала под знаком интеграла:

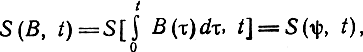
где

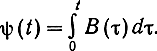
Так как B̂(t) = В (t) + ε(t), то

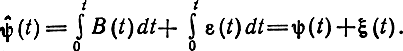
Следовательно, энергетический спектр шума на выходе приемника для таких систем можно определить как энергетический спектр производной ξ'(t). На основании известной теоремы о спектре производной G_ε(f) = (2πf)²G_ξ(f), где G_ξ (f) - определяется по формуле (7.28), если в последней вместо dS/dB подставить dS/dψ. Таким образом, для интегральных систем энергетический спектр шума на выходе приемника

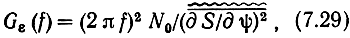
т. е. энергетический спектр помехи на выходе приемника в интегральных системах - параболический (пропорционален квадрату частоты). Все эти результаты получены для линейной модуляции или для слабых помех, когда можно считать

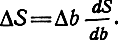
Они характеризуют так называемые нормальные ошибки (см. § 7.5).

Очевидно, мощность шума на выходе приемника в полосе частот от нуля до F_с

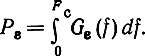
С другой стороны, мощность Р_B сообщения на выходе приемника, равную

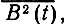
можно выразить через пик-фактор сообщения

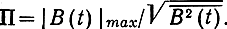
Учитывая принятое нормирование сообщения |В(i)| max = 1, получим

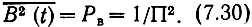
Тогда отношение мощностей сигнала и шума на выходе приемника

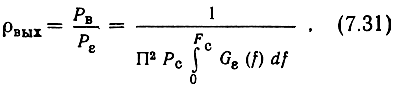
а выражения для выигрыша g и обобщенного выигрыша g' в соответствии с определениями (7.3) и (7.4) можно записать так:

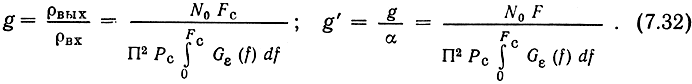
Для гармонического сигнала

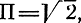
а для телефонного сообщения Π ≈ 3.

Используя теорему Шеннона (см. § 4.7), можно найти максимальные возможные значения выигрыша и обобщенного выигрыша при заданных параметрах системы связи. Рассмотрим этот вопрос для наиболее простого случая, когда непрерывное сообщение представляет гауссовский процесс с равномерным спектром в полосе частот F_с (квазибелый шум), а в канале существует аддитивная помеха в виде белого шума с односторонней спектральной плотностью NQ. Согласно теореме Шеннона передача сообщения с заданным значением Р_в/Р_ε = ρ₀ возможна в случае, когда Н'_ε(В) < С. Здесь Н'_ε(В) - эпсилон-производительность источника, которая в данном случае согласно (4.68) равна F_clog ρ₀, а С - пропускная способность гауссовского канала, равная согласно (4.48)

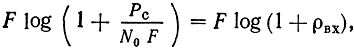
где F - полоса пропускания канала и в общем случае F ≠ F_c.

В гипотетической идеальной системе связи, в которой полностью используется пропускная способность канала и ρ_вых = ρ₀

В реальных системах связи обычно удается лишь частично использовать пропускную способность канала. Назовем эффективностью η системы связи отношение эпсилон-производительности источника к минимальной пропускной способности канала, при которой обеспечивается заданная верность, т. е. ρ_вых = ρ₀. Для такой реальной системы вместо (7.33) имеем

Из выражений (7.33) и (7.34) видно, что при ηF > F_c можно обеспечить высокую верность (большое значение ρ_вых) при относительно малых ρ_вх, т. е. получить большой выигрыш g.

Таким образом, выигрыш достигается в результате обмена ширины спектра на динамический диапазон, о чем говорилось в § 1.2. Большой выигрыш можно получить только при большом отношении α = F/F_c. Заметим, что большой выигрыш может иметь место и при малой эффективности η, и наоборот. Следовательно, при оценке различных систем связи необходимо учитывать, по крайней мере, два показателя: эффективность и помехоустойчивость. Совокупность этих двух показателей составляет достаточно полную характеристику системы.

Наилучшей считается система, которая обеспечивает наибольшую помехоустойчивость при заданной эффективности либо наибольшую эффективность при заданной помехоустойчивости.

Для идеальной системы η = 1 и из (7.33) следует

Отсюда при ρ_вх >> 1 получаем

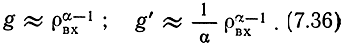
Таким образом, в идеальной системе выигрыш g возрастает с увеличением α по экспоненциальному закону. Никакая реальная система не может обеспечить при заданном α более высокую помехоустойчивость, чем идеальная.