7.2. Оптимальная оценка отдельных параметров сигнала

Задача оценки параметров сигнала возникает во многих практических случаях. Так, часто требуется определить (измерить) частоту или фазу сигнала, оценить изменение амплитуды при передаче сигнала по каналу. В телеметрии и телеуправлении необходимо оценивать большое число параметров, характеризующих состояние объекта. Таким объектом может быть технологический процесс, нефтепровод, летательный аппарат, экипаж и другие живые организмы, размещенные на летательных аппаратах и т. п. В этом случае передаваемыми сообщениями являются контролируемые параметры, представляющие собой случайные величины, не зависящие от времени. Модуляция при этом сводится к установлению некоторого параметра λ сигнала S (t) в соответствии с переданными сообщениями, а демодуляция - к выявлению (оценке) этого параметра с возможно большей точностью. Такая же задача возникает и при передаче сообщений, заданных на дискретных точках оси времени. В этом случае последовательно оценивают значения параметра (отсчета) на интервалах времени между дискретными точками.

В простейшем случае, когда оценивают один параметр сигнала заданной формы, задачу ставят следующим образом. Пусть принимаемое на интервале (0,T) колебание Z(t) представляет собой аддитивную смесь сигнала S(t,λ), зависящего от одного неизвестного параметра X, с белым шумом N(t):

Полагаем, что параметр λ имеет постоянное значение на интервале наблюдения (0, Т) и известна априорная плотность вероятности этого параметра w(λ). Требуется определить оператор системы, гарантирующий получение наилучшей оценки параметра и рассчитать точность этой оценки.

Из-за шума в канале и случайного характера параметра λ точное измерение его невозможно. Можно лишь указать приближенную его оценку. Очевидно, вся информация о переданном параметре (сообщении) λ после приема колебания Z(t) (7.5) содержится в апостериорном распределении w(λ|z), которое согласно формуле Байеса (6.5)

На основании анализа апостериорного распределения (7.6) принимается решение об оценке передаваемого параметра λ. При больших отношениях сигнал-шум апостериорная плотность вероятности имеет наибольший максимум в окрестности истинного значения параметра λ. Это обстоятельство указывает, что в качестве оценки целесообразно взять то значение λ, которое обращает в максимум функцию w(λ|z).

Во многих практических случаях априорная плотность вероятности w (λ) оказывается неизвестной и ее полагают равномерной w(λ) = const на некотором интервале Л. При этом координата максимума апостериорной вероятности будет совпадать с соответствующей координатой условного распределения w(z|λ), которое называют функцией правдоподобия. В этом случае правило максимума апостериорной вероятности переходит в правило максимального правдоподобия. Здесь оценка параметра λ определяется из условия

Оценку параметра, получаемую по этому критерию, называют максимально правдоподобной. Уравнение правдоподобия (7.7) можно записать в другом виде:

поскольку ln x - монотонная функция своего аргумента и, следовательно, корни (7.7) и (7.8) совпадают. Оценка определяется тем корнем уравнения (7.8), который соответствует максимуму функции правдоподобия. Другим, весьма распространенным критерием оценки параметров сигнала, является оценка по минимуму среднеквадратической ошибки. При этом критерии минимизируется по λ̂ выражение

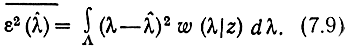
В этом случае оптимальная оценка λ̂ находится из условия

После дифференцирования выражения (7.9) по λ̂ с учетом, что ∫_A w (λ|z)dλ = 1, получаем

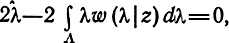
откуда

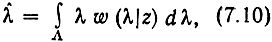
т. e. оптимальной оценкой параметра является математическое ожидание апостериорного распределения.

критерий среднеквадратической ошибки является частным случаев более общего критерия, когда минимизируется математическое (ожидание некоторой функции потерь L (λ-λ̇), т. е.

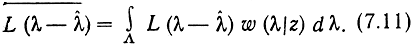
Оценку, минимизирующую эту величину, называют байесовской оценкой, а критерий (7.11), как и в дискретном случае [см.(6.13) ], - критерием среднего риска. При L(λ-λ̇) = (λ-λ̇)² критерий минимума среднего риска (7.11) переходит в критерий среднеквадратической ошибки (7.9). В этом случае байесовская оценка определяется выражением (7.10).

Если w(λ|z) симметрична относительно λ̇_oпт, что имеет место при большом отношении сигнал-шум, то критерии максимума апостериорной вероятности или максимума функция правдоподобия совпадают с критерием минимума среднеквадратической ошибки.

Если значение параметра λ, постоянно на интервале наблюдения и принятое колебание представляет собой аддитивную смесь (7.5) полезного сигнала S(t, λ) и нормального белого шума N (t) со спектральной плотностью N₀/2, то вектор Z, определяющий принимаемое колебание в функциональном пространстве, является случайным гауссовским вектором, среднее значение которого s(t, λ), а дисперсия совпадает с дисперсией шума.

Рассуждая так же, как в § 6.3, на основании (6.19)

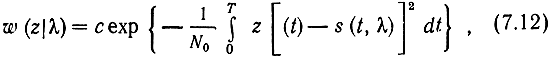
где с - постоянный коэффициент, а согласно (7.6) и

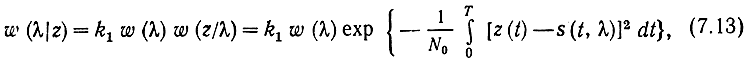
где k₁ - некоторая постоянная, которая может быть вычислена из условия нормирования ∫_λ w(λ|z)dλ = 1. Упростим это выражение, преобразовав показатель экспоненты

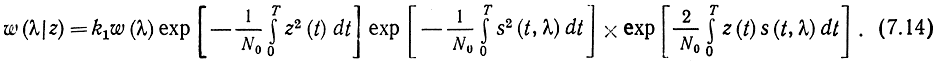
В правой части этого равенства первый экспоненциальный множитель не зависит от λ и его можно включить в постоянную k₁. Второй множитель равен ехр (-E/N₀), где Е - энергия сигнала. В тех случаях, когда параметр λ не энергетический, т. е. энергия сигнала не зависит от λ, этот член также можно включить в постоянную k₁. При этом условии выражение (7.14) можно записать так:

где

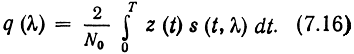
Нетрудно убедиться, что для сигнала S(t), зависящего от нескольких параметров, функция правдоподобия до w/(z|λ) и апостериорная плотность вероятности w(λ|z) будет определяться аналогичными выражениями, в которых λ = (λ₁, λ₂,..., λ_n).

Отсюда следует, что при известной априорной вероятности определение апостериорной вероятности сводится к вычислению функция q(λ). Эта функция, с точностью до коэффициента, (равна скалярному произведению пришедшего сигнала на ожидаемый вариант сигнала s(t, λ). Ее часто называют корреляционным интегралом. Она определяет те существенные операции, которые нужно выполнить над z(t), чтобы извлечь всю доступную информацию о переданном сообщении λ. Оптимальный приемник максимального правдоподобия воспроизводит то сообщение λ, для которого функция q(λ) максимальна.