Глава 10. Методы повышения эффективности систем передачи информации

10.1. Предельная эффективность СПИ

Системы связи для передачи дискретных и непрерывных сообщений, несмотря на их различие как по назначению, так и по способам реализации, характеризуются качественными показателями, которые были перечислены в § 1.7. Основные из них - скорость и верность передачи.

Для обеспечения необходимой скорости передачи информации при заданной верности приходится затрачивать некоторую мощность сигнала и занимать определенную полосу частот в канале связи. Какие мощность и полоса частот при этом потребуются, зависит от применяемой системы связи. Представляет интерес сравнить между собой различные системы связи по степени использования ими основных ресурсов канала - пропускной способности, мощности сигнала и занимаемой полосы частот. Ниже это сравнение проводится для некоторых систем в случае, когда сигналы передаются в канале с аддитивным гауссовским белым шумом. Верность передачи будем считать заданной; она характеризуется при передаче дискретных сообщений вероятностью ошибки, а при передаче непрерывных сообщений - отношением сигнал- шум на выходе демодулятора.

Для оценки эффективности систем связи введем коэффициент использования канала по мощности β (энергетическую эффективность) и коэффициент использования канала по полосе частот у (частотную эффективность):

где R - скорость передачи информации; ρ₀ - отношение мощности сигнала Р_с к спектральной плотности N₀ мощности шума; F - ширина полосы частот, занимаемой сигналом.

Как видно, безразмерные коэффициенты β и γ имеют смысл удельных скоростей (скоростей отнесенных к одному из параметров канала). Так, коэффициент γ определяет скорость передачи информации в единичной полосе частот.

Обобщенной характеристикой эффективности систем связи является коэффициент использования канала по пропускной способности (информационная эффективность)

С учетом формулы Шеннона

где ρ = Р_с/Р_ш - отношение мощностей сигнала и шума в полосе F, получаем следующие выражения:

Согласно теореме Шеннона при соответствующих способах передачи (кодирования и модуляции) и приема (демодуляции и декодирования), величина т) может быть сколь угодно близка к единице при сколь угодно малой вероятности ошибок. В этом случае из условия η = 1 получаем предельную зависимость между р и у:

Эту зависимость удобно представить в виде кривой на плоскости βγ (рис. 10.1). Полученная кривая является предельной и отражает наилучший обмен между β и γ в непрерывном канале (НК). Следует заметить, что частотная эффективность γ изменяется в пределах от 0 до ∞, в то время как энергетическая эффективность ограничена сверху

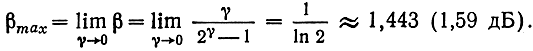
Аналогичные предельные кривые можно построить и для любых других каналов, если в (10.1) и (10.2) вместо скорости R подставить выражение для пропускной способности соответствующего канала.

На рис. 10.1 приведены кривые для симметричных дискретных (ДСК) и полунепрерывных (ПНК) каналов при основании кода сигнала М = 2 и 4. Ограничение объема алфавита канальных символов (сигналов), как видно, прежде всего ведет к ограничению частотной эффективности

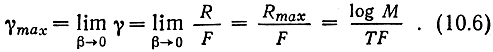
Отсюда для двоичного канала (М = 2) с противоположными сигналами при 2TF = 1 γ_max = = 2 бит/сГц (предел Найквиста) и β_max = -0,4 дБ. В полунепрерывном канале при γ→0 кривая энергетической эффективности β асимптотически приближается к предельной кривой для непрерывного канала. При логарифмическом масштабе в соответствии с соотношением γ = ρβ линии одинаковых значений превышения сигналов над шумом представляют собой прямые с углом наклона 45°.

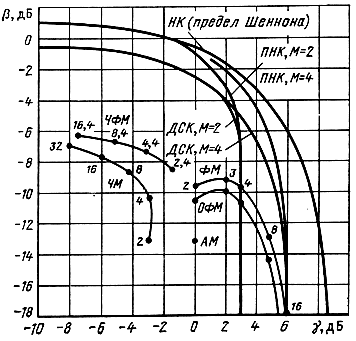
Рис. 10.1. Кривые предельной энергетической и частотной эффективности систем передачи информации

В реальных системах вероятность ошибки р всегда имеет конечное значение и η<1. В этих случаях при p = const можно определить отдельно р и γ и построить кривые β = f(γ). В координатах р и γ каждому варианту реальной системы будет соответствовать точка на плоскости. Все эти точки (кривые) располагаются ниже предельной кривой Шеннона. Ход этих кривых зависит от вида сигналов (модуляции), кода и способа обработки сигналов.

Цифры на кривых рис. 10.1 указывают число позиций сигнала М. Кривые рассчитаны на основании формул гл. 6 для оптимального приема сигналов при равной априорной вероятности их передачи и вероятности ошибки p = 10^-5. При этом принималось R≈v = 1/T и h² = E/N₀ = 1/Р; F=M/T log M для ЧМ и F = 1/T log M для ФМ [5]. Здесь Т - время, затрачиваемое на передачу 1 бита.

Из рис. 10.1 видно, что в системах с ЧМ при увеличении числа позиций М энергетическая эффективность р увеличивается, а частотная эффективность γ - уменьшается. В системах с ФМ и ОФМ наоборот, с увеличением М коэффициент β уменьшается, а γ - увеличивается.

Таким образом условия обмена β на γ за счет изменения числа сигналов с ЧМ и ФМ различные. Причины этого обсуждались в конце гл. 9. При частотно-фазовой модуляции (ЧФМ) достигается некоторый компромисс в получении необходимых значений γ и β. Элементарным сигналом при ЧФМ является колебание с одной из n частот, фаза которого принимает одно из m фиксированных значений. Общее число сигналов в ансамбле М = nm. На кривой для ЧФМ первая цифра указывает число частотных позиций, а вторая - число позиций фазы.

Полученные таким образом βγ-диаграммы позволяют сравнительно быстро определить системы, удовлетворяющие заданным требованиям по энергетической и частотной эффективности и установить, насколько эти показатели для реальных систем близки к предельным. Анализ предельных кривых показывает, что эффективность систем связи можно существенно повысить, если перейти от дискретных каналов к каналам с непрерывным выходом (полунепрерывные каналы) и многопозиционными сигналами (М>2).

Совокупность кривых β = f(γ) позволяет выбрать наилучшую систему при заданных ограничениях на верность передачи. После того как выбрана система по показателям β и γ, по формуле (10.4) можно вычислить обобщенный показатель технического эффекта η - информационную эффективность. Так, по данным рис. 10.1 имеем: η≈0,23 для АМ₂; 0,15 для ЧМ₂; 0,25 для ФМ₂; и 0,47 для ФМ₄.

Однако при создании новых систем или при сравнении существующих систем оценки эффективности по техническим (информационным) показателям совершенно недостаточно. Любая техническая задача всегда решается так, чтобы построить наиболее экономичную систему, характеристики которой удовлетворяют заданном требованиям. Необходим технико-экономический подход, при котором совместно учитываются экономические и технические показатели. Одним из таких подходов является принцип минимальных затрат, согласно которому лучшей считается та система, для реализации и эксплуатации которой требуются наименьшие затраты при заданном техническом эффекте. В качестве технического эффекта можно принять информационную эффективность η при допустимой верности передачи. Таким образом, выбор систем по показателям β и γ является исходным для последующего технико-экономического анализа систем.