10.3. Многопозиционные сигналы и корректирующие коды

Ансамбль сигналов {s_i(t)}^M_i=1 на интервале (0, Т) можно представить в виде

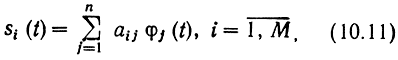
где {φ_j(t)} - система базисных ортонормальных функций:

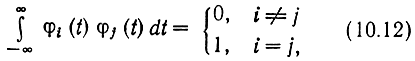
(см. § 2.5);

n - число измерений (отсчетов) на интервале Т (для финитных сигналов, энергия которых почти полностью сосредоточена в полосе F, n = 2TF). Коэффициенты разложения в (10.11).

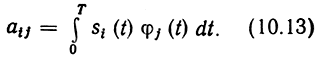
Геометрически каждому сигналу ансамбля соответствует точка (или ректор) в n-мерном пространстве с координатами (a_i1, a_i2,....,a_in i = 1,...., М. Энергия сигнала при этом равна квадрату

его нормы:

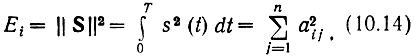
а расстояние между сигналами

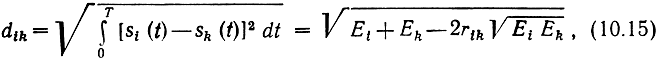
где

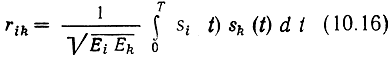
- коэффициент взаимной корреляции рассматриваемых сигналов. В дальнейшем будем рассматривать ансамбли сигналов с одинаковыми энергиями E_i = E_k = E.

Примером одномерных сигналов (n = 1) являются двоичные противоположные сигналы, которым соответствует две симметрично расположенные точки на прямой с координатами (0, √E и (0, -√E). Расстояние между сигналами d₁₂ = 2√E, а коэффициент корреляции r₁₂ = - 1. Двоичные ортогональные сигналы являются примером двумерных сигналов (n = 2). Им соответствует два ортогональных вектора на плоскости с координатами (√E, 0) и (0, √E). Расстояние между сигналами d₁₂ = √2E, а коэффициент корреляции r ₁₂ = 0.

Наиболее распространенными многопозиционными сигналами являются ортогональные, биортогональные и симплексные. Если сигнальные точки выбрать на линиях, совпадающих с ортами φ на расстояниях √E от начала координат, то получим систему ортогональных сигналов. Число сигналов в таком ансамбле М = n. Так, если принять

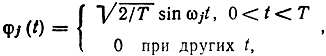
то согласно (10.11)

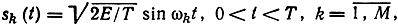
т. e. сигналы являются отрезками гармонических колебаний разных частот ω₁, ω₂, ..., ω_M, удовлетворяющих условию ортогональности. Это известные сигналы многочастотной модуляции (МЧМ).

Ортогональные сигналы образуют эквидистантную систему, расстояния между любыми двумя сигнальными точками которой одинаковы и, согласно выражению (10.15), равны d = √2E. Биортогональные сигналы образуются по следующему правилу: к каждому ортогональному сигналу добавляется противоположный. Здесь число сигналов М = 2n. Простейшим из биортогональных

является ансамбль с М = 4. Сигналы имеют одинаковые энергии и находятся на одинаковом расстоянии от начала координат. На (плоскости они образуют квадрат (рис. 10.4). При выборе в качестве базисных функций

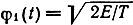
и

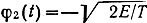
сигналы ансамбля

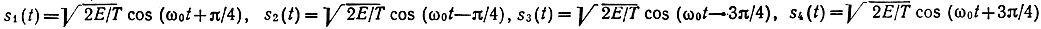
отличаются только начальными фазами. Это широко используемые сигналы с фазовой модуляцией и числом позиций М = 4 (ФМ₄). Расстояние между ближайшими сигналами этого ансамбля √2E а между противоположными сигналами - 2√E.

Известные сигналы с амплитудно-фазовой модуляцией (АФМ) образуют круговую сеть (см. рис. 10.4): например, три сигнала равномерно распределены по окружности, а четвертый расположен в центре окружности. В том же базисе они могут быть представлены так:

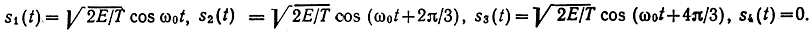
Симплексные сигналы отстоят друг от друга на одинаковом расстоянии. В n-мерном пространстве они образуют правильный симплекс с числом вершин М= n + 1. В двумерном пространстве это равносторонний треугольник (см. рис. 10.4), а в трехмерном - тетраэдр. Расстояние между сигнальными точками симплексного ансамбля равно

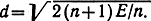
При n - 1 симплексные сигналы совпадают с противоположными.

Многопоэиционные сигналы с фазовой модуляцией (ФМ) образуют круговую сеть с равномерным распределением точек по окружности. Построить ансамбли ортогональных и биортогональных многопозиционных сигналов можно и на основе двоичных последовательностей. Для этого обычно используют элементарную матрицу Адамара А, повторением которой трижды в позитивной и один раз в негативной форме можно увеличить размеры матрицы каждый раз вдвое и получить матрицу Б, которая представляет ансамбль ортогональных сигналов с М = 4:

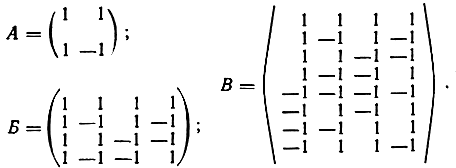
Каждая строка этой матрицы (последовательность двоичных символов) образует один сигнал. Нетрудно проверить, что эти строки (сигналы) взаимноортогональны. Дополняя матрицу Б инверсиями строк, получим матрицу В, представляющую ансамбль М = 8 биортогональных сигналов. Аналогично строятся ансамбли с большим числом сигналов М. Симплексные сигналы также могут быть получены на основе двоичных последовательностей [12].

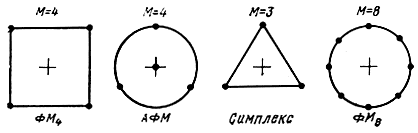
Рис. 10.4. Примеры ансамблей двумерных сигналов

Помехоустойчивость систем связи в общем случае зависит как от вида передаваемых сигналов, так и от способа приема. При оптимальном приеме реализуется потенциальная помехоустойчивость. Алгоритм оптимального приема М-позиционных сигналов определяется системой неравенств (6.23), а вероятность ошибки вычисляется как вероятность невыполнения этих неравенств.

В § 6.5 получены выражения для вероятности ошибки при М = 2. Для не двоичных систем (М>2) получить такие простые выражения не всегда удается. Для некоторых ансамблей сигналов такие формулы имеются в [8], а для других, путем численного интегрирования, получены графики зависимости p = f(E/N₀) [12, 18], которые ниже используются для вычисления энергетической эффективности р. Для приближенных вычислений при симметричных системах можно воспользоваться верхней оценкой (6.60)

где P₂(s_i, s_j)-вероятность ошибки в системе, использующей сигналы s_i и s_j для передачи двух равновероятных сообщений.

При одном и том же способе приема различные ансамбли сигналов будут обеспечивать разную помехоустойчивость. Объясняется это особенностями расположения границ областей правильного приема, окружающих каждый сигнал [(см. рис. 6.1). Минимум средней вероятности ошибки достигается при размещении границ на равных расстояниях от соседних сигнальных точек. Поиск наилучшего ансамбля сводится к нахождению такого расположения сигнальных точек, при котором области сигналов имеют наибольшую величину, наиболее близки одна к другой по размерам и приближаются по форме к окружностям. Это известная в многомерной геометрии задача плотнейшей укладки одинаковых шаров в заданном объеме. Такое расположение обеспечивает одинаковую вероятность ошибок для любого сигнала (области сигналов одинаковы) и минимальную среднюю энергию сигналов (области наиболее плотно упакованы).

На рис. 10.5 приведены βγ-диаграммы для некоторых ансамблей двумерных многопозиционных сигналов. Значения энергетической эффективности определялись по кривым помехоустойчивости p = f(E/N₀) [12] для заданного значения вероятности ошибки на бит р= 10~5, поскольку при малой вероятности ошибки (р>10^-3) R≈1/T и β =1/(E/N₀), а частотная эффективность согласно (10.6)

Различают два класса многопозиционных сигналов. Первый образуют "плотные" сигналы, когда с ростом объема ансамбля М при фиксированной размерности n расстояние между сигналами уменьшается, а удельная скорость γ, согласно (10.18) возрастает при соответствующем снижении энергетической эффективности β. В качестве примера таких сигналов на рис. 10.5 приведены кривые для многопозиционных сигналов ФМ и АФМ.

Биортогональные, симплексные и ортогональные сигналы являются примером другого класса "разнесенных" сигналов, когда с увеличением М расстояние между сигналами увеличивается и соответственно увеличивается энергетическая эффективность за счет снижения частотной эффективности γ. Центральное место на диаграмме рис. 10.5 занимает система с сигналами ФМ4, которые относятся к классу биортогональных при М = 4. Из простых систем- это наиболее эффективная система (γ = 2, β = -9,6 дБ, η = 0,47). В спутниковых сетях ФМ₄ является наиболее распространенной и принята в качестве стандарта. Поэтому при сравнительной оценке эффективности систем целесообразно принять за эталон систему с ФМ₄. Если начало координат перенести в точку, соответствующую ФМ₄, то в новой системе координат по вертикальной оси будет отсчитываться энергетический выигрыш Δβ рассматриваемых систем по сравнению с ФМ₄, а по горизонтальной оси - выигрыш Δγ по удельной скорости. В этой системе координат все возможные СПИ можно условно разделить на четыре группы, соответствующие четырем квадрантам на плоскости: 1-малоэффективные системы (III квадрант), имеющие относительно ФМ₄ проигрыш по β и γ (например, АМ₂, ЧМ₂); 2 - системы с высокой энергетической эффективностью (II квадрант), обеспечивающие выигрыш по β и проигрыш по γ (системы с корректирующими кодами); 3 - системы с высокой частотной эффективностью (IV квадрант), обеспечивающие выигрыш по γ и проигрыш по β (системы с многопозиционными ФМ и АФМ сигналами) и 4 - высокоэффективные системы (I квадрант), позволяющие получить одновременно выигрыш по обоим показателям β и γ (сложные сигнально-кодовые конструкции).

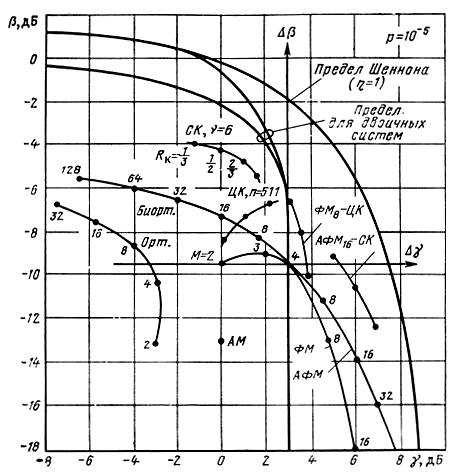
Рис. 10.5. Кривые энергетической и частотной эффективности систем с многопозиционными сигналами и корректирующими кодами

Приведенные на рис. 10.5 βγ-диаграммы позволяют количественно оценить обменный выигрыш (проигрыш) различных систем. Так, например, применение биортогональных сигналов с М = 16 позволяет получить энергетический выигрыш Др = 2,4 дБ в обмен на снижение удельной скорости γ в 2 раза (3 дБ). Обмен энергетической эффективности на частотную можно осуществить с помощью многопозиционных сигналов с ФМ. Однако более эффективными являются АФМ сигналы.

Наряду с многопозиционными сигналами для повышения эффективности СПИ широко используются помехоустойчивые коды. Применение корректирующих кодов позволяет повысить верность передачи сообщений или при заданной верности повысить энергетическую эффективность системы. Последнее особенно важно для систем с малой энергетикой (систем спутниковой и космической связи). На практике используются как блочные, так и непрерывные коды. На рис. 10.5 приведены кривые эффективности для циклического кода (ЦК) и для сверточного кода (СК) с декодированием по алгоритму Витерби. Здесь n - длина кодовой последовательности, v - кодовое ограничение, R_K - скорость кода. Как видим, применение циклического кода позволяет получить энергетический выигрыш Δβ = 2 - 3 дБ, а сверточный код - Δβ = 5-6 дБ в обмен на снижение частотной эффективности в 2 раза (3 дБ). Применение каскадных кодов, как показывают расчеты, позволяет получить еще больший энергетический выигрыш и существенно приблизиться к предельной кривой для двоичных систем. Энергетический выигрыш Δβ от применения помехоустойчивого кодирования тем больше, чем выше требуемая верность передачи. Для непрерывного постоянного канала с белым шумом при требуемой вероятности ошибки 10^-5 предельный энергетический выигрыш кодирования Др по сравнению с ФМ₂ без кодирования и оптимальном когерентном приеме составляет примерно 10 дБ. При современной элементной базе затраты на реализацию кодирующих и декодирующих устройств значительно сократились, в то время как стоимость энергетики канала практически не изменилась. Таким образом "цена" выигрыша Δβ за счет кодирования может быть существенно меньше цены того же выигрыша, полученного за счет увеличения энергетики канала (мощности сигнала или размеров антенн).

Расчетные кривые на рис. 10.5 показывают, что применение циклического кода в канале с ФМ или сверточного кода в канале с АФМ позволяет получить одновременно выигрыш как по энергетической, так и по частотной эффективности или во всяком случае выигрыш по одному показателю без ухудшения другого. Построение таких высокоэффективных систем (η>0,5) на основе сложных сигнально-кодовых конструкций ведет к неизбежному увеличению сложности системы. Не пропускная способность (предел Шеннона), а сложность является ограничивающим фактором при построении высокоэффективных систем. Задача состоит в том, чтобы построить систему удовлетворяющую высоким показателям эффективности, при минимальной (допустимой) сложности, а следовательно, и стоимости системы.