§ 1.13. Комплексные числа

Комплексным числом называют сумму действительного и мнимого чисел, например a + jb, где a и b - действительные числа; 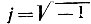- мнимая единица.

Число а + j0 = а является действительным числом, а число 0 + jb = jb - мнимым. Мнимая единица обладает таким свойством, что jj = j² = - 1; j³ = - j и т. д.

Два комплексных числа a + jb и c + jd равны, если равны их действительные и мнимые части: а = с; b = d. Два комплексных числа a + jb и a - jb называют сопряженными. Комплексное число можно представить вектором на комплексной плоскости, проведенным из начала координат 0 в точку K (рис. 1.3).

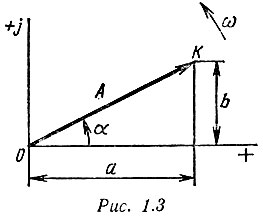
Рис. 1.3

Длину вектора, изображающего комплексное число, называют модулем этого числа 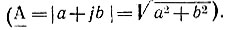Аргументом комплексного числа аα является угол между осью действительных значений и вектором, изображающим комплексное число аα = arctg b/a.

Умножение комплексного числа на ±j означает поворот вектора против (по) часовой стрелки на 90° без изменения его длины.

Комплексную величину, изображающую гармоническую функцию времени, отмечают точкой наверху 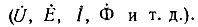Другие комплексные величины подчеркивают снизу 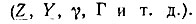Вещественная и мнимая части комплексной величины обозначаются следующим образом:

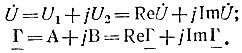
Существует несколько форм записи комплексного числа.

Комплексные числа