§ 1.14. Основные комплексные величины и законы, характеризующие гармоническое напряжение (ток)

Гармонические функции изображают графически синусоидами (косинусоидами), или векторами на комплексной плоскости (рис. 1.4).

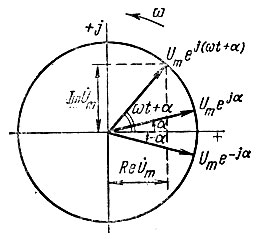
Рис. 1.4

Мгновенное значение гармонической функции представляет проекцию вращающегося вектора на неподвижную ось. Синусоидально изменяющаяся функция изображается проекцией на мнимую ось:

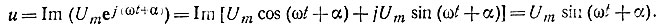
Косинусоидально изменяющаяся функция изображается проекцией на вещественную ось:

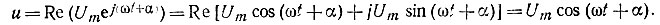
За положительное направление вращения комплексного вектора с угловой частотой ω принимают направление вращения против часовой стрелки. Поэтому положительную фазу α откладывают от полуоси вещественных значений против, а отрицательную фазу - α - по часовой стрелке. Взаимное расположение векторов на комплексной плоскости с течением времени не изменяется, поэтому их расположение рассматривают только в начальный момент времени ωt = 0. Векторы, изображающие на комплексной плоскости напряжения и токи в рассчитываемой схеме, образуют векторную диаграмму (рис. 1.5). Операции сложения, вычитания, умножения и деления гармонических функций производят путем сложения, вычитания; умножения и деления векторов на комплексной плоскости. Обычно на комплексной плоскости откладывают комплексы действующих значений.

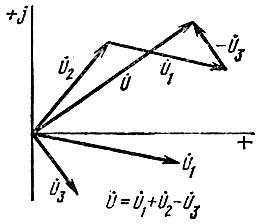
Рис. 1.5

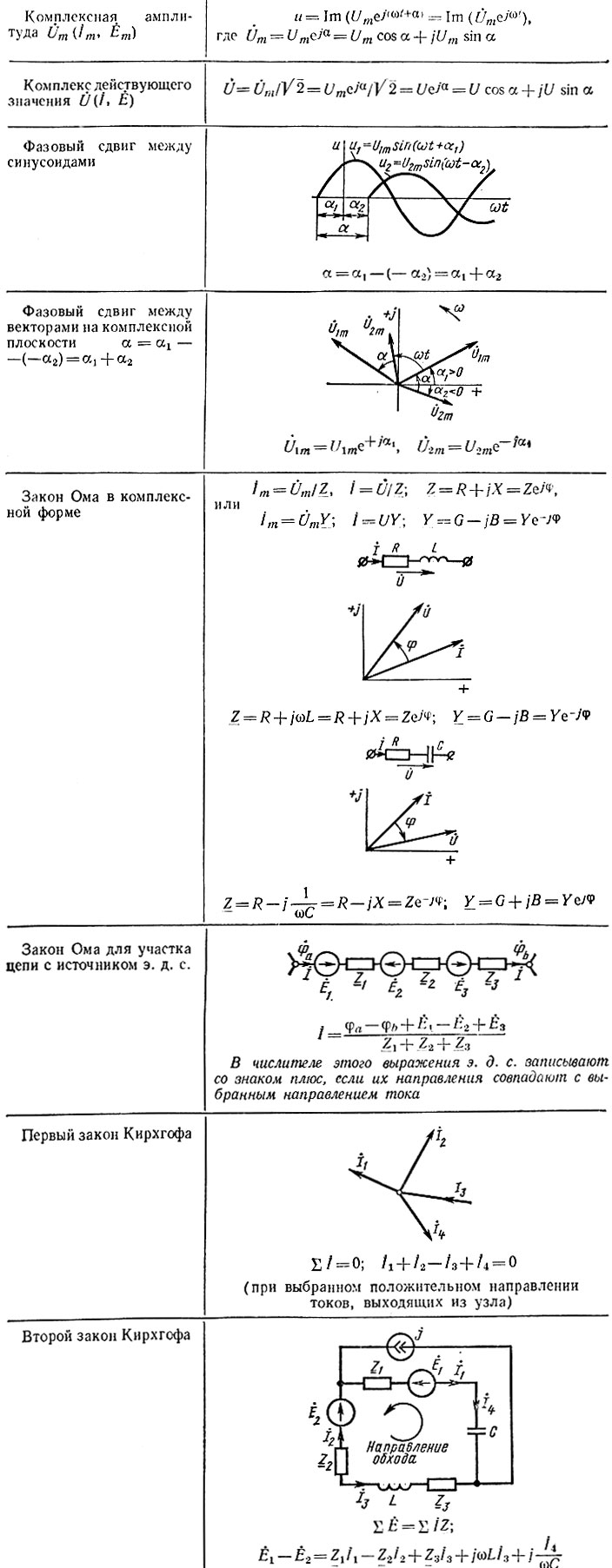
Основные комплексные величины и законы, характеризующие гармоническое напряжение (ток)