§ 1.24. Круговая диаграмма для токов четырехполюсника

Входной ток четырехполюсника I^·₁ (рис. 1.8) изменяется в соответствии с уравнением окружности, центр которой в общем случае не лежит в начале координат:

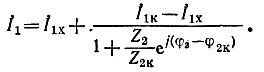
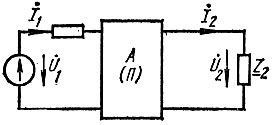
Рис. 1.8

Геометрическое место конца вектора тока 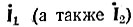является окружностью при постоянных входном напряжении 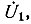частоте ω, аргументе φ₂ и изменяющемся по величине сопротивлении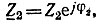

Последовательность построения диаграммы (рис. 1.9):

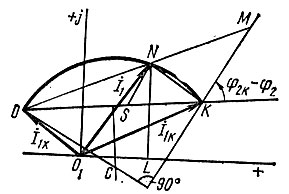
Рис. 1.9

1. Входные токи I^·_1к и I^·_1х определяют соответственно при закороченных (Z₂ = 0) и разомкнутых (Z₂ = ∞) вторичных зажимах четырехполюсника.

2. Вычисляют аргумент φ_2к входного сопротивления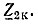

3. На комплексной плоскости в произвольном масштабе строят векторы I^·_1к и I^·_1x. Разность I^·_1к - I^·_1x является хордой искомой окружности (ОК).

4. Под углом φ_2к - φ₂ к хорде в конце вектора I^·_1к проводят прямую линию, на продолжении которой спускают перпендикуляр из конца вектора I^·_1x. Если угол (φ_2к - φ₂) > 0, то его откладывают против часовой стрелки и наоборот. К середине хорды восстанавливают перпендикуляр. Центр окружности лежит в точке пересечения этих двух перпендикуляров (точка С).

5. Рабочая часть хорды расположена по ту же сторону от хорды, что и угол φ_2к - φ₂.

6. Параметры схемы определяют с помощью круговой диаграммы.

Круговая диаграмма для токов четырехполюсника