Глава 5. Топологические методы расчета электрических схем

§ 5.1. Основные понятия и определения

Топологические методы расчета электрических схем основаны либо на аналитическом, либо на геометрическом способе описания свойств графа, изображающего исследуемую электрическую цепь.

Аналитическое описание свойств графа, введенное еще Кирхгофом, основывается на применении матричной алгебры.

При геометрическом описании используют правила по преобразованию графов и правило Мэзона (Масона).

Матричная теория графов позволяет записать выражения для определителя и алгебраических дополнений без составления уравнений электрической схемы, что значительно сокращает вычисления при разложении определителей обычным алгебраическим способом. Это объясняется тем, что при раскрытии определителей, и алгебраических дополнений появляются слагаемые, имеющие одинаковые величины с противоположными знаками, которые затем сокращаются.

Схема электрической цепи - графическое изображение электрической цепи, содержащее условные обозначения ее элементов, показывающее соединения этих элементов. Нумеруются узлы, ветви и задаются направления токов (рис. 5.1).

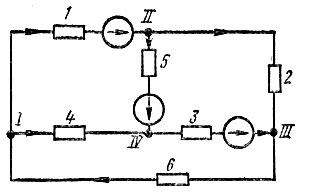
Рис. 5.1

Граф электрической схемы - условное изображение схемы электрической цепи, в котором ветви схемы представлены отрезками - ветвями графа, а узлы точками - узлами графа. Узлы и ветви графа соответствуют узлам и ветвям электрической схемы (рис. 5.2). Подграф схемы - часть графа схемы.

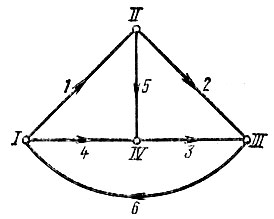
Рис. 5.2

Направленный граф схемы - граф с указанием условно-положительных направлений токов или напряжений в виде отрезков со стрелками.

При составлении графа ветви, содержащие только идеальные источники напряжения (идеальные источники тока), необходимо преобразовать (см. § 1.3). Преобразование ветви с идеальным источником э. д. с. приводит к ее закорачиванию и переносу э. д. с. в ветви, присоединенные к этому узлу. Преобразование ветви с идеальным источником тока приводит к ее размыканию и подключению таких же источников тока параллельно ветвям, присоединенным к этим узлам.

Дерево графа схемы - любая совокупность ветвей графа, соединяющих все его узлы без образования контуров. Заданный граф имеет несколько деревьев. Число возможных деревьев n_д равно определителю ΔУ, составленному по методу узловых потенциалов, если считать, что проводимость каждой ветви схемы равна единице, Число возможных деревьев графа рис. 5.2 n_д = 16 (рис. 5.3).

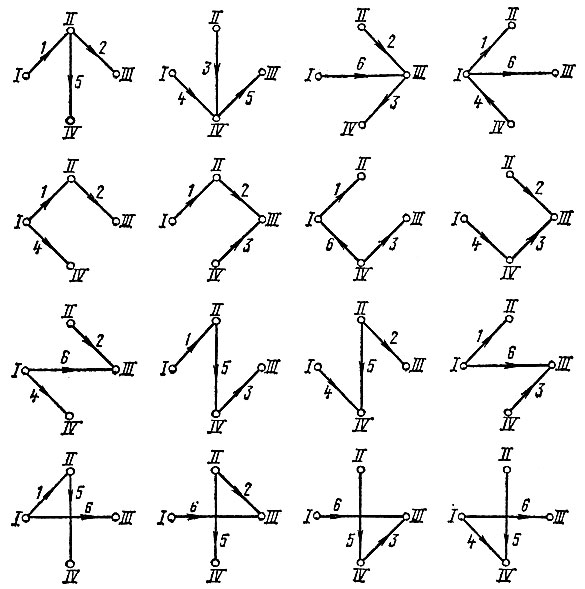
Рис. 5.3

Величина дерева - произведение проводимостей всех ветвей дерева.

Сумма величин всех деревьев равна определителю матрицы узловых напряжений.

Ветвь связи (главная ветвь) - ветвь графа, не принадлежащая дереву.

Величина связи - произведение сопротивлений всех ветвей связи. Сумма величин всех связей равна определителю матрицы контурных токов.

Главный контур (независимый контур) - образован ветвями дерева и одной ветвью связи.

Путь графа - непрерывная последовательность ветвей, проходящих не более одного раза через каждый узел. Для графа (рис. 5.4) между узлами II и III путь образован следующими ветвями: 2, 5-3, 1-4-3, 1-6.

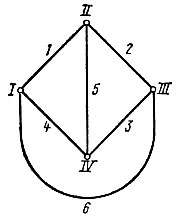
Рис. 5.4

Сечение графа - совокупность ветвей, рассечение которых делит граф на два изолированных подграфа. Ветви 1-4-6, 1-5-2 образуют сечение (рис. 5.5). Сечением может быть изолированный узел.

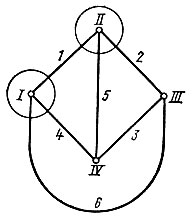
Рис. 5.5

Главное сечение графа содержит ветви связи и только одну ветвь дерева. Номер сечения соответствует номеру ветви дерева, пересекаемой сечением. За положительное направление сечения обычно принимают направление ветви дерева (рис. 5.6).

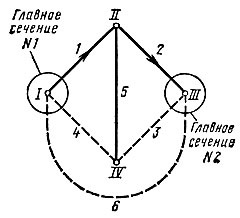
Рис. 5.6