§ 5.2. Топологические матрицы графа

Геометрия каждого графа может быть описана несколькими матрицами (таблицами чисел). В литературе нет единого названия и обозначения каждой матрицы. При расчете используют матрицу соединений, контурную матрицу, матрицу главных сечений, матрицы параметров ветвей и др.

Матрица соединений. Данная матрица (структурная или узловая матрица) определяет схему электрической цепи и является таблицей коэффициентов уравнений, составленных по первому закону Кирхгофа. Строки матрицы соответствуют узлам, а столбцы - ветвям направленного графа схемы. Различают полную матрицу соединений Α_п и просто матрицу соединений Α. В полной матрице соединений число строк соответствует числу всех узлов графа, а в матрице соединений - числу независимых узлов. Матрица Α может быть получена, если в матрице Α_п вычеркнуть одну из строк. Узел, соответствующий вычеркнутой строке, называют базисным. Таким образом, матрицу соединений Α составляют для независимых узлов графа, она содержит в качестве элементов +1, -1 и 0.

Если ветвь m направлена от узла n, то в клетку пересечения m-го столбца и n-й строки записывают +1; если ветвь m направлена к узлу n, то в соответствующей клетке записывают -1. Если ветвь m не соединена с узлом n, то в клетке пересечения ставят 0.

Матрица соединений для графа с базисным узлом IV (см. рис. 5.2) представлена табл. 5.1.

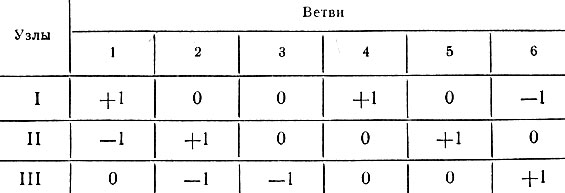
Таблица 5.1

Контурная матрица Β. При составлении контурной матрицы выбирают направление обхода независимых контуров графа. Число строк контурной матрицы равно числу независимых контуров, а число столбцов - числу ветвей графа, Если направление обхода контура k совпадает с направлением ветви l, входящей в этот контур, то в клетку пересечения k-й строки и l-го столбца записывают +1, если направление ветви противоположно направлению обхода контура, то в соответствующую клетку вписывают -1. Если же ветвь l не входит в контур k, то в эту клетку ставят 0. Для графа рис. 5.2 контурная матрица составления при обходе контуров по часовой стрелке дана табл. 5.2.

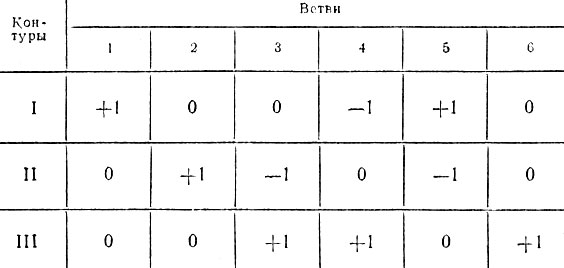
Таблица 5.2

Матрица главных сечений Q. Данную матрицу можно представить в виде таблицы коэффициентов уравнений, составленных по первому уравнению Кирхгофа для главных сечений. Строки матрицы соответствуют сечениям, столбцы - ветвям. В клетке пересечения i-й строки и j-го столбца записывают +1, если j-я ветвь имеет то же направление по отношению к сечению, что и ветвь дерева. В противном случае в эту клетку ставят -1. Если ветвь не входит в сечение i, то в соответствующую клетку вписывают 0.

Для графа рис. 5.7 и выбранного дерева с ветвями 1-5-2 матрица главного сечения представлена табл. 5.3.

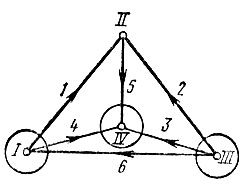
Рис. 5.7

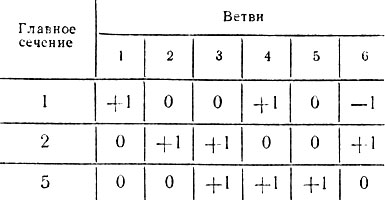
Таблица 5.3

К матрицам параметров ветвей относят матрицы сопротивлений и проводимостей ветвей, а также столбцовые матрицы источников э. д. с. и токов, матрицу токов ветвей.

Матрица сопротивлений ветвей Ζ_в. В этой матрице номера строк и столбцов соответствуют номерам ветвей. На пересечении m-й строки и n-го столбца записывают сопротивления взаимной связи m-й и n-й ветвей. Матрица сопротивлений всегда квадратная, по ее диагонали записывают собственные сопротивления ветвей.

Если взаимные связи отсутствуют, то матрица диагональная. Для цепи с четырьмя ветвями без взаимных связей матрица сопротивлений

Чтобы получить более упорядоченную матрицу, целесообразно сначала нумеровать все индуктивные элементы, затем емкостные и наконец резистивные элементы. Число ветвей (порядок матрицы) равно числу элементов.

В табл. 5.4 записана матрица сопротивлений для схемы рис. 5.8.

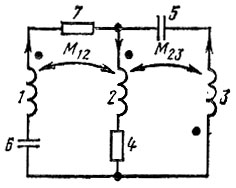
Рис. 5.8

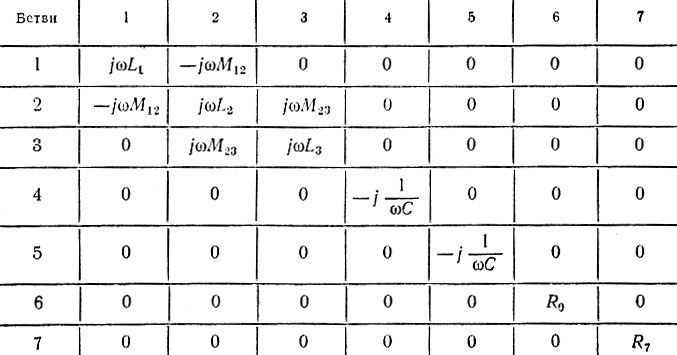
Таблица 5.4

Для уменьшения порядка матрицу Ζ_в целесообразно разбить на подматрицы, каждую из которых можно обозначить соответственно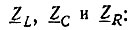

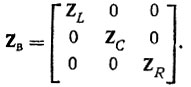
Матрица проводимостей ветвей Υ_в. Эта матрица, обратная матрице сопротивлений Ζ_в:Υ_в = Ζ_в^-1. При индуктивных связях элементы матрицы Υ_в не равны проводимостям ветвей. Данная матрица симметрична относительно диагонали, если соблюдается свойство взаимности.

Матрица э. д. с. источников Е. Это столбцовая матрица, число строк которой равно числу ветвей графа. э. д. с. E записывают с положительным знаком в соответствующей строке, если ее направление совпадает с выбранным направлением ветви:

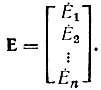
Матрица источников тока J. Эта матрица является столбцовой, число строк которой равно числу ветвей графа. Ток источника в матрице имеет знак плюс, если при обходе контура, образованного источником тока и параллельной ему ветвью, в направлении ветви заданное направление источника тока совпадает с направлением обхода:

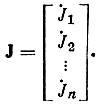
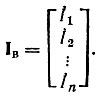
Матрица токов ветвей Ι_в. Это столбцовая матрица, для которой токи в ветвях записывают со знаком плюс, если их направление совпадает с направлением обхода контура: