
§ 5.3. Составление уравнений электрической схемы в матричной форме
Матричное уравнение контурных токов. 1. В исходной схеме нумеруют узлы, элементы ветвей и выбирают положительные направления токов в ветвях. Если ветви схемы содержат только идеальные источники, то их преобразовывают. 2. Граф схемы изображают с той же нумерацией узлов и ветвей, что и в схеме. 3. Выбирают дерево графа. По ветвям связи графа определяют независимые контуры, которые затем нумеруют. Выбирают направление обхода контуров. 4. Составляют контурную матрицу Β. 5. Составляют матрицу сопротивлений ветвей Ζв. В случае получения сложных матриц Β и Ζв их разбивают на подматрицы ΒL, ΒС, ΒR, ΖвL, ΖвС и ΖвR. 6. Матрицу контурных сопротивлений находят по выражению
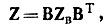
где ΒТ - транспонированная контурная матрица (в матрице Β строки и столбцы поменялись местами). Тройное матричное произведение ΒΖвΒT является определителем системы:
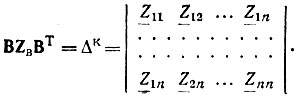
7. Составляют матрицы E и J и записывают уравнение для схемы:
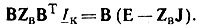
Матричное уравнение узловых потенциалов. 1. В исходной схеме нумеруют узлы и ветви. Выбирают базисный узел. 2. Граф схемы изображают с той же нумерацией узлов и ветвей, что и в схеме. 3. Составляют узловую матрицу Α, которую при необходимости разбивают на подматрицы ΑL, ΑC и ΑR. 4. Составляют матрицу проводимостей ветвей Υв, которую при необходимости разбивают на подматрицы ΥвL, ΥвC и ΥвR. 5. Матрицу узловых проводимостей находят по выражению
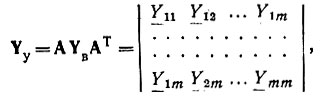
где ΑТ - транспонированная узловая матрица. 6. Составляют матрицы э. д. с. Ε и токов источников тока J и записывают уравнение для схемы: 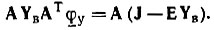

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
