
§ 5.4. Нахождение определителя схемы по топологическим формулам
1. Определитель матрицы узловых проводимостей Δ(у) равен сумме произведений проводимостей ветвей всех деревьев графа схемы:
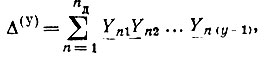
где nд - число всех деревьев графа;  - произведение проводимостей ветвей n-го дерева графа.
- произведение проводимостей ветвей n-го дерева графа.
Если проводимость каждой ветви схемы принять равной единице, то узловой определитель равен числу деревьев графа: 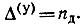
2. Определитель матрицы проводимостей сечений равен определителю проводимостей ветвей:
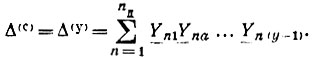
Рассмотрим упрощенные методы вычисления определителя такие, как разложение определителя по узлу или по путям между двумя узлами.
Разложение определителя по узлу. Если к выбранному узлу m подходит n ветвей с проводимостями a1, a2, ..., an, то определитель
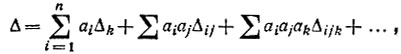
где Δk - определитель, получающийся из определителя исходной схемы закорачиванием ветви ak и размыканием всех остальных ветвей, сходящихся в узле; 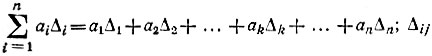 - определитель, получающийся из определителя исходной схемы закорачиванием ветвей и ау и размыканием всех остальных ветвей, подходящих к узлу (равен сумме произведений проводимостей всех деревьев образованного графа);
- определитель, получающийся из определителя исходной схемы закорачиванием ветвей и ау и размыканием всех остальных ветвей, подходящих к узлу (равен сумме произведений проводимостей всех деревьев образованного графа); 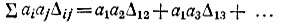
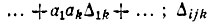 - определитель, получающийся из определителя исходной схемы при одновременном закорачивании ветвей i, j, ..., k и размыкании остальных ветвей, подходящих к узлу. При закорачивании всех ветвей определитель равен единице.
- определитель, получающийся из определителя исходной схемы при одновременном закорачивании ветвей i, j, ..., k и размыкании остальных ветвей, подходящих к узлу. При закорачивании всех ветвей определитель равен единице.
Пример. Для графа рис. 5.9 разложить определитель Δ по узлу I.
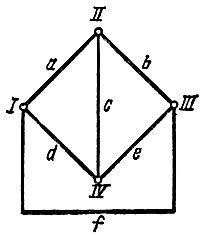
Рис. 5.9
Решение. К узлу I подходят три ветви a, d и f, поэтому определитель, разложенный по выбранному узлу,
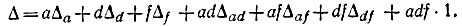
В каждое слагаемое этого равенства входят определители соответствующих подграфов.
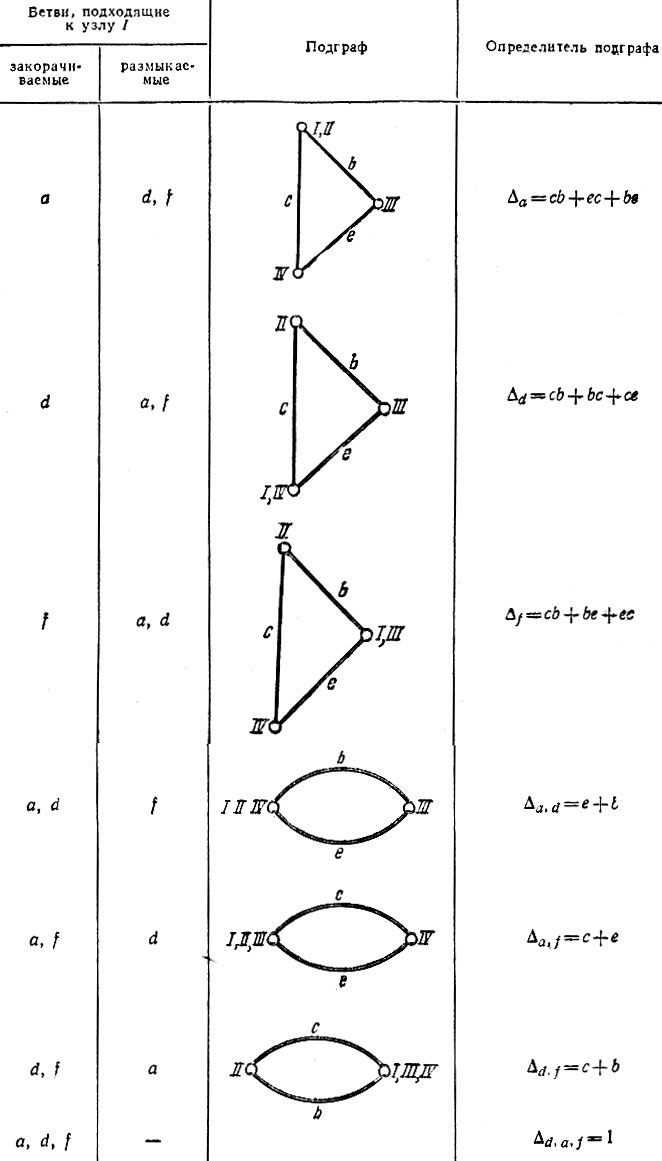
Разложение определителя по узлу
Определитель схемы
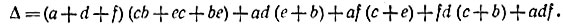
Разложение определителя по путям между двумя узлами. Выбирают два узла и устанавливают все пути между ними. Тогда определитель
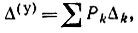
где Pk - величина k-го пути, равная произведению проводимостей всех ветвей этого пути; Δk - алгебраическое дополнение пути, получаемое из определителя схемы при коротком замыкании всего пути и равное сумме произведений проводимости ветвей всех деревьев.
Суммирование выполняют по всем возможным ветвям между выбранными деревьями и узлами.
Если замыкаются накоротко все узлы, которые входят в рассматриваемый путь, то Δk = 1.
Пример. Найти определитель Δ разложением по путям между I и III узлами графа рис. 5.9.
Решение. Между узлами I и III возможны пять путей: ab, de, f, ace и dcb, каждому из которых соответствует подграф. Для каждого подграфа находят свой определитель Δk, после чего получают определитель исходной схемы 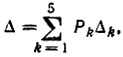
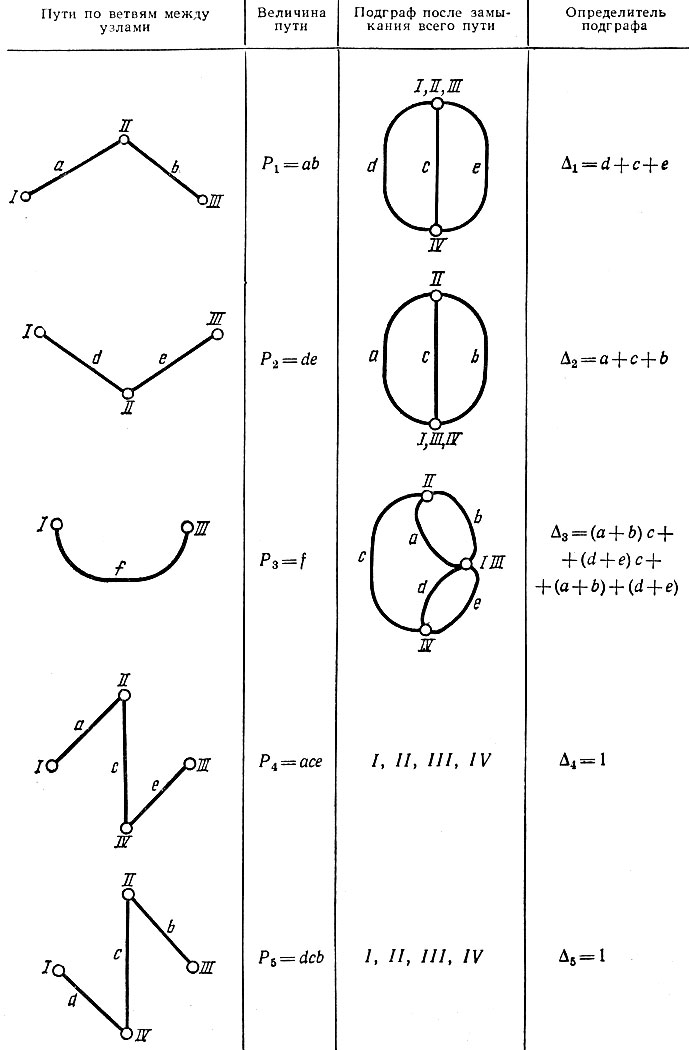
Разложение определителя по путям между двумя узлами
Таким образом, определитель схемы
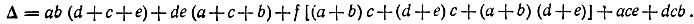

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
