§ 8.7. Начальные условия (начальные значения токов и напряжений при t = 0)

Независимые начальные условия - значения тока (потока) в индуктивном и напряжения (заряда) на емкостном элементах в момент коммутации (t = 0), определяемые по законам коммутации.

Зависимые начальные условия - значения токов и напряжений в момент коммутации (t = 0₊), определяемые по схеме, образованной после коммутации по законам Кирхгофа с учетом законов коммутации. Схема имеет нулевые начальные условия, если в момент коммутации (t = 0) токи и напряжения на всех ее пассивных элементах равны нулю (i_L(0) = 0, u_С(0) = 0).

При нулевых начальных условиях наличие индуктивного элемента равносильно разрыву ветви [i_L(0_-) = 0], а емкостного - короткому замыканию [u_С(0_-) = 0]. Постоянные интегрирования, число которых равно порядку уравнения n, определяют по зависимым и независимым начальным условиям. При этом вычисляют значение искомой переходной функции и ее (n - 1)-ю производную в момент коммутации t = 0.

Найдем независимые и зависимые начальные условия для схемы рис. 8.3 (E = const).

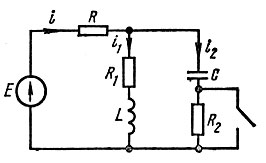
Рис. 8.3

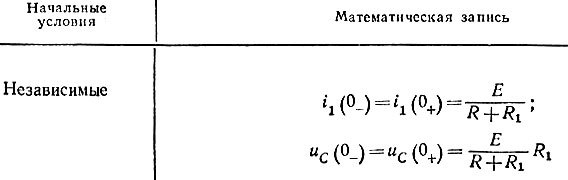
Начальные условия (начальные значения токов и напряжений при t = 0)

Начальные условия (начальные значения токов и напряжений при t = 0)