§ 8.12. Операторный метод

С помощью преобразования Лапласа совершается переход от дифференциально-интегральных уравнений электрической схемы искомой переходной функции - оригинала к алгебраическим уравнениям в изображениях.

Решение системы алгебраических уравнений дает изображение искомой функции, оригинал которой может быть получен путем использования обратного преобразования Лапласа.

Оригиналом f(t) называют функцию времени, например, i(t), u(t), e(t), Q(t), Ψ(t).

Изображением оригинала F(p) называют функцию комплексной переменной p = a + jb, например I(р), U(р), Е(р), Q(p), Ψ(р).

Соответствие между изображением (оригиналом) и оригиналом (изображением) записывают следующим образом:

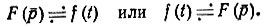
Операторный метод