
§ 8.32. Составление дифференциальных уравнений состояния с помощью уравнений Кирхгофа
1. Выбирают переменные состояния. Обычно это токи в индуктивных iL и напряжения на емкостных uС элементах.
2. Составляют дифференциальное уравнение для производных от переменных состояния. Применяя уравнения Кирхгофа для послекоммутационной схемы, решают их относительно производных переменных состояния diL/dt = iL и duC/dt = uC в зависимости от iL, uС и источников энергии en. Уравнение состояния записывают в матричной форме:
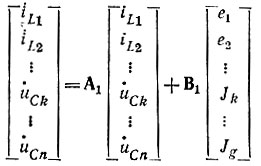
или 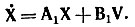
3. Составляют алгебраическое уравнение для выходных (искомых) переменных. Рассматривая послекоммутационную схему, находят уравнения, связывающие выходные (искомые) переменные (токи в ветвях ik и напряжения на элементах uk) и переменные состояния. Полученные уравнения записывают в матричной форме:
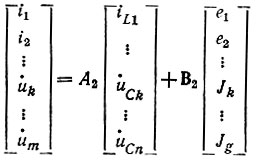
или 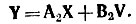
Пример. Получить уравнения состояния для определения выходных переменных тока i и напряжения u1 с помощью законов Кирхгофа в послекоммутационной схеме рис. 8.10.
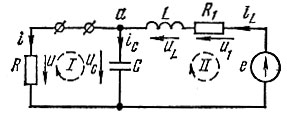
Рис. 8.10
Решение. За переменные состояния примем iL и uС. По законам Кирхгофа для узла а и контуров I и II получим уравнения производных состояния:
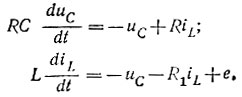
Запишем эти уравнения в матричной форме:
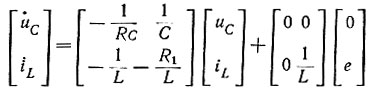
или 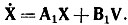
Уравнения, связывающие выходные (искомые) переменные и переменные состояния (iL и uC), получим исходя из схемы рис. 8.10:
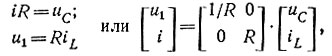
т. е. 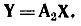

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
