
§ 8.33. Составление дифференциальных уравнений состояния методом наложения
1. Выбирают переменные состояния. Как правило, это токи в индуктивных iL и напряжения на емкостных uС элементах.
2. В послекоммутационной схеме все индуктивные и емкостные элементы выделяют так, чтобы оставшаяся часть схемы содержала только резистивные элементы, источники э. д. с. и токов (рис. 8.11).
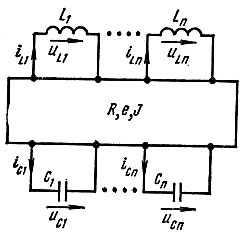
Рис. 8.11
Для каждого индуктивного и емкостного элементов записывают выражения для напряжения и тока
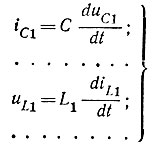
или в матричной форме
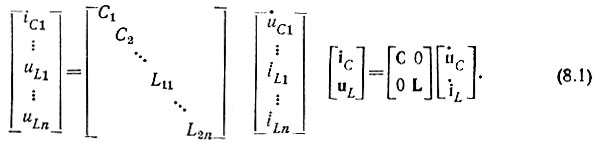
3. Записывают систему линейных алгебраических уравнений для переменных состояний iLk и uCk и внешних воздействий e и J, применяя принцип наложения:
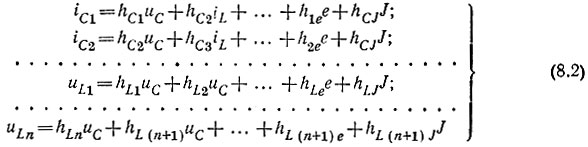
4. В зависимости от переменных состояния и внешних воздействий составляют уравнения для выходных переменных, например для тока в какой-либо ветви i и для напряжения на заданном элементе:
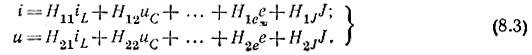
5. Коэффициенты h, Н находят исходя из уравнений (8.2) и (8.3), а также схемы, рис. 8.12, полученной из послекоммутационной схемы рис. 8.11, в которой вместо индуктивных элементов включены источники тока iLk, а вместо емкостных - источники э. д. с. uCk.
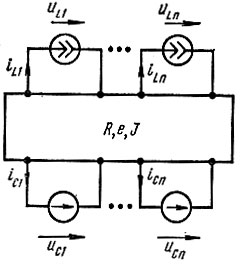
Рис. 8.12
В полученной схеме поочередно оставляют один источник (остальные источники э. д. с. закорачивают, а источники тока размыкают).
В уравнениях для переменных состояния (8.2) и выходных переменных (8.3) учитывают только слагаемое, определяемое этим источником. При этом в правых частях уравнений (8.2) и (8.3) остается только по одному члену.
Схему с одним источником рассчитывают так, чтобы иметь соотношения, аналогичные соотношениям между переменными, оставшимися в уравнениях.
Коэффициенты h и Н находят путем сравнения уравнений, полученных при расчете схемы, и новых уравнений для переменных состояния и выходных переменных. После чего записывают в матричной форме:
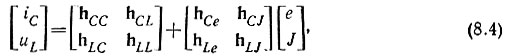
где h - матрицы, определяющие связь между соответствующими переменными в схеме рис. 8.13.
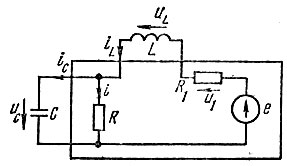
Рис. 8.13
Сравнивая уравнения (8.1) и (8.4), получают матричное уравнение типа 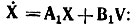
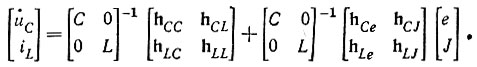
7. В уравнение для выходных переменных (8.3) подставляют найденные коэффициенты и записывают его в матричной форме: 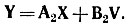
Пример. Получить уравнения переменных состояния схемы рис. 8.13 методом наложения.
Решение. В качестве переменных состояния выбираем iL и uС.
Выделим в схеме рис. 8.13 индуктивный и емкостный элементы.
Запишем выражения для напряжения на индуктивном и тока в емкостном элементах:
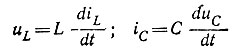
или в матричной форме:

Запишем алгебраические уравнения для iC и uL в общем виде:
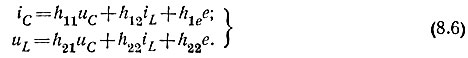
Уравнения для выходных переменных имеют вид:
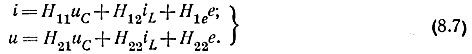
Коэффициенты в уравнениях (8.5) и (8.7) определяют, применяя метод наложения и исходя из схемы рис. 8.14 и уравнений (8.6) и (8.7).
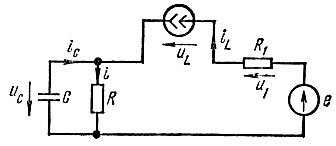
Рис. 8.14
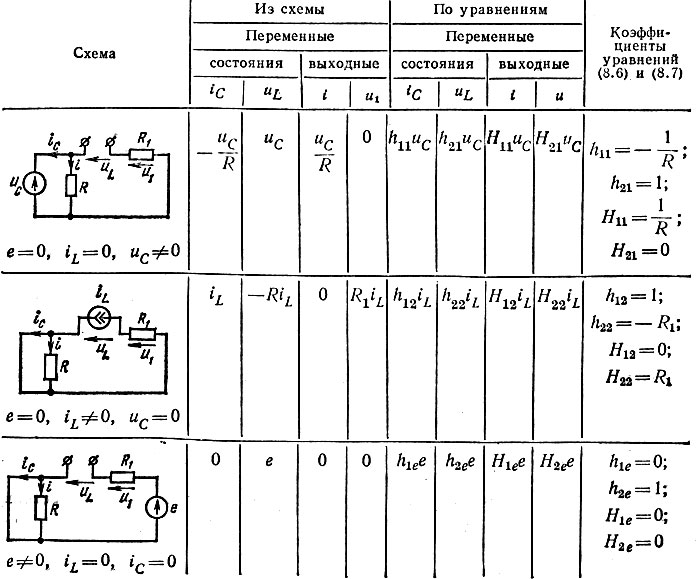
Таким образом, в уравнениях (8.6) и (8.7) коэффициенты определены. Уравнение (8.6) примет вид:
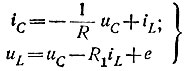
или
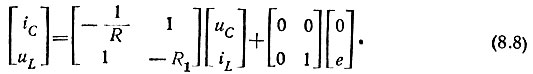
Сравнивая матричные уравнения (8.5) и (8.8), получим
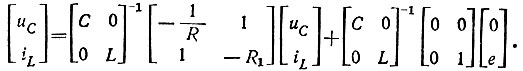
Имея в виду что 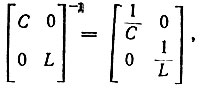 определим
определим
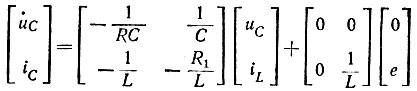
или 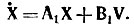
Подставим в уравнение (8.7) найденные коэффициенты. Тогда
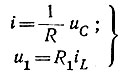
или
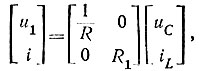
т. е.
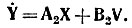

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
