§ 11.6. Разложение по Фостеру мнимой входной функции Z(p)

Пример. Реализовать функцию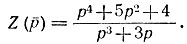

Решение. Заданная функция имеет признаки чисто мнимой функции (числитель имеет четные степени р, а знаменатель нечетные; степени числителя и знаменателя отличаются на единицу), следовательно, ее полюсы и нули лежат на мнимой оси и чередуются. Такая функция реализуется LC-двухполюсниками. Разложим 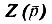на простые дроби по первой форме Фостера:

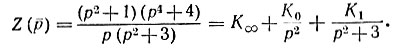
Целая часть К_∞ = 1 получена выделением полюса в бесконечности. Коэффициент K₀ определяется вычетом в полюсе р = 0:

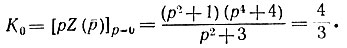
Определяя вычет в полюсах 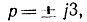получим

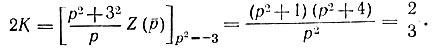
Таким образом, функция сопротивления разложена на простые дроби:

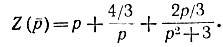
Каждое слагаемое в 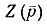реализуется соответствующим реактивным двухполюсником (рис. 11.1).

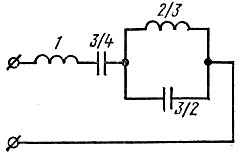
Рис. 11.1