§ 11.9. Разложение входной функции в непрерывную дробь (реализация двухполюсников по Кауэру)

Заданную дробно-рациональную функцию, например,

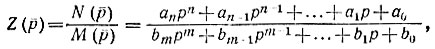
раскладывают в непрерывную дробь путем деления числителя на знаменатель. Деление проводят до тех пор, пока полученный остаток можно реализовать схемой известного двухполюсника. В результате схема имеет цепную структуру, последним звеном в которой является двухполюсник, реализующий остаток.

Реализующие схемы, соответствующие входной функции, зависят от того как располагаются полиномы в числителе и знаменателе по возрастающим или убывающим степеням.

Если многочлен числителя функции расположен по возрастающим степеням и степень многочлена числителя больше степени многочлена знаменателя (при р = ∞ функция имеет полюс), то для ее реализации применяют первую форму реализации Кауэра. Путем деления многочлена числителя на многочлен знаменателя выделяют полюс L₁p и остаток 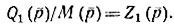Полюс реализуют последовательной индуктивностью, а в дроби, обратной дроби остатка 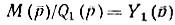выделяют полюс (делением числителя на знаменатель), который реализуют параллельной емкостью. Из обратной дроби нового остатка выделяют полюс и т. д.

В результате такого деления получают конечную непрерывную дробь

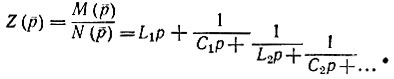
Этой дроби соответствует реализующая схема рис. 11.4, а.

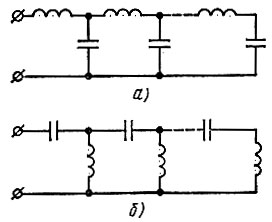
Рис. 11.4

Если многочлены функции расположены по убывающим степеням и функция имеет полюс в нуле, то для ее реализации применяют вторую форму реализации Кауэра. Путем деления многочлена числителя на многочлен знаменателя (начиная с младших степеней) выделяют первый полюс в нуле, второй полюс выделяют делением знаменателя остатка на его числитель и т. д.

Такой процесс последовательного деления приводит к непрерывной дроби вида

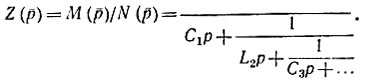
Реализующая схема (рис. 11.4, б) на входе содержит последовательно включенный емкостный элемент.

Пример. Реализовать функцию 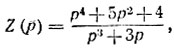применяя первую и вторую формы реализации Кауэра.

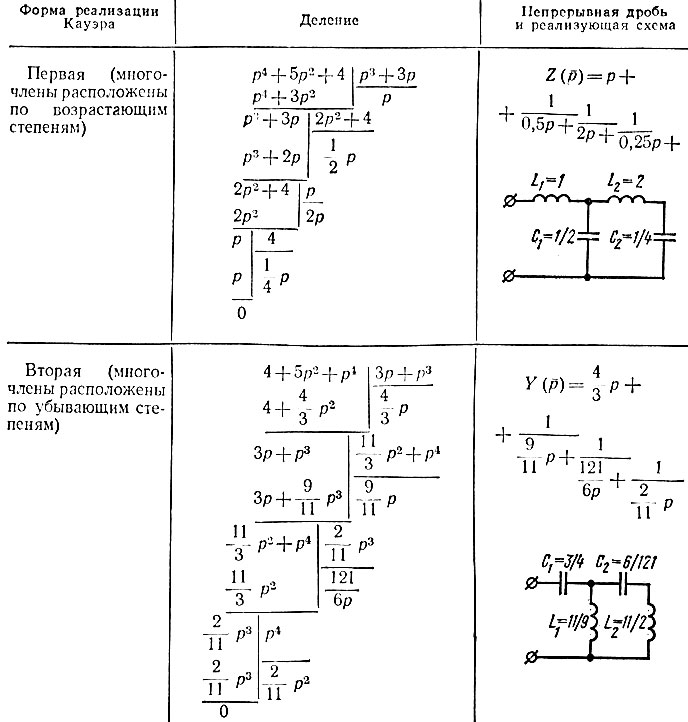
Решение.