
§ 14.6. Определение коэффициентов аппроксимирующей функции
В этом параграфе рассматриваются методы выбранных точек и метод наименьших квадратов.
Метод выбранных точек. На нелинейной характеристике выбирают точки, через которые будет проходить аппроксимирующая кривая. Выбранные точки должны лежать в рабочей области и в характерных точках в. а. х. Число таких точек равно числу определяемых коэффициентов аппроксимирующей функции. Координаты точек подставляют в аппроксимирующее выражение. Полученную систему уравнений решают относительно искомых коэффициентов.
Данный метод является трудоемким, особенно при аппроксимации с помощью трансцендентных функций (например, y = ashβx). Он не гарантирует совпадения аппроксимирующей кривой и рассматриваемой характеристики вне выбранных точек.
Пример. Аппроксимировать нелинейную характеристику рис. 14.1 степенным полиномом y = a0 + a1х + a2x2 в рабочем диапазоне ab.
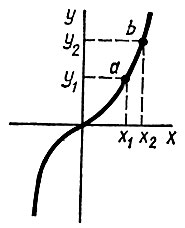
Рис.14.1
Решение. Выберем точки с координатами 0, 0; хqy1; х2у2. В нашем случае
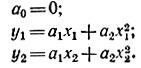
Из этих уравнений находят коэффициенты a1 и a2.
Метод наименьших квадратов. Этот метод основан на составлении выражения для минимума отклонения среднеквадратичной ошибки от исходной кривой в выбранных точках. Коэффициенты аппроксимирующей функции выбирают так, чтобы квадратичная ошибка 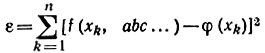 была минимальна, где f(xk, abc) - аппроксимирующая функция; φ(xn) - экспериментальная характеристика, которая аппроксимируется; х1х2 ... хk - произвольно выбранные аргументы (от нуля до максимального значения) в рабочем диапазоне экспериментальной характеристики.
была минимальна, где f(xk, abc) - аппроксимирующая функция; φ(xn) - экспериментальная характеристика, которая аппроксимируется; х1х2 ... хk - произвольно выбранные аргументы (от нуля до максимального значения) в рабочем диапазоне экспериментальной характеристики.
Системы уравнений для определения коэффициентов получают путем приравнивания к нулю частных производных от ε по всем коэффициентам:
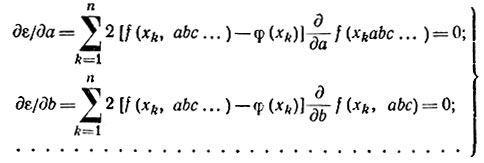
Пример. Методом наименьших квадратов найти коэффициенты полинома y = f(x) = a0 + a1x + a2x2, аппроксимирующего некоторую характеристику, заданную табл. 14.1.
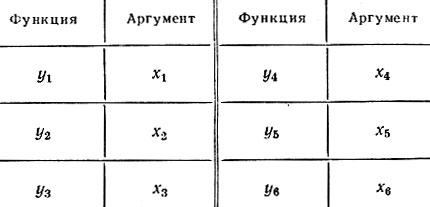
Таблица 14.1
Решение. Образуя частные производные от среднеквадратичной ошибки, получим систему алгебраических уравнений относительно искомых уравнений.
Выберем три точки на экспериментальной характеристике с аргументами, например, х1, х4 и х6. Тогда
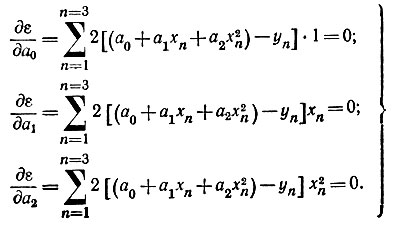

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
