
§ 17.2. Метод линейной аппроксимации
При расчете характеристику нелинейного элемента заменяют прямой, проходящей через точку с координатами, соответствующими установившемуся режиму. Уравнение прямой подставляют в дифференциальное уравнение схемы и получают линейное дифференциальное уравнение.
Найденное приближенное решение линейного уравнения уточняют по заданной нелинейной характеристике. Этот метод используют для ориентировочных расчетов.
Пример. Определить переходный ток i(t), возникающий при подключении нелинейного индуктивного элемента к источнику постоянного напряжения (рис. 17.1, а).
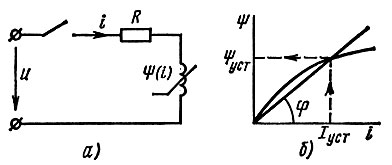
Рис. 17.1
Решение. Составим уравнение по второму закону Кирхгофа:
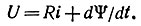
В установившемся режиме (t → ∞) ток i = Iуст = U/R. По кривой Ψ(i) (рис. 17.1, б) определим значение соответствующее Iуст. Через начало координат и точку на кривой (Ψуст, Iуст) проводим прямую Ψ = i tg φ = Ψуст/Iустi. Полученное выражение подставим в исходное дифференциальное уравнение:
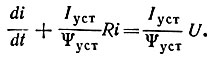
Имеем линейное дифференциальное уравнение первого порядка. Его решение:
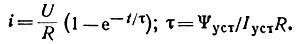

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
