§ 18.5. Устойчивость в малом

Состояние равновесия называют устойчивым, если при любой заданной области ε допустимых отклонений от состояния равновесия существует область δ, окружающая область состояния равновесия так, что ни одно движение, начинающееся в области δ, никогда не достигнет границ области ε (рис. 18.3).

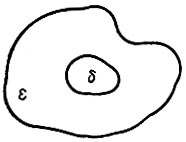
Рис. 18.3

Задав область ε малой, получим еще меньшую область δ. Область начальных условий δ определяет область ε.

Устойчивость в малом может быть определена по Ляпунову анализом упрощенных линеаризованных уравнений в окрестности исследуемой точки. При этом об устойчивости судят по корням характеристического уравнения.