2. Моделирование процесса обучения

Моделирование в системах автоматического управления процесса выработки условных рефлексов имеет первостепенное значение для создания самообучающихся систем.

Как известно, Павлов показал, что если достаточно часто перед кормлением животного подавать звуковой сигнал, например включать звонок, то, начиная с некоторого времени, животное будет реагировать на этот сигнал так же, как и на пищу, т. е. при появлении звукового сигнала у животного начнется выделение слюны.

Рассмотрим процесс моделирования этого опыта в простейшей электрической схеме, показанной на рис. 7.2.

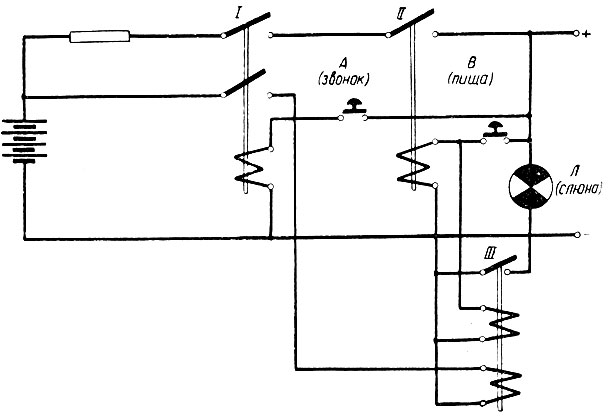
Рис. 7.2. Схема моделирования

Как следует из этой схемы, вначале при включении кнопки А, соответствующей появлению сигнала "звонок", лампа, сигнализирующая о появлении "слюны", не загорается, ибо при этом включается только переключатель I (аккумулятор не заряжен). Если же нажать кнопку В ("дать пищу"), то включается переключатель III и загорается сигнальная лампа.

Попробуем теперь нажимать одновременно на кнопки А и В (при подаче "пищи" включать "звонок"). При каждом таком нажатии одновременно включаются переключатели I и II и подзаряжается аккумулятор. Наконец, после многократных повторений аккумулятор настолько зарядится, что при включении только кнопки А (включение звонка) будет включаться и переключатель III, т. е. загораться сигнальная лампа.

Однако такое положение, не будет продолжаться бесконечно долгое время. Если несколько раз подряд нажимать только кнопку A, то аккумулятор разрядится. После этого схема вновь перестанет реагировать на сигнал A.

Таким образом, схема, показанная на рис. 7.2, позволяет моделировать процесс выработки условного рефлекса и поэтому является элементом самообучающейся системы. Действие этой системы основано на определении вероятности совпадения событий А и В. Если эта вероятность велика, то аккумулятор постепенно заряжается. Если же вероятность совпадения событий мала, то аккумулятор не заряжается (или даже разряжается).

Рассмотрим (рис. 7.3) еще одну схему, выполненную на основе логических элементов.

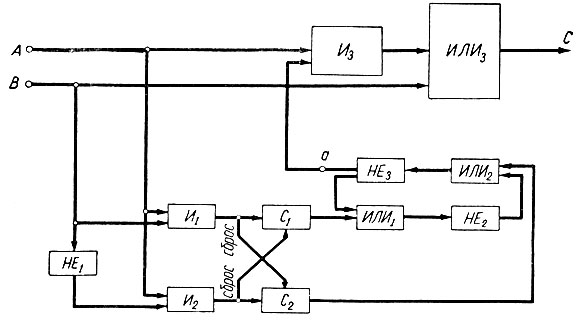
Рис. 7.3. Схема на логических элементах

Схема имеет два входа (А и В), на которые периодически включаются напряжения (аналогично тому, как в схеме рис. 7.2 нажимались кнопки А и В). Благодаря наличию логического элемента И₁ счетчик С₁ ведет подсчет количества случаев одновременного появления сигналов А и В (аналогично тому, как в схеме 7.2 при нажатии обеих кнопок заряжалась батарея). В противоположность этому счетчик С₂ подсчитывает, сколько раз появляется напряжение на входе А при его отсутствии на входе В (аналогия разряду батареи в схеме рис. 7.2).

Счетчик C₁ устроен так, что после n₁ импульсов, поданных на его вход, на его выходе появляется сигнал. Аналогично этому сигнал на выходе счетчика С₂ появляется после n₂ сигналов на его входе. Кроме того, каждый из счетчиков сбрасывается на нуль после появления сигнала на входе другого счетчика.

Выходы счетчиков включаются на триггер, состоящий из четырех логических элементов (ИЛИ₁, НЕ₂, ИЛИ₂, НЕ₃). Причем, как видно из схемы, счетчик С₁ записывает в точке a единицу, а счетчик С₂ - стирает ее.

Работает схема следующим образом. Каждый раз, когда сигналы А и В появляются одновременно, срабатывает логический элемент И₁, а счетчик С₁ подсчитывает число этих срабатываний. Когда это число достигает n₁, счетчик дает сигнал на вход триггера и в точке а появляется единица.

Вначале, если на вход схемы подать только сигнал А, то на ее выходе будет нуль. Однако, после того как в точке a появилась единица, при появлении только сигнала А (как и при одновременном появлении сигналов A и В) на выходе (С) схемы появится единица.

Если хоть один раз сигнал А появится без сигнала В, то сработают элементы НЕ₁, И₂ и сбросят на нуль показания счетчика С₁. Одновременно счетчиком С₂ начинается подсчет количества случаев, когда сигнал А появляется без сигнала В. Если это количество достигнет n₂, то появится сигнал на выходе счетчика С₂, триггер сработает и в точке а вновь появится нуль. После этого при наличии сигнала только на входе А сигнал (С) на выходе схемы не появится.

Если во время подсчета числа сигналов счетчиком С₂ появится импульс на входе счетчика С₁, то показания счетчика будут сброшены на нуль. Таким образом, схема, показанная на рис. 7.3, работает аналогично схеме, изображенной на рис. 7.2.

Следует отметить, что схема рис. 7.3, как и предыдущая схема, в зависимости от вероятности одновременного появления сигналов А и В меняет свою логическую схему. Действительно, как следует из рис. 7.3, при малой вероятности одновременного появления сигналов А и В схема выполняет логическое суждение

Однако при большой вероятности одновременного появления этих сигналов схема уже выполняет другое логическое суждение

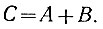
Схемы, показанные на рис. 7.2 и 7.3, являются основными элементами, на основе которых могут строиться сложные самообучающиеся системы автоматического управления.

Рассмотрим один из простейших примеров применения схемы, показанной на рис. 7.3. Предположим, что перед нами поставлена задача автоматизации регулирования глубины резания при проточке на токарном станке цилиндрической детали. Резец в этом станке может быть установлен так, что обрабатываемая деталь будет протачиваться до нужного диаметра. Однако по мере того как резец истирается, диаметр обрабатываемых деталей постепенно увеличивается, пока, наконец, не появятся бракованные детали, диаметр которых превышает допустимую величину. Чтобы этого не случилось, нужно по мере истирания резца передвигать его в направлении центра вращающейся детали.

Вместе с тем следует иметь в виду, что различные детали оказывают в режиме резания разное сопротивление резцу. Это происходит потому, что попадаются детали разных плавок, имеющие различную коррозийную корку, и т. д. Поэтому из-за наличия люфтов и пружинящих свойств системы крепления резца величина диаметра готовой детали становится случайной. Тогда увеличение диаметра одной (k-ой) детали по сравнению с предыдущей (k-1) не может служить сигналом необходимости передвижения резца, ибо диаметр следующей детали (k+1) может оказаться меньшим, чем диаметр данной детали.

Следовательно, резец необходимо передвигать тогда, когда вероятность того, что диаметр детали увеличился из-за притупления резца, станет достаточно большой.

Поэтому, использовав принцип схемы рис. 7.3, создадим следующую схему автоматического управления резцом станка (рис. 7.4).

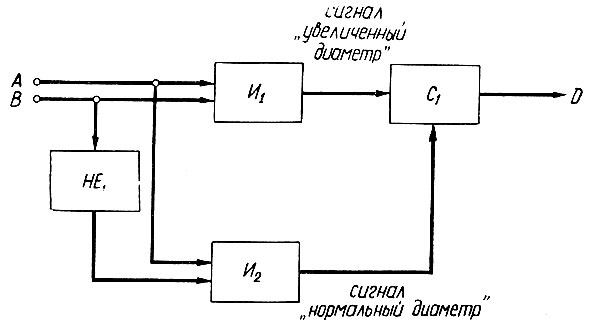
Рис. 7.4. Логическая схема управления шаговым двигателем

На вход этой схемы подается два сигнала: сигнал (A) об изготовлении детали и сигнал (В) о том, что диаметр изготовленной детали оказался больше заданной величины. Причем эта величина выбирается менее допустимой (максимальной), с таким расчетом, чтобы случайное увеличение диаметра детали не приводило к браку.

Таким образом, на выходе элемента И₁ сигнал появляется всякий раз, когда диаметр детали оказывается большим, нежели заданная величина. Счетчик С₁ подсчитывает число таких деталей и дает сигнал в том случае, когда их число, как и в схеме рис. 7.3, достигло n₁.

Сигнал на выходе элемента И₂ появляется тогда, когда диаметр измеренной детали не превышает заданной величины. Этот сигнал сбрасывает показания счетчика С₁ на нуль.

Следовательно, сигнал на выходе счетчика сообщает о том, что вероятность появления деталей с увеличенным диаметром стала достаточно высокой. Этот сигнал подается на шаговый искатель, который делает шаг и, поворачивая винт подачи резца, передвигает его на заданное расстояние.

В этой задаче, естественно, предполагается, что расстояние, на которое передвигается резец при одном шаге искателя, оказывается достаточным для того, чтобы диаметр деталей после этого передвижения стал меньше заданной величины.

Рассмотрим пример, в котором исследуемый сигнал имеет непрерывную форму.

Предположим, что перед нами поставлена следующая задача. Имеется (рис. 7.5) две аккумуляторные батареи, одна из которых работает в режиме заряда, а другая - в режиме разряда. Переключение батарей из одного режима в другой осуществляется при помощи двухконтактного шагового искателя. Необходимо обеспечить переключение разряжающейся батареи на заряд в том случае, когда ее напряжение снизится до определенного предела, и включить вместо нее другую батарею, которая до этого работала в режиме заряда.

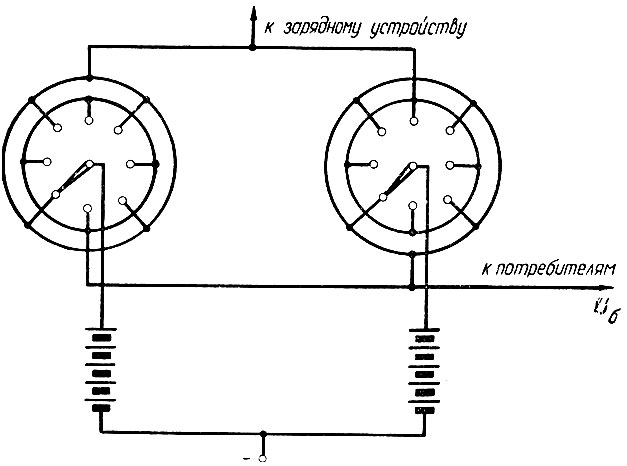
Рис. 7.5. Схема переключения аккумуляторных батарей

Следует иметь в виду, что батарея имеет большое количество потребителей, характеристики и график работы которых в большинстве случаев неизвестны. Кроме того, при включении электродвигателей происходит кратковременная посадка напряжения батареи. Поэтому напряжение батареи (рис. 7.6) является случайной функцией времени.

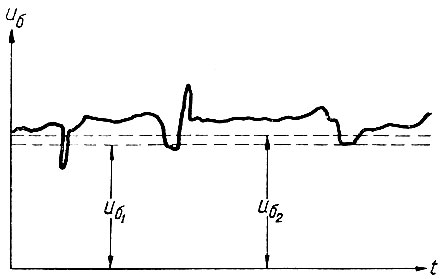
Рис. 7.6. Напряжение батареи

Следовательно, в рассматриваемом примере нельзя, как это делается в обычных системах регулирования по отклонению, осуществлять переключение аккумуляторных батарей в тот момент, когда напряжение разряжающейся батареи достигло какого-либо минимального значения.

Поэтому, воспользовавшись принципом схемы рис. 7.2, используем для переключения батареи схему, показанную на рис. 7.7.

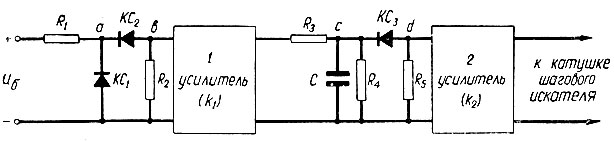
Рис. 7.7. Схема управления переключателем аккумуляторной батареи

Принцип работы отдельных элементов этой схемы показан на рис. 7.8. Первый элемент (рис. 7.8, а), состоящий из сопротивления R₁ и кремниевого стабилотрона КС₁, срезает те части непрерывной кривой напряжения u_б, в которых это напряжение превосходит величину u_б2.

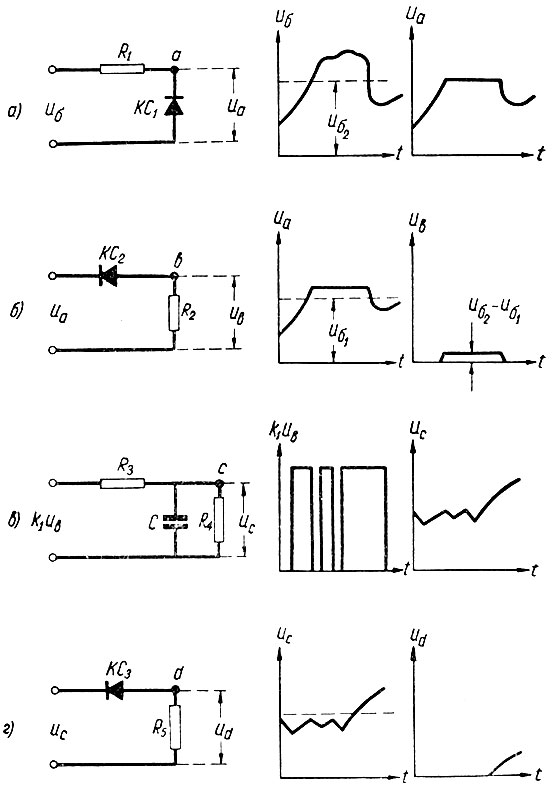
Рис. 7.8. Логические преобразования

Второй элемент (рис. 7.8, б), образуемый стабилотроном КС₂ и сопротивлением R₂, как бы снимает верхнюю площадку напряжения u_а (возвышающуюся над u_б1) и опускает ее к оси абсцисс (напряжение u_b).

Благодаря этому на вход первого усилителя подаются почти прямоугольные импульсы. Отношение времени наличия этих импульсов к общему времени измерения определяет вероятность того, что напряжение аккумуляторной батареи находится в диапазоне u_б2 > u_б > u_б1.

Для управления шаговым искателем схемы рис. 7.5 нет необходимости в нахождении указанной вероятности. В этом случае достаточно определить момент, когда вероятность (Р) достигнет заданной величины (P₁). Поэтому далее проделаем следующее.

Усилим напряжение u_b и подадим его на элемент, состоящий (рис. 7.8, в) из емкости (С) и двух сопротивлений (R₃ и R₄). Легко увидеть, что при наличии напряжения на выходе этого элемента емкость заряжается, а при отсутствии напряжения - разряжается (через сопротивление R₄). Поэтому заданная величина вероятности (P₁) может характеризоваться напряжением (u_С) на выходе рассматриваемого элемента.

Следовательно, срезав при помощи элемента, показанного на рис. 7.8, г, нижнюю часть кривой u_C = f(t), получим напряжение (u_d), сигнализирующее о том, что вероятность нахождения напряжения аккумуляторной батареи в диапазоне u_б2 > u_б > u_б1 превысила заданную величину (P₁). Если теперь напряжение u_d усилить и подать на катушку шагового искателя, то можно осуществить поставленную задачу автоматического переключения батареи в режим заряда.

В настоящее время исследование самообучающихся систем с целью их применения в различных отраслях народного хозяйства только начинается. Поэтому существующие системы автоматического управления способны моделировать лишь простейшие элементы процесса обучения живых существ. Однако бурное развитие кибернетики показывает, что моделирование этого процесса с каждым годом будет становиться все более глубоким. И нет никакого сомнения в том, что в ближайшем будущем самообучающиеся системы найдут себе чрезвычайно широкую область применения.

Из-за сравнительно небольшого объема этой книги, естественно, нельзя было охватить все многообразие вопросов и задач, выдвигаемых технической кибернетикой.

Однако это и и не являлось целью книги. Если же читатель, прочтя эту книгу, заинтересовался технической кибернетикой и получил подготовку, позволяющую ему приступить к применению кибернетики в решении практических задач и изучению специальной научной литературы, то автор считает свою задачу выполненной.