Глава четвертая. Побочные составляющие и шумы в системах ДКСЧ СВЧ диапазона

4.1. Умножение частоты колебаний, содержащих побочные составляющие

Как следует из структурной схемы устройства с диапазонно-кварцевой стабилизацией частоты, в МОЧ частота эталона f_q0 подвергается многократным умножению и делению. При этом в выходных колебаниях МОЧ неминуемо должны присутствовать побочные составляющие, кратные частоте f_q0. Эти колебания, хотя и подавляются в определенной степени в синтезаторе, но, очевидно, могут отрицательно отразиться на работе последнего. С другой стороны, их полное подавление до уровня, заданного на выходе всей системы, может привести к неоправданному усложнению МОЧ. Поэтому необходимо оптимальным образом рассчитать всю систему так, чтобы при минимальном ее усложнении обеспечить заданные выходные параметры.

Из практики известно, что при умножении частоты коэффициент гармоничности колебаний уменьшается. Рассмотрим этот вопрос подробнее. Если колебание частоты f_q0 подать на умножитель частоты, то на выходе последнего получим частотный спектр в виде

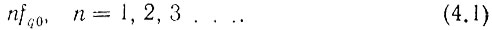
Если затем этот спектр подать на вход следующего умножителя частоты, то каждая составляющая ряда (4.1) снова умножится в любое число раз и новый ряд с точки зрения частотного распределения ничем не будет отличаться от ряда (4.1). Однако распределение амплитуд спектральных составляющих этого ряда резко изменится. Решение в общем виде данной задачи, хотя и имеет определенный теоретический смысл (такая попытка сделана в [139]), но слишком далеко от поставленного практического вопроса.

Конкретизируем задачу применительно к рассматриваемым системам. Будем считать, что после каждого каскада умножения частоты включен полосовой фильтр с монотонной характеристикой затухания. Аналогично весьма полно задача решается в [160]. Однако применительно к особенностям указанных устройств можно решить ее несколько проще. Так, будем учитывать только две побочные составляющие, ближайшие к колебанию выделяемой частоты. На рис. 4.1 изображены анализируемая структурная схема и примерный характер спектров колебаний в ее отдельных точках.

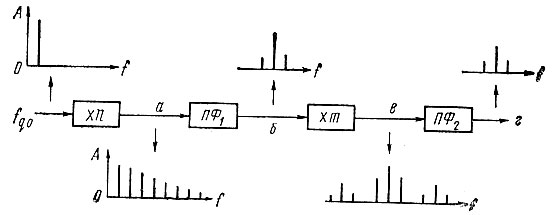
Рис. 4.1. Структурная схема двухкаскадного умножителя частоты

Рассмотрим подробнее спектры в точках схемы рис. 4.1 и механизмы их образования. На выходе первого умножительного каскада (точка а) имеем равномерный спектр (4.1) с шагом дискретности f_q0, амплитуды составляющих которого подчиняются разложению в ряд Фурье (рис. 4.2а). Однако в общем случае без конкретной характеристики нелинейного элемента невозможно выяснить количественные амплитудные соотношения ряда. Впрочем, это затруднение можно с успехом обойти, если рассматривать не сами амплитуды отдельных спектральных составляющих, а их отношения.

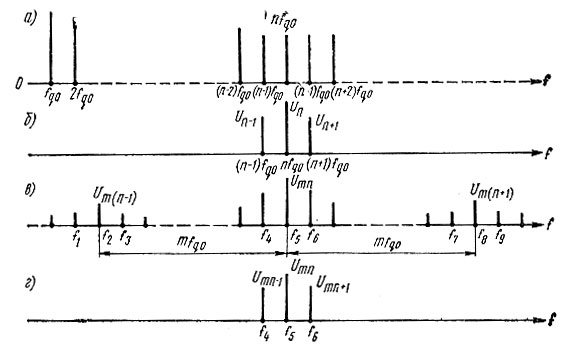
Рис. 4.2. Спектры колебаний в различных точках двухкаскадного умножителя частоты

На выходе ПФ₁ (полосового фильтра после первого умножителя частоты) в соответствии со сделанным допущением о монотонности характеристики затухания спектр можно представить тремя составляющими (рис. 4.2б). Заметим, что для удобства масштаб на отдельных графиках рис. 4.2 не сохранен.

Так как в обычных устройствах n >> 1 и степень подавления побочных составляющих велика, можно считать, что коэффициент гармоничности колебаний на выходе ПФ₁

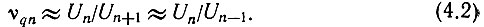
Спектр, изображенный на рис. 4.2б, математически удобно представить в виде амплитудномодулированного колебания.

На выходе второго умножительного каскада с коэффициентом умножения m получим спектр (рис. 4.2в), обязанный своим происхождением как умножению частоты, так и модуляции. Действительно, во-первых, частоты (n-1)f_q0, nf_q0 и (n+1)f_q0 умножатся на m и, во-вторых, каждое колебание этих частот (исходных и умноженных) промодулируется частотой f_q0, полученной в результате выделения на одном из нелинейных элементов умножителей, например,

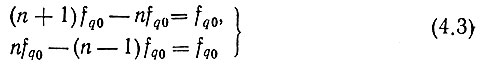
и т. д.

При этом колебания умноженных частот образуют бесконечный дискретный спектр с шагом f_q0, из которого выделим следующие, представляющие интерес колебания (рис. 4.2в) с частотами:

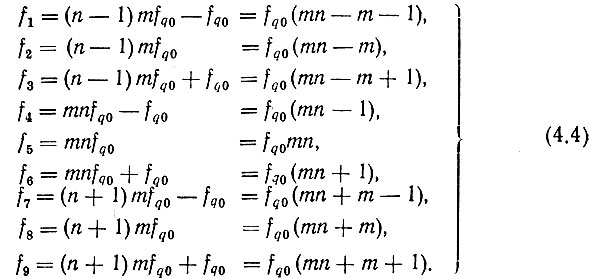
Так как амплитуды колебаний, полученных в результате второго умножения, ослабляются примерно одинаково, то 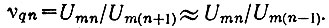После второго фильтра ПФ₂ спектр изобразится тремя составляющими (рис. 4.2г). При этом

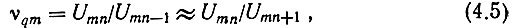
а частоты f₄, f₅ и f₆ определяются из (4.4).

При расчете системы задается коэффициент гармоничности колебаний ν_qm и по этому параметру при расчете умножителя требуется определить ν_qn. Заметим, что задача в данном случае является полной и в общем случае не только для двух-, но и многокаскадного умножителя частоты. Это легко объясняется тем, что в многокаскадном умножителе частоты подавление побочных составляющих, отстоящих от колебания умноженной частоты на величину умножаемой частоты, практически полностью осуществляется фильтром, непосредственно следующим за данным нелинейным элементом умножителя. При этом только под m следует понимать произведение коэффициентов умножения всех каскадов, следующих за рассчитываемым.

Итак, по известным ν_qm и m требуется определить коэффициент гармоничности колебаний ν_qn и характеристику затухания фильтра ПФ₁. Колебание частоты f_q0, получающееся при преобразованиях (4.3), через фильтр ПФ₁ не проходит, а модулируя U_n дает уже имеющиеся в спектре рис. 4.2б колебания U_n-1 и U_n+1. Поэтому результатом указанных преобразований в первом умножителе можно пренебречь. Итак, считаем, что на второй умножитель частоты приходят три гармонических колебания:

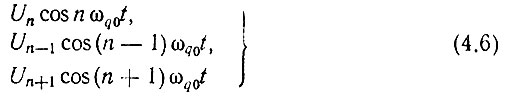
(причем фазовые соотношения этих колебаний интереса не представляют).

В пределах исследуемого интервала частот f₆-f₄ на нелинейном элементе второго умножителя частоты происходят следующие процессы: из колебаний (4.6) образуется колебание частоты f_q0; частота nf_q0 умножается на m; колебание U_mn модулируется по амплитуде с частотой f_q0.

Выделение колебания частоты f_q0 можно рассматривать как результат гетеродинного детектирования двух колебаний, например, U_n и U_n+1. В соответствии с выводами работы [140] при линейном детектировании и при U_n >> U_n+1 на нагрузке умножителя выделится напряжение

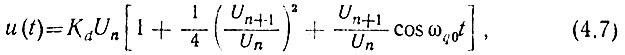
где К_d - коэффициент передачи детектора; ω_q0 = ω_q0(n + 1) - ω_q0n - разностная частота.

Напряжение разностной частоты, очевидно, является третьим слагаемым в (4.7) u_q(t) = K_dU_n+1 cos ω_q0t. Коэффициент передачи детектора зависит от соотношения сопротивления нагрузки и внутреннего сопротивления диода. После второго умножителя частоты включен полосовой фильтр со средней частотой mnf_q0. Следовательно, сопротивление нагрузки детектора и коэффициент передачи последнего являются функциями от m и n: R_н = R(m, n); K_d = К(m, n). Поэтому

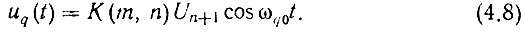
Результат умножения частоты nf_q0 на m может быть записан в виде

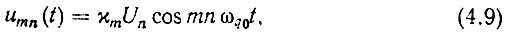
где χ_m - коэффициент передачи по напряжению второго умножителя частоты при умножении в m раз.

Из (4.9) следует, что амплитуда умноженного по частоте колебания

Рассмотрим теперь процесс модуляции напряжения (4.9) напряжением (4.8). Аналитически процесс амплитудной модуляции при помощи диодного модулятора подробно рассмотрен в [141]. Воспользуемся полученными в этой работе выводами.

Если на диодный модулятор действуют два напряжения u_mn(t) = U_mncos mnω_q0t и u_q(t) = K(m, n)U_n+1cos ω_q0t, то в токе диода наряду с другими имеется и боковая составляющая i_mn+1(t) = 0,25S'U_mnM cos(mnω_q0+ω_q0)t, где M = K(m,n)U_n+1/U_mn - коэффициент амплитудной модуляции; S' = 1/(R_iд + R_н) - динамическая крутизна характеристики модулятора; R_iд и R_н - сопротивления нелинейного элемента в рабочей точке и нагрузки.

Но R_н = R(m, n), поэтому

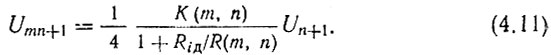
Разделив (4.10) на (4.11), с учетом (4.2) получим

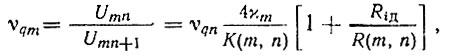
откуда искомый коэффициент гармоничности колебаний на выходе первого умножителя частоты

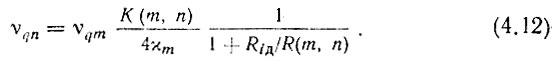
Из (4.12) следует, что с уменьшением сопротивления нагрузки для колебаний частоты f_q0 требования по селективности к фильтру, следующему за первым умножителем частоты, уменьшаются.

Однако функции R(m, n) и K(m, n) зависят от характеристик фильтра, включенного на выходе второго умножителя частоты. Так как обычно фильтры проектируют с характеристиками, обеспечиваемыми только в сравнительно узком диапазоне, вблизи частоты настройки, аналитическое задание указанных функций весьма затруднительно и, таким образом, выражение (4.12) иллюстрирует физический смысл и раскрывает качественную сторону явлений, но для количественной оценки коэффициентов гармоничности оно мало пригодно.

В работе [142] достаточно строго решается поставленная задача. Однако при этом вопрос о влиянии фильтра, включенного на выходе умножителя частоты, не рассматривается, т. е. негласно предполагается, что нагрузка умножителя частоты является апериодической. Основной вывод работы состоит в том, что коэффициент амплитудной модуляции после умножителя частоты возрастает в определенное число раз, равное коэффициенту умножения, т. е. применительно к принятым выше обозначениям

Ввиду чрезвычайной простоты выражения (4.13) представляется целесообразным его использование для практической количественной оценки необходимого дополнительного подавления побочных составляющих фильтром первого умножителя частоты по сравнению с заданным на выходе второго умножителя. При этом увеличение коэффициента гармоничности колебаний за счет селективности фильтра второго умножителя частоты будет являться определенным запасом расчета.

Выражение (4.13) можно также получить, если представить спектр, изображенный на рис. 4.2б, как результат узкополосной частотной модуляции частоты nf_q0 частотой f_q0. Боковая составляющая спектра при такой модуляции (например, [146])

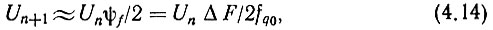
где ψ_f - индекс частотной модуляции, а ΔF - девиация частоты.

Из (4.14) имеем

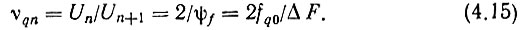
При умножении ЧМ колебаний по частоте на m, как известно, в m раз возрастает индекс модуляции из-за увеличения в m раз девиации частоты. Поэтому

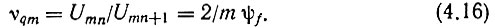
Из сопоставления (4.15) и (4.16) получаем выражение, тождественное (4.13): ν_gn = ν_qmm.

Следует отметить немаловажную роль правильного выбора диода для умножителя СВЧ. Если диод имеет значительное прямое сопротивление, то коэффициент передачи умножителя частоты будет мал, что, как следует из (4.12), уменьшает коэффициент гармоничности выходных колебаний. Этот вывод подтверждается работой [144], где рассматривается возможность усиления боковых полос на зависящем от мощности сопротивлении. В этой статье указывается, что такое усиление тем больше, чем больше отношение мощности, подаваемой на сопротивление, к мощности, снимаемой с него.

Выражение (4.13), выведенное для активного элемента в виде нелинейного сопротивления, показывает, что коэффициент гармоничности колебаний уменьшается с крутизной 6 дБ на октаву. Однако (4.13) можно распространить и на активный элемент в виде варактора. Так, в [145] делается попытка дать объяснение уменьшению коэффициента гармоничности колебаний в варакторных умножителях частоты (рассматривается частный случай для резкого p-n-перехода при постоянном смещении и большой постоянной времени цепи смещения). При этом автор получает уменьшение указанного коэффициента также 6 дБ на октаву.

В заключение отметим, что если в МОЧ осуществляется деление частоты после умножения, то выражение (4.13) останется справедливым при m < 1.