4.2. Требования к подавлению побочных составляющих в колебаниях опорных частот многодекадных синтезаторов

В гл. 2 отмечалось, что в пассивных синтезаторах необходимо подавлять побочные составляющие до необходимого уровня в местах их образования, так как от входов синтезатора к выходу полоса фильтрации расширяется. Иначе обстоит дело в активных синтезаторах с применением колец ФАПЧ, где полоса фильтрации от входов к выходу синтезатора сужается. Однако было бы неправильно всю фильтрацию осуществлять на выходе системы, так как, во-первых, при этом резко ухудшились бы другие ее характеристики, в частности, шумовые; во-вторых, при произвольных коэффициентах гармоничности колебаний опорных частот невозможно обеспечить нормальную работу колец ФАПЧ и, в-третьих, для подавления до необходимого уровня побочных составляющих, расположенных сколь угодно близко к опорным частотам, система может оказаться физически неосуществимой. Поэтому необходимо проанализировать и сформулировать требования к подавлению побочных составляющих в колебаниях опорных частот, поступающих в кольцо ФАПЧ.

Проведем такой анализ вначале для кольца аналоговой ФАПЧ. Рассмотрим эквивалентную схему (рис. 4.3) выходной декады активного многодекадного синтезатора, структурная схема которого изображена на рис. 2.7. Как видно из рисунка, из схемы исключен частотный дискриминатор, как не принимающий участия в работе в стационарном состоянии системы. При анализе будем считать УПЧ достаточно широкополосным, линейным и безынерционным, ФНЧ - пропорционально-интегрирующими с отношением постоянных времени υ > 50, УПТ - широкополосным, безынерционным с коэффициентом передачи по постоянному току К_УПТ (инерционность УПТ здесь отнесем к ФНЧ). Указанные условия введены потому, что они в большей или меньшей степени имеют место на практике.

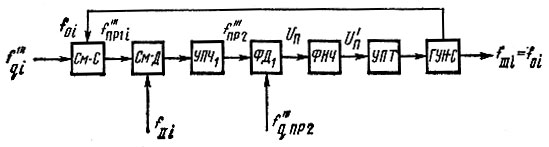
Рис. 4.3. Эквивалентная схема выходной декады активного многодекадного синтезатора СВЧ

На систему подается ряд колебаний с частотами 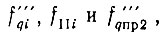нужную степень монохроматичности которых предстоит выяснить. Эти колебания, воздействуя на нелинейные элементы в виде смесителей и фазового дискриминатора, создают на выходах последних биения. Напряжения биений, попадая на управляющий вход ГУН, вызывают паразитные амплитудную и частотную модуляции колебаний последнего.

Если амплитудной модуляцией ГУН при сравнительно малых изменениях управляющего напряжения можно пренебречь, то ЧМ является основной причиной появления побочных составляющих на выходе устройства [143]. Так как индекс этой частотной модуляции ψ_f << 1, степень ослабления побочных составляющих в выходном колебании определяется выражением

где ψ_fП = ΔF_П/F_П - индекс частотной модуляции; ΔF_П - паразитная девиация частоты; F_П - модулирующая частота - в данном случае частота помехи, связанная с частотой побочной составляющей соотношением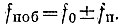

Определим паразитную девиацию частоты на выходе ГУН следующим образом. Как показано в [131], если помеха приложена на выходе фазового дискриминатора, то нормированная предельная частотная характеристика замкнутого кольца ФАПЧ (при υ > 50)

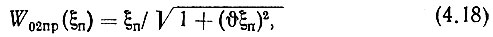
где безразмерная частота помехи ξ_П определяется выражением (2.27). Как правило, 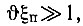поэтому

Паразитная девиация частоты

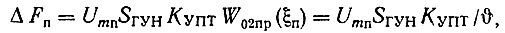
а индекс паразитной ЧМ

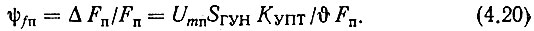
Здесь S_ГУН - крутизна характеристики электрической перестройки ГУН.

Подставляя (4.20) и (4.17) и решая относительно амплитуды напряжения помехи U_mп, получаем

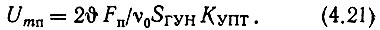
Итак, выражение (4.21) дает амплитуду напряжения помехи на выходе фазового дискриминатора, при которой обеспечивается заданная степень ν₀ подавления побочных составляющих на выходе системы. На входы фазового дискриминатора в стационарном режиме подаются два напряжения U_пр2 и U_qпр2 равных частот f_пр2 = f_qпр2, содержащие в общем случае побочные составляющие. Ограничимся, как и ранее, только одной парой близлежащих побочных составляющих как в том, так и в другом напряжении (рис. 4.4).

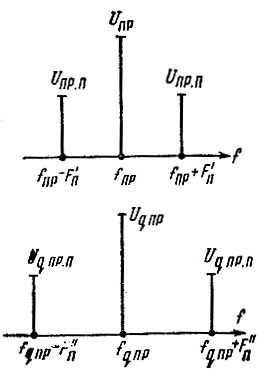
Рис. 4.4. Частотные спектры входных напряжений фазового дискриминатора

Будем рассматривать фазовый дискриминатор как гетеродинный детектор биений. Тогда, учитывая, что u_пр(t) с u_{q пр}(t) дают нулевые биения, возможны ненулевые биения между u_пр(t) и u_{пр п}(t), между u_{q пр}(t) и u_{q пр п}(t) и между u_{пр п}(t) и u_{q пр п}(t) (цифровые индексы у напряжений и частот для общности опущены). Очевидно, что характер первого и второго случаев биений одинаков и вся разница сводится к отличию в индексах. Рассмотрим этот вопрос, воспользовавшись материалами [140] и [147].

Итак, на вход ФД поступает напряжение u_ФДвх(t) = U_{m пр} cos ω_прt + U_{m пр п} cos (ω_пр + Ω'_п)t. Так как в этом напряжении слагаемые имеют разные частоты, то результирующее колебание будет иметь амплитуду U_{m р}(t) и начальную фазу φ_р(t), меняющиеся во времени:

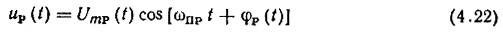
где

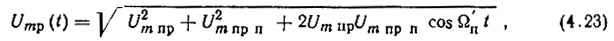
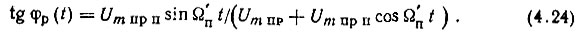
Напряжение на выходе ФД

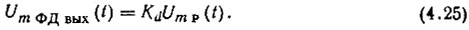
Обычно U_{m пр} >> U_{m пр п}. Поэтому после несложных преобразований выражение (4.25) запишется следующим образом:

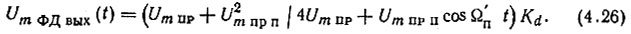
Следовательно, на выходе ФД будет паразитное постоянное смещение, обусловленное негармоничностью подаваемого напряжения ΔE_ФДвых = K_dU²_{m пр п}/4U_{m пр}, и напряжение помехи

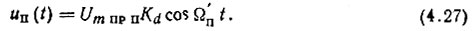
Поскольку K_d ≈ 1, (4.27) примет вид: u_п(t) = U_{m пр п} cos Ω'_пt.

Аналогично можно вывести u_п(t) = U_{mq пр п} cos Ω"_пt.

Таким образом, амплитуда напряжения помехи на выходе ФД оказалась равной амплитуде побочной составляющей на любом его входе:

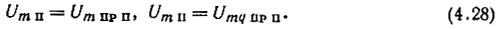
Можно подойти к рассматриваемому вопросу и с несколько других позиций, как это сделано в [148], где исследуется балансный фазовый дискриминатор. На ФД действуют два напряжения, содержащие помехи, причем лучшие результаты фазового детектирования получаются в том случае, когда одно из них вовсе не содержит помех и амплитуда этого напряжения значительно превышает амплитуду другого. Однако если содержание помех в обоих напряжениях примерно одинаково, то оптимальным является равенство напряжений на обоих входах дискриминатора. Для указанных условий и для частного случая Ω'_п = Ω"_п при U_{mq пр} = U_{m пр} >> U_{m пр п} = U_{mq пр п} из выражения (47) работы [148] следует, что U_{m п} = 2 U_{m пр п}.

Таким образом, полученный выше вывод [ф-ла (4.28)] полностью подтверждается [148], ибо ф-ла (47) в этой работе была получена при одновременном действии двух одинаковых по амплитуде и частоте напряжений на входах ФД.

Однако результат биений между U_{q пр п} и U_{пр п} при помощи выражений, полученных в [148], исследовать не удастся. Нельзя также пользоваться выражением (4.26), так как амплитуды U_{mq пр п} и U_{m пр п} могут быть одного порядка. Поэтому необходимо воспользоваться ур-нием (4.23). При U_{mq пр п} = U_{m пр п}

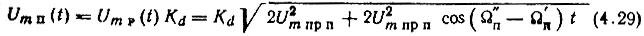
и, если можно положить K_d ≈ 1, то (4.29) запишется в виде

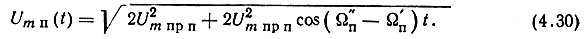
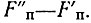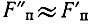Выражение (4.30) показывает, что помеха представляет собой сумму постоянной составляющей и переменного напряжения частоты Если (но не точно равны), то помеха наиболее опасна, ибо имеет самую низкую частоту. Отсюда, в частности, вытекает одно из основных требований к современной системе ДКСЧ: для предотвращения квазинулевых биений все опорные частоты должны находиться в целых кратных отношениях, т. е. формироваться от единственного эталона частоты.

Подводя итоги анализа помехообразования в фазовом дискриминаторе, можно сделать вывод, что требования к амплитудам напряжений помех, поступающих на входы ФД, определяются ф-лой (4.21), а частота помехи для анализа должна выбираться минимальной из всех возможных комбинаций частот поступающих колебаний.

Наиболее сложным вопросом является формулировка требований к входным колебаниям смесителя См-Д, непосредственно предшествующего УПЧ. На этот смеситель поступают два напряжения: "сигнала" - с выхода смесителя См-С (частоты f_{пр1 i}) и гетеродина - от генератора десятков (частоты f_{II i}). Спектры этих напряжений изображены на рис. 4.5. Спектр "сигнального" напряжения состоит из составляющих опорных частот "сотен", смещенных вниз по частоте в смесителе См-С и "загрязненных" побочными составляющими за счет формирования этих частот в МОЧ. Спектр гетеродинного напряжения состоит из "загрязненного" побочными составляющими колебания с выхода генератора десятков за счет неидеальной фильтрации в цепях последнего. Задача сводится к следующему:

- правильному выбору расположения спектров друг относительно друга, т. е. к правильному выбору второй промежуточной частоты;

- расчету необходимого подавления побочных составляющих в спектре "сигнала";

- расчету необходимого подавления побочных составляющих в спектре колебаний гетеродина.

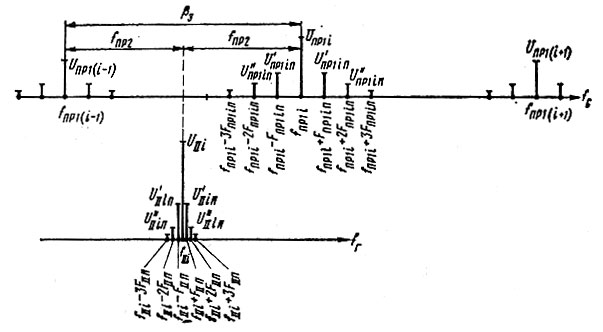
Рис. 4.5. Частотные спектры 'сигнального' и гетеродинного напряжений на втором смесителе декады

Выбор номинального значения второй промежуточной частоты является, как и в технике супергетеродинного приема, компромиссным из-за ряда противоречивых требований. Эти требования общеизвестны, поэтому остановимся лишь на условиях, специфичных для анализируемого устройства.

1. Для получения минимального времени задержки в кольце ФАПЧ полоса пропускания УПЧ (П_УПЧ) должна быть достаточно широкой. Обычно в активных многодекадных синтезаторах СВЧ полосу пропускания УПЧ выбирают не менее

2. Частота любой зеркальной помехи в системе строго фиксирована и определяется механизмом формирования сетки опорных частот.

3. Настройки цепей "сигнала" и гетеродина принципиально не могут быть сопряжены. Поэтому в процессе настройки (автоматической или ручной) гетеродин перестраивается в широкой полосе частот. При этом должна обеспечиваться однозначность настройки*

Учитывая также общую тенденцию построения многоэлементных устройств на транзисторах и интегральных микросхемах, а также применения в УПЧ фильтров сосредоточенной селекции* следует стремиться к уменьшению f_пр2. Так как

вторая промежуточная частота принципиально может быть выбрана как f_пр2 > β₃, так и f_пр2 < β₃. Последнее неравенство может оказаться невыполнимым из-за условия (4.31). Однако, учитывая, реальные значения ΔFД_уд и β₃, а также возможность построения УПЧ с П_УПЧ ≥ 0,4f_пр2, приходим к выводу о выполнимости неравенства f_пр2 < β₃. С другой стороны, выбор f_пр2 > β₃ совершенно не гарантирует от ложной настройки одного из видов:

Правда, выбор f_пр2 < β₃ также не гарантирует от ложной настройки видов

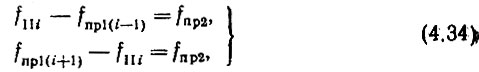
но условия (4.34) имеют одно решение, которое обеспечивает все же правильную настройку.

Естественно, что задача выбора f_пр2 существенно упростилась бы, если напряжения U_пр1(i-1) и U_пр1(i+1) можно было значительно ослабить относительно U_{пр1 i}. Однако это нецелесообразно из-за чрезвычайного усложнения фильтра на выходе генератора гармоник опорных частот 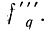С другой стороны, применение специальной схемы для борьбы с зеркальной помехой (например, [П1.3]) значительно усложняет тракт усиления промежуточной частоты.

Итак, предположим, что можно допустить выполнение одного из равенств (4.34) (в данном случае первого) в виде зеркальной помехи. Тогда, очевидно,

Решая совместно (4.32), (4.34) и (4.35), получаем

При таком выборе, однако, амплитуда U_{m пр2} напряжения частоты f_пр2 будет представлять сумму двух несинфазных составляющих, т. е. окажется неустойчивой во времени со всеми вытекающими отсюда условиями приема зеркальной помехи. Во избежание этого необходимо колебание U_пр1(i-1) в какой-то мере ослабить. Если составляющая U_{m пр2}, обусловленная зеркальной помехой, будет иметь порядок 3-5% от полезной составляющей, то работа системы ФАПЧ нисколько не нарушится. Поэтому ослабление U_пр1(i-1) по сравнению с U_{пр1 i} должно быть всего 25-30 дБ.

Необходимо отметить, что ложные настройки могут возникать из-за принципиально присущего супергетеродинному методу получения промежуточной частоты на гармониках сигнала и частоты гетеродина, а также из-за получения промежуточной частоты при умножении в смесителе субгармоники f_пр2 (так называемая "полузеркальная помеха" [130]).

Анализу режимов смесителей с целью получения существенного превышения напряжения промежуточной частоты от основного преобразования (первые гармоники сигнала и гетеродина) над напряжениями высших комбинационных частот посвящено большое число работ. Наиболее конкретная рекомендация на этот счет содержится в статье [149] и заключается в том, что для выполнения сформулированного требования необходимо значительное (порядка 15 дБ и более) превышение уровня колебаний гетеродина над уровнем сигнала или оптимизация режима смесителя по постоянному току. Заметим, что к такому же решению приходит автор патента [П2.48], который рекомендует создать это превышение не менее 20 дБ.

Кроме указанных, можно привести еще и следующие рекомендации, также способствующие успешной борьбе с ложными настройками: правильный выбор коэффициентов ручной (РРУ) и автоматической (АРУ) регулировки усиления УПЧ, применение балансных смесителей [130], выбор частот гетеродинирующих напряжений и "сигналов" так, чтобы первые превышали вторые, особенно в первом смесителе декады, где f_{пр i} велики [150], т. е.

и т. д. в других декадах.

Рассмотрим теперь необходимое подавление побочных составляющих в спектрах "сигнала" и напряжения гетеродина. При этом, в отличие от предыдущего анализа, будем интересоваться не низкочастотными составляющими, а такими, которые близки к промежуточной частоте. Выбор f_пр2 в соответствии с выражением (4.36) и ослабление U_пр1(i-1) ≅ (0,03÷0,05) U_{пр1 i} дает основание не считаться с побочными составляющими, отстоящими на ±β₃.

Однако прежде чем продолжить анализ, вернемся к выражению (4.21) и преобразуем его таким образом, чтобы прийти к отношению максимального полезного напряжения на выходе фазового дискриминатора Е_уд к амплитуде напряжения помехи U_mп. Как очевидно,

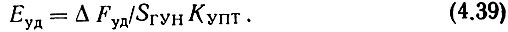
Решая совместно (4.21) и (4.39), получаем

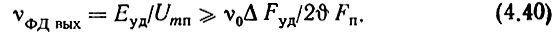
Воспользуемся снова выводами работы [148], из которой следует, что при ρ₁ = ρ₂ = ρ и равенстве амплитуд напряжений, подаваемых на входы фазового дискриминатора,

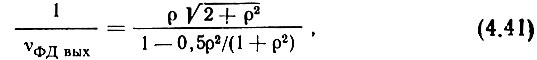
где

Попытка решения (4.41), как 1/ρ = f(1/ν_ФДвых), приводит к уравнению шестой степени

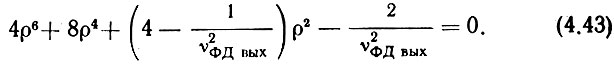
Упростить столь сложную задачу можно, вспомнив, что ρ << 1. Поэтому, пренебрегая малыми величинами 0,5ρ⁶ и ρ⁴, получим

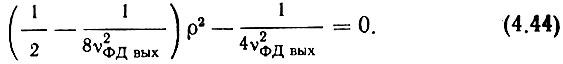
Решением ур-ния (4.44) с учетом того, что 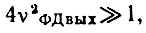будет выражение

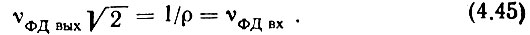
Вернемся теперь к вопросу подавления побочных составляющих в "сигнальном" U_{пр1 i} и гетеродинном U_{II i} напряжениях, действующих на смеситель См-Д. При этом будем полагать смеситель линейным, безынерционным. Заметим, что подобная задача в несколько ином плане решалась в [151]. Вначале будем считать оба напряжения строго гармоническими: 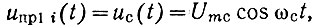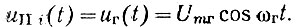В реальных случаях

и

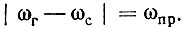
Так как ω_с ≠ ω_г, то амплитуда результирующего напряжения найдется как векторная сумма, модуль которой

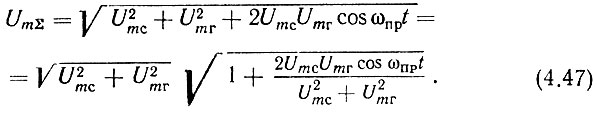
Учитывая неравенство (4.46), упростим (4.47):

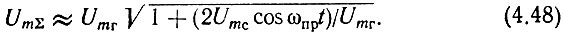
Так как второе слагаемое под радикалом (4.48) значительно меньше единицы, его можно разложить в биномиальный ряд и ограничиться пятью членами ряда. Опуская несложные алгебраические и тригонометрические преобразования, запишем окончательно

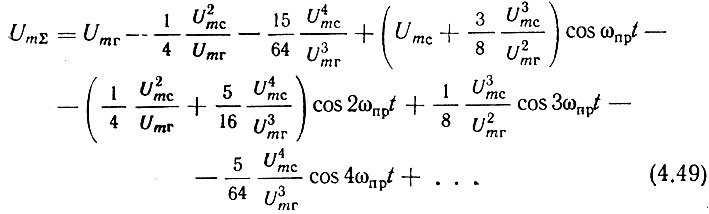
В данном анализе интерес представляют только колебания, проходящие через УПЧ. Очевидно, что они отражаются четвертым слагаемым выражения (4.49):

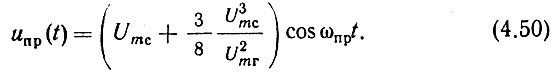
Здесь могут встретиться два случая:

- напряжения "сигнала" и гетеродина амплитудномодулированы;

- напряжение "сигнала" модулировано по амплитуде, а гетеродина - по частоте.

Рассмотрим первый случай:

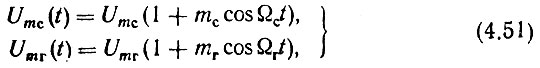
где, применительно к рассматриваемой схеме,

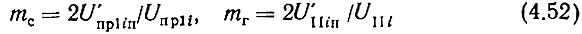
и

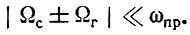
Подставим (4.51) в (4.50):

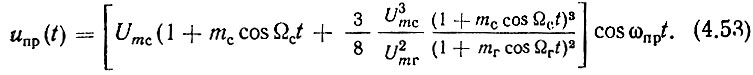
Так как m_с << 1 и m_г << 1, можно пренебречь членами, содержащими квадраты этих коэффициентов. Выполнив преобразования, получим окончательно

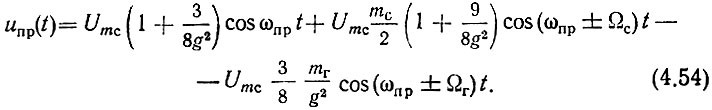
Выражение (4.54) содержит основные компоненты преобразования, попадающие в полосу пропускания УПЧ: напряжение промежуточной частоты U_пр (первый член), помеху U_пс, обусловленную негармоничностью напряжения "сигнала" (второй член) и помеху U_пг, обусловленную негармоничностью напряжения гетеродина (третий член). Из (4.54) учитывая, что m_c = 2/ν_{См вх}, m_г = 2/ν_{II i} и (4.46), получаем

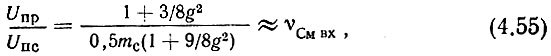
а также

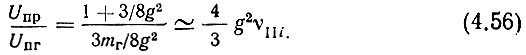
Из (4.55) и (4.56), в частности, вытекает, что если спектр АМ - сигнала не шире полосы пропускания УПЧ, то при линейности и безынерционности смесителя продукты преобразования не зависят от отношения напряжения гетеродина к напряжению "сигнала" и, наоборот, коэффициент преобразования спектральных составляющих напряжения гетеродина в значительной мере определяется этим отношением.

Очевидно, что должны удовлетворяться следующие равенства:

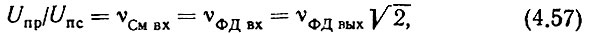
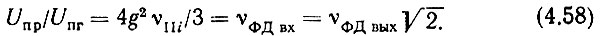
Обычно все измерения в диапазонах ДМВ и СМВ производятся применительно к мощностям. Так как рассматриваемые попарно напряжения действуют на общих сопротивлениях, для перехода к отношению мощностей отношения напряжений возводят в квадрат, т. е.

Решая совместно (4.57), (4.40) и учитывая (4.59), получаем

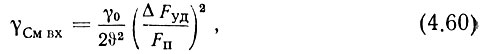
где

Решая совместно (4.58), (4.40) и учитывая (4.59) и (4.61), получаем

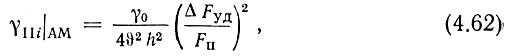
где

Если при конкретных расчетах выражения (4.60) и (4.63) не дают значений γ_{См вх} >> 1 и γ_{II i} >> 1, то их следует принимать таковыми из условия удобства настройки ГУН.

Рассмотрим теперь случай, когда напряжение "сигнала" модулировано по амплитуде, а напряжение гетеродина - по частоте. Обычно Ω_c ≠ Ω_г. Поэтому можно рассматривать воздействие побочных составляющих в напряжениях "сигнала" и гетеродина на напряжение промежуточной частоты взаимонезависимо. Результат воздействия АМ "сигнала" на систему был выяснен выше [частный случай, когда в (4.51) m_г = 0] и нашел отражение в ф-ле (4.60).

Выясним воздействие на систему частотной модуляции гетеродина. Если частота модуляции меняется во времени f_II(t) = f_{II 0} + Δf_II(t), то, учитывая, что f_пр2(t) = |f_пр1-f_II(t)|, получим f_пр(t) = f_пр20 + Δf_II(t), или, другими словами, ЧМ гетеродина полностью передается через смеситель на колебание промежуточной частоты. Таким образом, если u_II(t) = U_mII cos(ω_IIt + ψ_fsin Ω_IIt), то u_пр2(t) = U_{m пр2}cos(ω_пр2t + ψ_fsin Ω_IIt).

Последнее дает право записать, что при разомкнутом кольце ФАПЧ

Для определения зависимости между коэффициентами гармоничности выходных колебаний последней и предпоследней декад необходимо учесть нормированную частотную характеристику кольца ФАПЧ, отражающую прохождение помех на выход системы при частотной модуляции опорной частоты W₀₁(ξ_п) [131]. При υ > 50 можно учитывать предельное значение этой характеристики

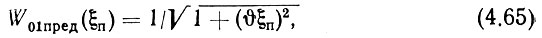
где

Как указывалось выше, обычно 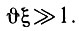Поэтому (4.65) с учетом (4.66) можно записать в виде

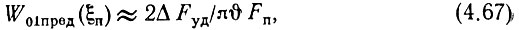
а равенство (4.64) для замкнутого кольца ФАПЧ - в виде

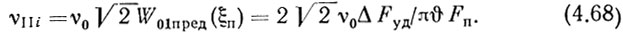
С учетом (4.59) и (4.61) выражение (4.68) окончательно запишется как

Важным достоинством применения ФАПЧ является весьма значительная зависимость ослабления побочных составляющих от частоты помехи. Действительно, во все выражения, связанные с коэффициентами гармоничности колебаний, частота помехи входит в знаменатель множителем во второй степени. Отсюда следует практический вывод о возможности полного пренебрежения всеми побочными составляющими, кроме одной, ближайшей по частоте к основному колебанию.

Заметим, наконец, что если смеситель выполнить по отношению к сигналу линейным не удастся и он окажется квадратичным, продукты модуляции напряжения гетеродина в смесителе подавляться не будут (аналогичный пример, касающийся двух АМ колебаний, приведен в [151]), В этом случае γ_{II i}|AM, очевидно, следует рассчитывать по ф-ле (4.60), т. е. так же, как и γ_{См вх}. То же самое произойдет, если линейный смеситель не удастся выполнить безынерционным.

Как видно из рис. 4.5, паразитное напряжение промежуточной частоты может образоваться на выходе смесителя не только из-за действия зеркальной помехи, но и под влиянием следующих двух факторов: в результате биений между составляющими сетки "сигнала", отстоящими друг от друга на f_пр2; появления в результате биений между отдельными составляющими сетки "сигнала" частоты, в целое число раз меньшей f_пр2, и затем умножения этой частоты на нелинейности смесителя до f_пр2. Несмотря на незначительность этого эффекта, его следует оценить, в особенности для первого случая. Это можно сделать, в частности, для одной из составляющих, если в выражении (4.53) не пренебрегать членом с m²_с и положить Ω_c = ω_пр. В этом случае напряжение паразитной промежуточной частоты

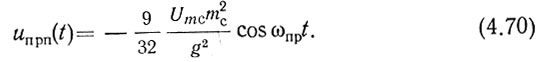
Отношение

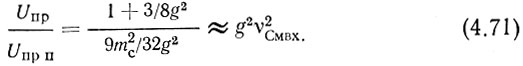
Если для нормальной работы системы потребовать U_пр/U_{пр п} = 100 и учесть, что подобных комбинаций в реальной системе может быть примерно в 8-10, также что эти составляющие должны из-за несинфазности складываться квадратично, то можно получить

При достаточно больших h величина γ_{См вх}, полученная из (4.72), оказывается значительно меньше этой же величины полученной из (4.60).

Этим, в первом приближении, и исчерпывается анализ воздействия побочных составляющих на активный многодекадный синтезатор с использованием аналоговой ФАПЧ. Действительно, во-первых, к "сигналам", поступающим на смеситель См-С (см. рис. 4.3), требования уже были предъявлены, ибо они ничем не отличаются от требований к напряжению "сигнала", поступающего на смеситель См-Д. Во-вторых, требования к колебаниям с выхода декады десятков также были сформулированы при выводе выражения (4.69). В-третьих, требования к выходным колебаниям декады единиц отражаются ф-лой (4.62), если декада является пассивной ЯФУ, и (4.69), если она построена на базе кольца ФАПЧ. Требования же к напряжению опорной частоты, поступающему на фазовый дискриминатор декады десятков, ничем не отличаются от сформулированных выше требований к такому же напряжению, поступающему на фазовый дискриминатор выходной декады.

Однако здесь пока еще не был освещен весьма важный частный случай, когда побочные составляющие в колебаниях гетеродина второго смесителя декады либо при преобразовании, либо непосредственно на выходе последнего дают колебания, попадающие в полосу пропускания второго УПЧ. Очевидно это происходит, во-первых, если частота побочной составляющей отстоит от частоты гетеродина на

т. е. частота побочной составляющей равна 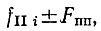либо если частота побочной составляющей непосредственно равна F_пп. В обоих случаях, даже если "сигнал" на второй смеситель декады не подается, на выходе УПЧ появляется напряжение промежуточной частоты. Назовем для краткости такие помехи "полосными".

Вполне очевидно, что с точки зрения получения заданного коэффициента гармоничности колебаний на выходе системы "полосные" и остальные побочные составляющие ничем друг от друга не отличаются - необходимая степень их подавления на входе кольца ФАПЧ определяется выражением (4.60) или (4.62), либо (4.69). Особенность требований к коэффициенту гармоничности гетеродинного колебания по "полосным" помехам состоит в том, что паразитное напряжение на выходе второго УПЧ декады, обязанное своим происхождением "полосным" помехам, не должно нарушать нормальной работы кольца ФАПЧ. Выше отмечалось, что это требование выполняется, если амплитуда паразитного напряжения не превосходит 3-5% амплитуды основного напряжения промежуточной частоты.

Считая коэффициент передачи второго смесителя декады по обоим входам одинаковым, запишем отмеченное условие следующим образом:

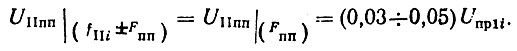
Коэффициент гармоничности гетеродинного напряжения по частотам помехи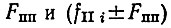

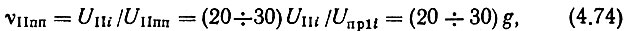
где g определяется равенством (4.56).

С учетом (4.63) выражение (4.74) запишется в виде

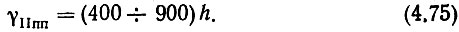
Таким образом, чтобы облегчить условия фильтрации колебаний гетеродина, желательно увеличивать напряжение (мощность) "сигнала", оставляя во избежание ложной настройки h ≥ 15 дБ. С этой целью в декаде между первым и вторым смесителями целесообразно включить УПЧ₁.

Следует отметить, что если в качестве гетеродина применить пассивную ЯФУ (пассивный фильтр с усилителем), то "полосные" побочные составляющие необходимо учитывать в полной мере. Если же в качестве гетеродина используется активная ЯФУ с ФАПЧ, то так как f'''_пр2 = 0,5β₃ = 5β₂ = 10f"_пр2, "полосная" помеха через УПЧ₂ ячейки с ФАПЧ практически не пройдет и в этом случае с "полосными" побочными составляющими можно не считаться.

Таким образом, в схеме рис. 2.7 в декаде сотен можно иметь один УПЧ, но в декаде десятков - обязательно два, а коэффициенты гармоничности колебаний декады единиц рассчитывать, пользуясь выражениями (4.62), (4.73) и (4.75). Благодаря тому, что в декаде десятков применено кольцо ФАПЧ, коэффициент гармоничности выходных колебаний этой декады можно рассчитывать, пользуясь только выражением (4.69).