
4.3. Требования к подавлению побочных составляющих в колебаниях опорных частот цифровых синтезаторов
Рассмотрим эквивалентную схему цифрового синтезатора СВЧ, соответствующего структурной схеме рис. 3.1б (рис. 4.6). Как видно из сравнения этих рисунков, они отличаются тем, что в схеме рис. 4.6 комбинация ДФКД-ДПКД заменена одним делителем промежуточной частоты ДПЧ с коэффициентом деления, равным произведению cυ, а также наличием индекса i и шага дискретности β1 у опорной частоты 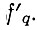 Необходимость последнего нововведения будет понята из дальнейшего.
Необходимость последнего нововведения будет понята из дальнейшего.
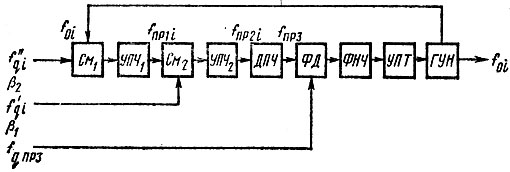
Рис. 4.6. Эквивалентная схема цифрового синтезатора СВЧ
Для анализа эквивалентной схемы цифрового синтезатора (рис, 4.6) ее целесообразно сравнить с эквивалентной схемой выходной декады активного многодекадного синтезатора (см. рис. 4.3). Из сравнения вытекает, во-первых, появление нового элемента ДПЧ, включенного между усилителем второй промежуточной частоты и фазовым дискриминатором, и, во-вторых, смена индексации опорных частот (включение УПЧ между первым и вторым смесителями не является различием, так как он может присутствовать и в декаде аналоговой ФАПЧ, что следует из предыдущего параграфа, а также может отсутствовать в цифровом синтезаторе при невозможности его практического выполнения).
Вместо колебаний опорных частот 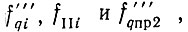 подаваемых на устройство рис. 4.3, на систему рис. 4.6 подаются соответственно колебания опорных частот
подаваемых на устройство рис. 4.3, на систему рис. 4.6 подаются соответственно колебания опорных частот 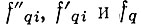 пр3, нужную степень монохроматичности которых здесь и предстоит выяснить.
пр3, нужную степень монохроматичности которых здесь и предстоит выяснить.
По-прежнему предположим, что УПЧ достаточно широкополосны, линейны и безынерционны, ФНЧ - пропорционально-интегрирующий с отношением постоянных времени υ > 50, УПТ - широкополосный, безынерционный, с коэффициентом передачи по постоянному току КУПТ. Как и ранее, пренебрежем паразитной амплитудной модуляцией ГУН под воздействием помех, а причиной появления побочных составляющих будем считать его паразитную частотную модуляцию. Так как индекс этой ЧМ ψf << 1, то для коэффициентов гармоничности выходных колебаний ГУН справедливо соотношение (4.17).
Необходимый коэффициент гармоничности в опорном колебании ФД (частота fq пр3) можно было бы найти так же, как и в предыдущем параграфе, принимая во внимание, что частотная характеристика кольца ЦФАПЧ для этого источника помех определяется произведением коэффициентов передачи пропорционально-интегрирующего ФНЧ и ФД типа "выборка - запоминание" [ф-ла (3.28)] с учетом неидеальности этого ФД. Однако практическая ценность такого анализа мала. Действительно, в реальной системе ДКСЧ СВЧ диапазона частота fq пр3 является минимальной частотой, формируемой из эталонной частоты fq0 путем деления. Следовательно, побочные составляющие могут быть только гармониками частоты fq пр3, а как было выяснено в § 3.2, при достаточном подавлении помехи частоты Fп = fqФД помехи кратных частот практически могут не учитываться.
Следующей особенностью цифрового синтезатора по сравнению с выходной декадой многодекадного синтезатора является изменяющееся значение второй промежуточной частоты fпр2 i (напомним, что в активном многодекадном синтезаторе fпр2 = fq пр2 = const). Поэтому при тех же общих рекомендациях выбор номинальных значений fпр2 i будет иным. Действительно, полоса пропускания УПЧ1 должна быть

При одной неизменной частоте f'q полоса пропускания УПЧ2 также должна быть не менее β2, т. е. реально fпр2 макс > β2. Отсюда следует, что максимальное быстродействие ДПЧ fДПЧ макс = fпр2 макс > β2.
Однако на практике быстродействие интегральных микросхем, на базе которых строятся ДПЧ, оказывается, как правило, ниже шага дискретности опорных частот β2. Поэтому целесообразно иметь две опорных частоты f'q, переключающихся с шагом дискретности:

При этом
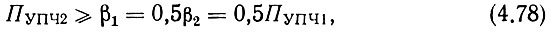
т. е. можно осуществить равенство fДПЧ макс = fпр2 макс < β2, что позволит легче отказаться от применения ДФКД в ДПЧ и тем самым улучшить характеристики синтезатора.
В § 4.2 был сделан вывод о том, что для предотвращения вредного влияния нерабочих составляющих сетки опорных частот f"q на работу кольца они должны подавляться на 25-30 дБ полосовым фильтром, включенным между генератором гармоник и первым смесителем. Кроме того, во избежание ложных настроек рекомендовалось обеспечить превышение мощности гетеродина над мощностью "сигнала" на входах смесителя не менее 15 дБ, применять балансные смесители и т. д. Все эти рекомендации справедливы и для цифрового синтезатора СВЧ.
Необходимо иметь в виду также следующее. Введение в кольца ФАПЧ делителя частоты уменьшает коэффициент передачи разомкнутого кольца в cυ раз. Как будет показано в следующей главе, при этом во столько же раз уменьшается компенсация кольцом собственных флуктуаций частоты (фазы) ГУН. С другой стороны, с ростом частоты ГУН увеличивается интенсивность этих флуктуаций (в частности, шумов). Следовательно, с увеличением f0 необходимо увеличивать коэффициент передачи кольца. Для этого целесообразно так взаимно расположить частоты в системе, чтобы с ростом f0 коэффициент деления ДПКД уменьшался. Последнее, в свою очередь, возможно при следующих двух комбинациях:
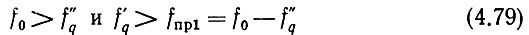
или
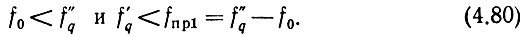
Следует заметить, что выполнение неравенств (4.79) и (4.80) не обеспечивает, особенно при меняющейся частоте f'q, полной компенсации, однако облегчает ее получение.
Рассмотрим вопрос о необходимом подавлении побочных составляющих в колебаниях опорных частот f"q и f'q. При этом, как и ранее, имея в виду линейность характеристик первого смесителя и УПЧ1, будем считать, что побочные составляющие в колебаниях частот f"q действуют на сигнальном входе второго смесителя, а колебание частоты f'qi является гетеродинным.
В такой постановке задача уже решалась в предыдущем параграфе. При этом колебание, содержащее побочные составляющие" представлялось в виде АМ сигнала, если оно поступало с выхода пассивной ЯФУ (пассивный фильтр с усилителем или без него) и в виде ЧМ сигнала, если оно поступило с выхода кольца ФАПЧ. Так как к коэффициентам гармоничности колебаний опорных частот устройства рис. 4.6 не предъявляются жесткие требования, эти колебания формируются пассивными ЯФУ. Поэтому будет справедливым при анализе представлять их в виде АМ сигналов.
Для указанных условий были получены выражения (4.55) и (4.56), которые при линейности и безынерционности второго смесителя кольца связывают коэффициенты гармоничности напряжений на выходе УПЧ2 и на обоих выходах второго смесителя. Эти выражения пригодны и при анализе цифрового синтезатора. Для ясности заменим индексы: в (4.55) вместо νСм вх запишем ν"q, а в (4.56) вместо νII i - ν'q.
Прежде чем продолжить анализ, необходимо отметить две особенности прохождения помех по кольцу ЦФАПЧ. Во-первых, между УПЧ2 и фазовым дискриминатором включен делитель частоты. В § 4.1 указывалось, что при умножении частоты колебания, содержащего побочные составляющие, даже если оно представлено АМ сигналом, коэффициент гармоничности напряжения уменьшается в определенное число раз, равное коэффициенту умножения, а при делении частоты - увеличивается в число раз, равное коэффициенту деления.
На первый взгляд, с учетом применения в ДПЧ триггерных делителей частоты, это утверждение может показаться странным. Действительно, если бы из синусоидальных колебаний на входе ДПЧ формировались идеальные прямоугольные импульсы (фронт и спад соответствуют прохождению синусоиды через нулевое значение), то далее триггерными делителями частоты осуществлялась бы полная демодуляция АМ колебания (коэффициент гармоничности увеличивался бы до бесконечности). Однако фактически входной каскад ДПЧ (из-за высокой входной частоты) формирует импульсы, по форме весьма далекие от прямоугольных (трапецеидальные, близкие к треугольным). Если же такая последовательность модулирована по амплитуде, то на первом же пороговом устройстве она оказывается промодулированной по фазе (часто те), ну а далее в процессе деления частоты индекс модуляции уменьшается в число раз, равное коэффициенту деления и во столько же раз возрастает коэффициент гармоничности напряжения. Насколько близко преобразование АМ в ФМ к линейному в общем виде определить невозможно - это зависит от конкретных схем формирователей импульсов и делителей. Однако для расчета его можно принять таковым, не совершив при этом серьезной ошибки.
Во-вторых, хотя, как следует из выражения (3.28), периодически-максимальные значения коэффициента передачи идеального фазового дискриминатора типа "выборка - запоминание" с ростом частоты уменьшаются, из-за проходных паразитных емкостей ключей этого ФД коэффициент передачи высокочастотных помех реальным фазовым дискриминатором может не уменьшаться, а, наоборот, расти. Так как реальность характеристики ФД можно выяснить только экспериментально, примем пока с запасом коэффициент передачи ФД для помех равным единице.
С учетом сделанных замечаний на основании выражений (4.55) и (4.56) можно записать:
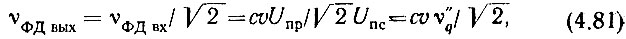
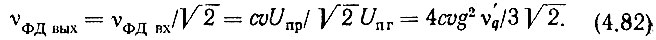
Если продолжить анализ, как это было сделано в § 4.2, то можно прийти к выражениям (4.60) и (4.62), в которых знаменатель правой части будет содержать произведение (cυ)2. Однако следует помнить, что если относительно коэффициентов гармоничности колебаний опорных частот f'q и f"q изложенное является абсолютно справедливым, то распространять это на коэффициент гармоничности опорного колебания fq пр2 будет грубой ошибкой". Математически это будет показано в следующей главе. Работа кольца ФАПЧ основана на том, что любому изменению фазы на входе ФД соответствует такое изменение частоты ГУН, которое: компенсирует указанное изменение фазы с остаточной ошибкой, обратно пропорциональной коэффициенту передачи кольца. Последнее же означает, что изменение частоты ГУН должно быть, равно отклонению опорной частоты, если источник последней включен между ГУН и ДПЧ, и должно быть в cυ раз больше, если, источник включен в кольцо после ДПЧ.
Таким образом, в случае цифрового синтезатора получаются, выражения, аналогичные (4.60) и (4.62):

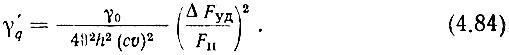
Здесь нужно отметить следующее. Во-первых, если выражения (4.83) и (4.84) при конкретных расчетах не дают значений 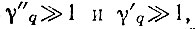 то их следует принимать таковыми из условий удобства настройки ГУН. Во-вторых, если смеситель выполнить линейным и безынерционным не удается, то выражение (4.84) окажется несправедливым. В этом случае для определения γ'q необходимо пользоваться ф-лой (4.83). В-третьих, для учета биений между составляющими сетки частот, отстоящими друг от друга на вторую промежуточную частоту, можно пользоваться выражением (4.72).
то их следует принимать таковыми из условий удобства настройки ГУН. Во-вторых, если смеситель выполнить линейным и безынерционным не удается, то выражение (4.84) окажется несправедливым. В этом случае для определения γ'q необходимо пользоваться ф-лой (4.83). В-третьих, для учета биений между составляющими сетки частот, отстоящими друг от друга на вторую промежуточную частоту, можно пользоваться выражением (4.72).
Рассматривая вопрос о "полосных" побочных составляющих в цифровом синтезаторе, следует указать на полную идентичность требований по их подавлению с требованиями в активном многодекадном синтезаторе:

при этом
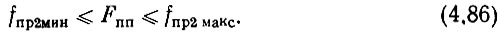
Заметим, что комментарии к выражению (4.75) остаются справедливыми и применительно к ф-ле (4.85). Таким образом, в цифровом синтезаторе СВЧ включение УПЧ1 следует считать правилом.
Обратимся теперь к случаю двухкольцевого цифрового синтезатора СВЧ, структурная схема которого изображена на рис. 3.5. Как нетрудно видеть, выходное кольцо этого синтезатора (с аналоговой ФАПЧ) по построению ничем не отличается от выходной декады активного многодекадного синтезатора рис. 2.7. Поэтому для анализа побочных составляющих в колебаниях опорных частот этого кольца целиком применимы выражения и выводы § 4.2.
Вторая часть цифрового синтезатора рис. 3.5 построена на базе кольца ЦФАПЧ с одним преобразованием опорной частоты f'q, где гетеродином для смесителя служит ГУН. Поэтому весь расчет сведется к определению необходимых значений коэффициентов гармоничности колебаний опорной частоты f'q с использованием (4.83).

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
