4.4. Анализ шумовых характеристик многодекадных синтезаторов

Важнейшим параметром системы ДКСЧ наряду с коэффициентами гармоничности колебаний является ее шумовая характеристика. Если представить все устройство ДКСЧ в виде эквивалентного генератора, то его выходные колебания оказываются промодулированными шумом как по амплитуде, так и по углу (по фазе и по частоте). Как уже упоминалось, основным источником шума в СВЧ системах ДКСЧ, определяющим шумовые характеристики выходных колебаний последней, является опорный кварцевый (квантовый) генератор эталона частоты. Уровень же частотных и фазовых составляющих шумов кварцевого генератора обычно значительно (не менее чем на 10-20 дБ [152]) превышает уровень его АМ шумов (в молекулярных и атомных эталонах частоты наблюдаются те же явления). Поэтому при анализе шумовых характеристик систем ДКСЧ СВЧ диапазона будем учитывать лишь их частотные (фазовые) шумы.

Правильность такого решения подтверждается также и тем, что радиосистемы, в состав которых входят устройства ДКСЧ СВЧ диапазона, критичные по воздействию на них шумов возбудителей передатчиков и гетеродинов приемников (устройств ДКСЧ), обычно используют ЧМ и ФМ. Наиболее чувствительны к воздействию указанных шумов многоканальные линии связи СВЧ диапазона. Поэтому целесообразно анализ провести применительно к этому случаю, а точнее, считать систему ДКСЧ гетеродином приемника многоканальной радиолинии с ЧМ (ФМ).

Шумовые характеристики системы ДКСЧ могут задаваться либо в виде отношения мощности несущей к мощности шума, измеренной в заданной полосе частот, либо в виде шумовой девиации частоты или фазы (среднеквадратичного значения), также измеренной в заданной полосе частот, либо, наконец, в виде относительной кратковременной нестабильности частоты, измеренной за заданное время усреднения.

Для радиолинии обычно задается отношение сигнал/шум в канале связи (с/ш) за счет гетеродина (возбудителя)

где Р_ш - мощность шума в канале связи, обязанная своим происхождением шумам гетеродина (возбудителя), мощность которых на выходе гетеродина (возбудителя) обозначим через Р_ш0.

На выходе гетеродина (возбудителя) отношение несущая/шум (н/ш)

Как показано в [153], при частотной модуляции η₀ ≠ η_к. При этом под η₀ понимают отношение н/ш на входе приемника, а под η_к - отношение с/ш в канале связи. Так как выше было принято, что интерес представляет отношение η_к только за счет гетеродина, то выводы работы [153] относительно η₀ справедливы лишь применительно к выходу гетеродина. Так, при частотной модуляции

где ψ_сf - индекс ЧМ сигнала в канале связи.

Кроме того, в [153] показано, что в качестве шумовой полосы нужно принимать не полосу пропускания УПЧ, а П_ш = 2F_{м макс}, где F_{м макс} максимальная модулирующая частота передаваемого сообщения.

Часто для гетеродина радиолинии задается максимально допустимая шумовая девиация частоты σ_кf в канале (так как шумы являются случайным процессом, здесь и ниже можно говорить только о среднеквадратичном значении девиации частоты как о квадратном корне из дисперсии частных шумов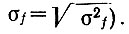

Имея в виду, что η₀ >> 1, определим шумовую девиацию на выходе системы ДКСЧ при различных способах задания шумовых характеристик. Предварительно напомним, что если задана шумовая девиация частоты σ_0f, измеренная в полосе частот, ограниченной 0-F_{м макс}, то дисперсия частотных флуктуаций σ²_0f есть средняя мощность шума в полосе 0-F_{м макс}, численно равная автокорреляционной функции от нулевого аргумента. Действительно, как известно, автокорреляционная функция от τ

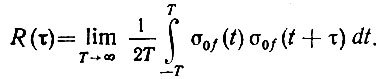
При τ = 0 это выражение принимает вид

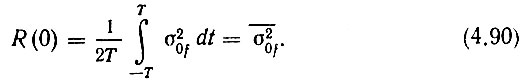
Но, с другой стороны, энергетический спектр

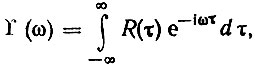
, а

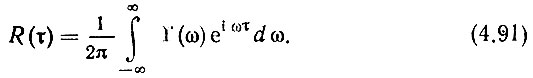
При τ = 0 (непрерывный спектр), имея в виду, что спектр задается в интервале частот 0-Ω_{м макс}, из (4.90) и (4.91) получаем

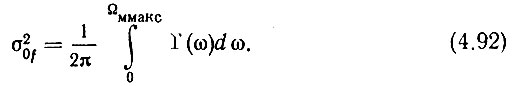
Из Приложения 1 к работе [154] известно, что при равномерном спектре шумового воздействия и узкополосной ЧМ энергетический спектр выражается как

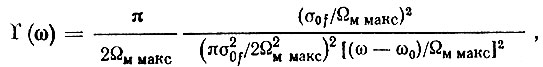
т. е. частотное распределение энергетического спектра есть относительно сложная функция от σ_0f и Ω_{м макс}. Так как реально шумовое воздействие (модулирующее напряжение шума) не является спектрально равномерным, то энергетический спектр оказывается еще более сложной и заранее неопределенной функцией. С другой стороны, для анализа и расчета, в первую очередь, необходимо знать не столько точное частотное распределение энергетического спектра, сколько площадь, заключенную под огибающей этого распределения (σ²_0f). Поэтому можно предположить, что энергетический спектр постоянен и равен 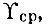т. е. ординате прямоугольника, которая, будучи умноженной на Ω_{м макс}, дает площадь равновеликую, ограниченную осями координат и кривой частотного распределения энергетического спектра.

Подставляя 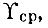в (4.92), получаем 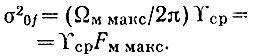Так как по определению энергетический спектр есть в определенном масштабе мощность шума, заключенная в полосе 1 Гц, то последнее выражение подтверждает, что дисперсия σ²_0f представляет собой в том же масштабе мощность шума в полосе 0-F_{м макс}.

Таким образом, если задано отношение н/ш на выходе системы ДКСЧ η₀ в полосе модулирующих частот 0-F_{м макс}, то

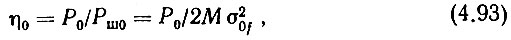
где М - постоянный коэффициент, имеющий размерность [В²/Ом Гц²] = [Вт/Гц²].

Из выражения (4.93) имеем

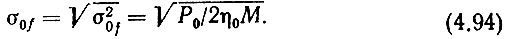
При заданном отношении с/ш в канале связи η_к родина из (4.89) находим за счет гетеродина из (4.89) находим

Но

где ΔF_с - полезная девиация частоты в канале связи.

Подставляя (4.93) и (4.96) в (4.95), получаем

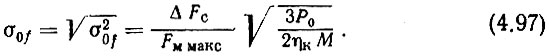
Если, наконец, задается шумовая девиация частоты в канале связи за счет гетеродина σ_кf, то, имея в виду, что η_к = ψ²_сf/ψ²_кшf = ψ²_cfF²_{м макс}/σ²_кf, подставим это выражение и (4.93) в (4.89):

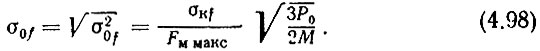
Для расчета шумовых характеристик системы ДКСЧ вначале проанализируем шумовые характеристики активного многодекадного синтезатора с аналоговой ФАПЧ, для чего рассмотрим эквивалентную схему его выходной декады (рис. 4.7а). Как указывалось выше, полоса пропускания кольца ФАПЧ выбирается такой, чтобы шумы на выходе системы определялись шумами колебаний опорных частот. Однако даже если предположить, что шумы в опорных колебаниях отсутствуют, а собственные шумы ГУН полностью компенсируются, то за счет элементов, входящих в кольцо ФАПЧ (смесителей, УПЧ и т. п.), на выходе фазового дискриминатора появится напряжение шумов, которое, воздействуя на ГУН, приведет к шумовой девиации частоты последнего. Поэтому шумы элементов кольца необходимо учитывать.

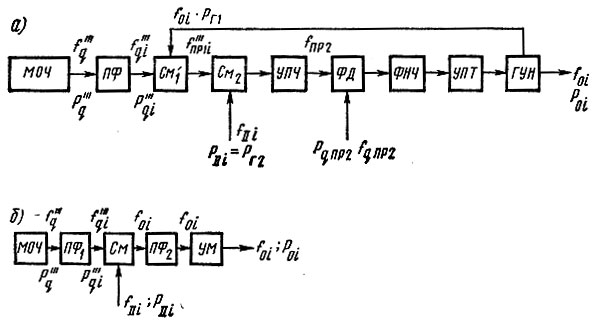
Рис. 4.7. Эквивалентные схемы для расчета шумовых характеристик выходной декады многодекадного синтезатора СВЧ: а) активного; б) пассивного

Так как заданной оказывается величина σ_0f на выходе системы, то, очевидно, требуется так рассчитать последнюю, чтобы ее коэффициент шума и отношение н/ш входных колебаний опорных частот обеспечивали выполнение этого требования. Сначала считаем кольцо ФАПЧ разомкнутым. Как видно из рис. 4.7а, в системе имеются два нелинейных элемента: фазовый дискриминатор ФД и ГУН (смесители, как известно, могут считаться линейными устройствами при значительном превышении мощности гетеродина над мощностью сигнала и при достаточно большой мощности гетеродина).

Прежде чем составить общее уравнение системы с точки зрения ее шумовых характеристик, целесообразно выяснить шумовые характеристики фазового дискриминатора. Задача может быть сформулирована следующим образом. На вход ФД подается напряжение опорной частоты в определенном отношении с шумом. Требуется определить отношение н/ш на выходе ФД с учетом собственных шумов последнего и шумовых характеристик напряжения опорной частоты.

Воспользуемся некоторыми данными, приводимыми в литературе, которые позволят ответить на поставленный вопрос. В [155] отмечается, что система ФАПЧ работает еще нормально при отношении н/ш на входе ФД, не меньшем трех, а в работе [156], - что при отношении н/ш более пяти характеристика ФД может считаться линейной; в [157] делается вывод о том, что линейный фазовый дискриминатор не изменяет отношения н/ш.

Поскольку в реальных системах отношение н/ш на входе ФД всегда больше пяти, будем считать фазовый дискриминатор линейным элементом, а его собственные шумы и шумы напряжения опорной частоты f_пр2 будем учитывать так же, как собственные шумы смесителей и шумы подаваемых на них гетеродинирующих колебаний.

Таким образом, начиная с выхода МОЧ и кончая входом ГУН, систему относительно "сигнала" и шумов можно считать линейной. Поэтому, если известно отношение η₀ или σ_0f, крутизна электрической настройки ГУН S_ГУН и входное сопротивление цепи управления последнего R_{вх г}, то можно определить допустимый коэффициент шума линейной части системы N_шл, который и обеспечит получение заданного отношения η₀.

Заметим, что, как было доказано выше, амплитудную модуляцию ГУН, в том числе и шумами, можно не учитывать. Поэтому будем рассматривать только его шумовую ЧМ. Последняя слагается из двух независимых составляющих, собственных шумов ГУН и шумов, попадающих в цепь управления (на его вход) извне, т. е.

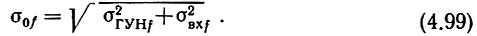
Первое слагаемое под радикалом (4.99) сильно изменяется для различных типов ГУН и может быть измерено (например, по методике [158]).

Допустимое шумовое напряжение на управляющем входе ГУН

Допустимая мощность шума на входе ГУН

С другой стороны, мощность шума линейной части схемы

Решая совместно (4.100), (4.101) и (4.102), получаем

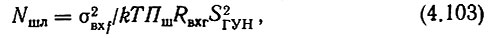
где шумовая полоса

Если полоса пропускания кольца ФАПЧ, определяемая при υ > 50

больше F_{м макс}, то в (4.103) нужно учитывать 2П_ФАПЧ, определяемую из (4.105). Таким образом, задача сводится к нахождению N_шл.

Воспользуемся выводами широко известной теории шумящих четырехполюсников (например, [159]) и составим уравнение, описывающее коэффициент шума линейной части системы (до ГУН). Считая, что шумовые характеристики гетеродинирующих колебаний, поступающих на смесители, учитываются коэффициентами шума смесителей, и пренебрегая коэффициентами шума фильтров, запишем выражение для коэффициента шума линейной части устройства:

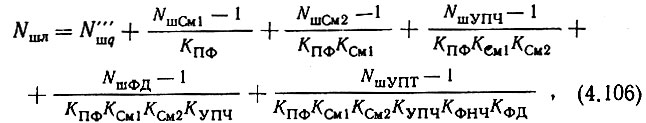
где К - коэффициенты передачи по мощности элементов схемы; N_ш - коэффициенты шума элементов схемы.

Чтобы воспользоваться ф-лой (4.106) для практических целей, необходимо знать порядок входящих в нее величин. Если примерные значения всех коэффициентов передачи и коэффициентов шума усилителей известны, то коэффициенты шума смесителей и фазавого дискриминатора необходимо выяснить. Задача осложняется тем, что при нахождении коэффициентов шума смесителей должны учитываться шумовые свойства гетеродинирующих колебаний, требования к которым и являются частью предмета выяснения в общей постановке вопроса.

Итак, коэффициент шума смесителя N_{ш См} зависит от собственного коэффициента шума N'_{ш См} и от шумовых характеристик гетеродинирующего колебания:

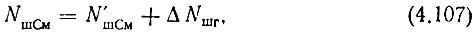
где ΔN_шг - составляющая коэффициента шума смесителя, обязанная своим появлением коэффициенту шума гетеродина.

Собственный коэффициент шума полупроводникового смесителя N'_{ш См} подробно исследован в ряде работ [129], [140], [159], [161] и др. Он зависит от многих факторов, в том числе от параметров диода и амплитуды гетеродинирующего колебания. При оптимальном согласовании входа и выхода смесителя, оптимальной мощности гетеродина (Р_г ≈ 0,3÷ 1 мВт) и применении современных полупроводниковых диодов собственный коэффициент шума смесителя оценивается величиной 8-10.

Остановимся на одном противоречии. Для уменьшения времени задержки в кольце ФАПЧ желательно, чтобы коэффициент усиления УПЧ был минимально возможным, т. е. при заданном значении ΔF_уд напряжение опорной частоты должно быть максимальным. С другой стороны, как было показано выше, для уменьшения влияния на работу устройства побочных составляющих в гетеродинном колебании параметр h, а следовательно, и мощность гетеродина нужно стремиться увеличивать. К последнему выводу приходит также автор статьи [162]. Однако, как уже отмечалось, для получения минимального коэффициента шума смесителя N'_{ш См} мощность гетеродина должна быть оптимальной, т. е. ее значительно увеличивать нельзя. Правда, так как кривая зависимости N_{ш См} = f(P_г) имеет нечетко выраженный минимум, крутой подъем в сторону уменьшения мощности Р_г и более пологий подъем в сторону ее увеличения, для одновременного удовлетворения требованиям и по подавлению побочных составляющих, и по шумовым характеристикам мощности гетеродина следует приближать к значению 1 мВт (здесь и выше речь шла о мощности гетеродина, приходящейся на один диод смесителя).

Что же касается влияния на коэффициент шума смесителя шумов гетеродина, то до 1965 г. этот вопрос в литературе был освещен недостаточно. В различных работах приводились отдельные экспериментальные данные, из которых следовало, что в коротковолновой части сантиметрового диапазона коэффициент шума однотактных смесителей увеличивается за счет шумов гетеродина на 1-3 дБ, с увеличением длины волны эта цифра уменьшается, а применение балансных смесителей приводит к снижению влияния шумов гетеродина примерно на порядок [140], [159]. Однако все эти данные, хотя и являются полезными, но не дают возможности исчерпывающе предъявить требования к шумовым характеристикам колебаний 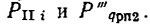Лишь в 1965 г. была опубликована статья [163], в которой автор достаточно полно освещает рассматриваемый вопрос. Воспользуемся основными выводами этой работы, в частности, ф-лой (10), которая записывается следующим образом:

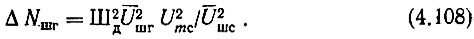
Здесь Ш_д - шумовой параметр диода, в свою очередь, зависящий от его параметров а и ρ_д и амплитуды напряжения гетеродина; U_mc - амплитуда напряжения "сигнала" на входе смесителя; 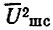- средний квадрат шумового напряжения на "сигнальном" входе смесителя; 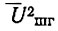- средний квадрат шумового напряжения гетеродина.

Современные смесительные диоды имеют а ≈ (15-25) 1/В и ρ_д ≈ 5⋅10^-7÷5⋅10^-3 (меньшие значения имеют кремниевые диоды, а большие - германиевые). Параметр Ш_д определяется из графика рис. 4.8, заимствованного из приводимой статьи. Если гетеродинирующее колебание задано не амплитудой напряжения U_mг, мощностью Р_г, то для пользования графиком нужно определить 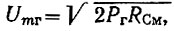где Р_См - входное сопротивление смесителя.

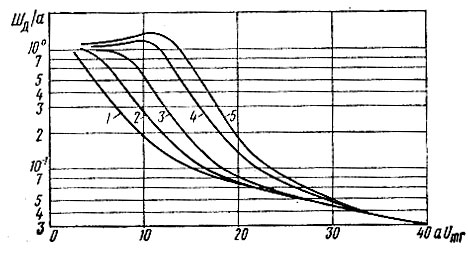
Рис. 4.8. К расчету параметра Ш_д смесителей: 1 - ρ_д = 5.10^-3, 2 - ρ_д = 5.10^-4, 3 - ρ_д = 5.10^-5, 4 - ρ_д = 5.10^-6, 5 - ρ_д = 5.10^-7

Однако выражение (4.108) неудобно для расчетов. Преобразуем его. Величины 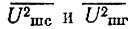пропорциональны мощностям шума "сигнала" и гетеродина соответственно. С другой стороны, эти шумы действуют на одинаковых сопротивлениях и в одинаковых полосах частот. Поэтому в соответствии с (4.102) отношение квадратов этих напряжений можно заменить отношением коэффициентов шума. Кроме того, 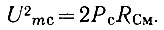С учетом этих замечаний (4.108) можно записать в виде

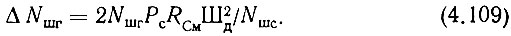
В правой части (4.109) пока неизвестны две величины, и если 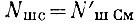определяется коэффициентом шума смесителя (смеситель считается согласованным на сигнальном входе и на выходе), то N_шг предстоит определить.

Так как шумы всех колебаний, подающихся на входы декады, преимущественно определяются шумами эталона частоты, а их интенсивность воздействия на кольцо ФАПЧ отражается соответствующими коэффициентами шума 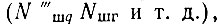то, учитывая, что шумовые девиации на входах кольца ФАПЧ в коэффициенты умножения раз больше шумовой девиации эталона частоты σ_q0f, можно утверждать, что отношение коэффициентов шума колебаний равно квадрату отношения частот этих колебаний χ². Так, для рассматриваемой декады частота гетеродина первого смесителя 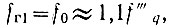следовательно,

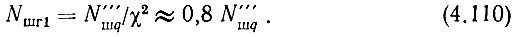
Частота гетеродина второго смесителя 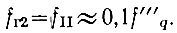Поэтому

Так как параметры обоих смесителей примерно одинаковы, то из (4.111) следует, что шумами гетеродина второго смесителя, т. е. шумами декады десятков в общем шумовом балансе системы, можно пренебречь.

Подставим (4.110) в (4.109):

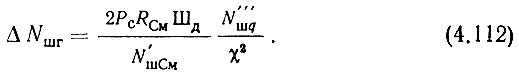
Учитывая (4.112) в (4.107), получаем

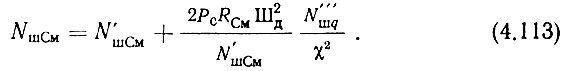
Теперь можно вернуться к выражению (4.106) и несколько упростить его. Обычно K_ПФ ≈ 0,5, К_См1 ≈ К_См2 ≈ 0,1, К_ФНЧ ≈ К_ФД ≈ 1, К_УПЧ ≈ 10⁶÷10⁷, а N_{ш ФД} ≈ N_{ш См} ≈ 8÷10 и N_{ш УПТ} ≈ N_{ш УПЧ} ≈ 3÷10. Следовательно, пятое и шестое слагаемые правой части (4.106) пренебрежимо малы по сравнению с первыми четырьмя. Таким образом,

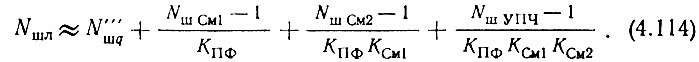
Подставим в (4.114) выражение (4.113), учтем замечание относительно (4.111), и так как все составляющие, кроме N'''_шq, известны, разрешим полученное уравнение относительно коэффициента шума наиболее высокочастотного выхода МОЧ. При этом получим следующее выражение:

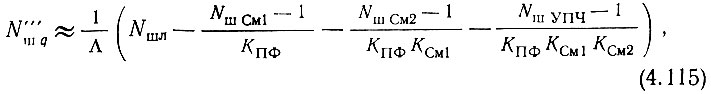
где для сокращения обозначено

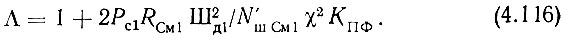
При расчете целесообразно обеспечить оптимальное распределение "веса" шумовых характеристик. В технике связи введен критерий [164], согласно которому следует стремиться к тому, чтобы шумовая температура приемника составляла не более 0,1 от шумовой температуры антенны. Трансформируя это положение к данному случаю, можно утверждать, что желательным является соотношение

или, другими словами, синтезатор должен быть спроектирован таким образом, чтобы шумы на выходе системы ДКСЧ определялись главным образом шумами эталона частоты.

Выше были рассмотрены шумовые характеристики декады сотен при разомкнутом кольце ФАПЧ. Замкнутое кольцо, как известно, является эквивалентным фильтром верхних частот для флуктуаций частоты (фазы) ГУН и эквивалентным фильтром нижних частот для флуктуаций частоты (фазы) колебаний опорных частот. Для шумов полоса пропускания эквивалентного ФНЧ является полосой пропускания ФАПЧ (П_ФАПЧ). В ее пределах собственные шумы ГУН ослабляются в коэффициент передачи раз, т. е. практически с ними можно не считаться. Шумы же устройства управления проходят на вход ГУН, модулируют его по частоте и, таким образом, оказываются в выходных колебаниях системы ДКСЧ. За пределами полосы пропускания ФАПЧ, наоборот, шумы устройства управления подавляются, а собственные шумы ГУН проходят на выход системы. Таким образом, для замкнутого кольца ФАПЧ выражение (4.99) не справедливо. Оно должно быть заменено следующими неравенствами:

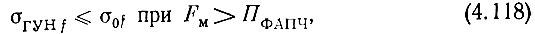
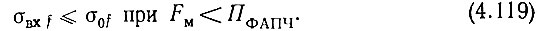
Рассмотрим условия выполнения неравенства (4.119), имея в виду, что во внимание принимается только шумовая ЧМ, которая является узкополосной.

Так как выражения (4.88), (4.93) и (4.102) справедливы для любой точки схемы, то, учитывая (4.104), можно записать, что в пределах полосы пропускания кольца ФАПЧ декады сотен

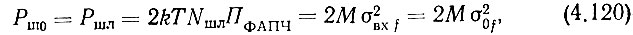
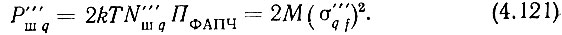
В этих выражениях коэффициент М принят одинаковым, так как обе мощности действуют на одинаковых преобразователях частота - напряжение и примерно равных нагрузках.

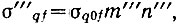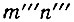Разделим (4.121) на (4.120) и учтем, что где - общий коэффициент умножения частоты эталона до значения опорной частоты декады сотен. Тогда

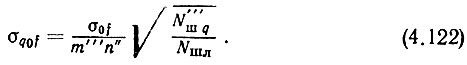
Итак, для снижения на выходе системы шумов до заданного уровня необходимо обеспечить выполнение неравенства (4.118) и получение σ_q0f в соответствии с ф-лой (4.122).

Рассмотрим особенности расчета шумовых характеристик пассивного многодекадного синтезатора. Для этого, как и ранее, достаточно рассмотреть лишь выходную декаду (рис. 4.7б). Так как здесь речь идет об узкополосной ЧМ (ψ_f << 1), то все элементы, входящие в эквивалентную схему, можно относительно шумов считать линейными. Поскольку неизвестно, на каком преобразователе частота - напряжение и на какой нагрузке действуют шумы синтезатора, то воспользоваться для анализа выражениями (4.98) и (4.94) не представляется возможным. С другой стороны, в системе нет и такого преобразователя напряжение - частота, как ГУН. Поэтому для определения коэффициента шума декады (а с ней и всего синтезатора) воспользуемся следующим приемом.

Пусть шумовая побочная составляющая Р_{ш б}, частота которой отстоит от несущей на F_{M макс}, занимает по спектру 1 Гц. Тогда ввиду малости ψ_f Р₀/Р_{ш б} = (U₀/U_{ш б})² = 4F²_{м макс}/Í_f0⋅1. Но Í_f0 = σ²_0f/F_{М макс}. Поэтому

С другой стороны, мощность шума в полосе 1 Гц

Приравняв правые части выражений (4.123) и (4.124), определим коэффициент шума системы

Теперь аналогично (4.106) можно записать

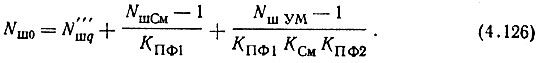
Так как коэффициенты передачи звеньев системы и коэффициенты шума усилителя мощности и смесителя известны, то из (4.126) можно определить максимально допустимый коэффициент шума МОЧ:

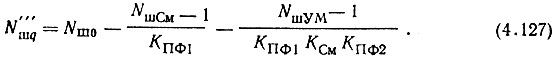
Используя методику анализа выражений (4.120) и (4.121), получим максимально допустимое значение дисперсии шумов МОЧ:

Допустимый коэффициент шума декады десятков можно определить из (4.109) как N_{ш II} = N_{ш г}, задавшись величиной ΔN_{ш г} (например, ΔN_{ш г} = 0,1 N_{ш См}). Однако из (4.111) следует, что в десятичных системах шумами декады десятков можно пренебречь и при расчетах значение коэффициента шума, полученное из (4.127), можно представить как требование к коэффициенту шума МОЧ. Если же система двоичная, в которой неравенство χ >> 1 не выполняется, то учет шумов младших ячеек обязателен. В этом случае целесообразно использовать в качестве множителя в левой части (4.127) выражение (4.116).