4.5. Анализ шумовых характеристик цифровых синтезаторов

Воспользуемся методикой, изложенной в предыдущем параграфе и проанализируем шумовые характеристики однокольцевого цифрового синтезатора СВЧ, структурная схема которого изображена на рис. 3.1б. Эквивалентная схема для расчета шумов представлена на рис. 4.9. По сравнению с эквивалентной схемой декады с аналоговой ФАПЧ (см. рис. 4.7а) схема рис. 4.9 имеет две особенности: во-первых, как указывалось в предыдущей главе, шумовая полоса ее ограничивается как минимум половинной частоты f_{q пр3} (3.29) и, во-вторых, из-за наличия существенно нелинейного элемента в виде ДПЧ, линейной можно считать лишь часть устройства до входа этого делителя. Поэтому, так как в пределах полосы пропускания кольца ЦФАПЧ собственные шумы ГУН практически полностью компенсируются, шумовая характеристика синтезатора σ²_0f определится шумами устройства управления, т. е.

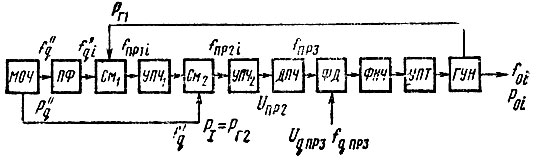
Рис. 4.9. Эквивалентная схема для расчета шумовых характеристик цифрового синтезатора СВЧ

Как и ранее, за пределами полосы пропускания

Шумы устройства управления слагаются из двух некоррелированных компонент: шумов колебаний опорной частоты f_{q пр3} и шумов с выхода ДПЧ.

Как нетрудно представить, девиация частоты (фазы) на любом входе фазового дискриминатора вызовет такое изменение абсолютной величины частоты (фазы) ГУН, которое, будучи разделенным в cυ раз, приведет к компенсации указанного возмущения. Таким образом, шумовая девиация частоты на выходе синтезатора за счет шумов колебаний опорной частоты, подаваемых на ФД.

Шумы на входе формирователя ДПЧ вызывают шумы на выходе ДПЧ в виде флуктуаций временного положения фронта (спада) импульсов выборки σ_τ (по сравнению с этими шумами триггерными шумами ДПЧ можно пренебречь). Если умножить ат на крутизну характеристики ФД, то получим флуктуации управляющего напряжения ГУН, которые будучи умноженными на крутизну характеристики ГУН дадут флуктуации частоты на выходе синтезатора. Таким образом, шумовая девиация на выходе синтезатора за счет шумов на входе ДПЧ

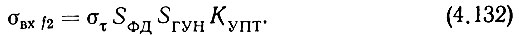
Заметим, что поскольку σ_τ выражается в секундах, крутизна характеристики ФД должна иметь размерность [В/с], для чего обычно применяемое значение крутизны в [В/рад] следует умножить на 2πf_{q пр3}.

Дисперсия суммарных частотных шумов синтезатора определяется как сумма дисперсий шумов (4.131) и (4.132):

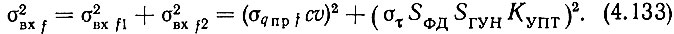
Для определения σ_τ воспользуемся выводами [165]. Выражение (10) этой работы в принятых здесь обозначениях для случая cυ >> 1 имеет вид

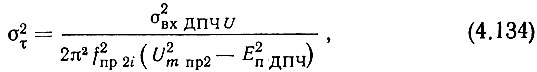
где σ_{вх ДПЧ U} - дисперсия напряжения шумов на входе ДПЧ (на выходе УПЧ); E_пДПЧ - пороговое напряжение формирователя импульсов ДПЧ; U_{m пр2} - амплитуда напряжения промежуточной частоты.

Очевидно, и допустимая амплитуда входного напряжения U_{m пр2} и пороговое напряжение формирователя определяются примененными в ДПЧ элементами, выбор типов которых для СВЧ синтезаторов обычно бывает невелик. Поэтому определяющим в (4.134) является уровень шумов на выходе линейной части устройства σ_вхДПЧU.

Так как шумы на входе ДПЧ определяются как шумами колебаний опорных частот f"_q и f'_q, так и собственными шумами линейной части кольца ЦФАПЧ, то определим коэффициент шума линейной части N_шл.

Мощность шума на входе ДПЧ, с одной стороны, определяется выражением (4.102), а с другой - формулой

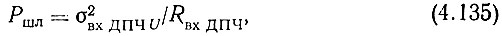
где R_вхДПЧ - входное сопротивление ДПЧ.

Приравняв правые части (4.102) и (4.135), получим

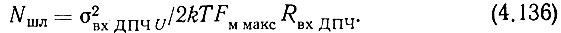
Подставим в (4.136) значение σ²_вхДПЧU из (4.134):

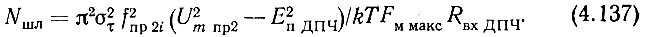
По аналогии с (4.106) можно записать

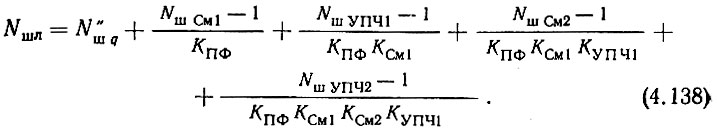
По-прежнему коэффициенты шума смесителей будем представлять по (4.107) и определять по методике, предложенной в [163] и подробно изложенной в предыдущем параграфе. По аналогии с (4.115) запишем выражение для определения коэффициента шума колебаний частоты f"_q

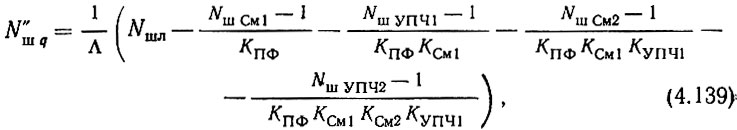
где Λ определяется из (4.116).

При написании (4.139) не учитывалось, что и в рассматриваемой системе для коэффициента шума гетеродинирующего колебания, подаваемого на второй смеситель, справедливо соотношение (4.111), т. е. шумами колебаний опорных частот f'_q можно пренебречь. Как и ранее [ф-ла (4.117)], желательно так проектировать систему, чтобы основная доля шумов определялась шумами колебаний опорных частот f"_q.

Определив по (4.139) коэффициент шума N"_шq, найдем дисперсию шумов колебаний опорных частот f"_q. Для этого воспользуемся анализом выражений (4.120) и (4.121), в результате чего получим

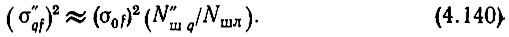
Итак, как следует из вышеизложенного, основным источником шума в системе является эталон частоты. При этом дисперсия шума эталона частоты σ²_q0f пересчитывается в дисперсии шумов всех трех колебаний опорных частот через квадраты отношений этих частот к частоте эталона f_q0. Поэтому расчет необходимого значения σ²_q0f можно себе представить следующим образом. Из (4.134) определяется σ²_τ, затем из (4.137) находится N_шл. Далее, по выражению (4.140), находится дисперсия (σ"_qf)², а по ней определяется дисперсия σ²_q0f. Однако так как в (4.133) входит величина σ²_{q прf}, также зависящая от σ²_q0f, то расчет следует вести методом последовательных приближений, приняв в первом приближении σ²_{q прf} = 0.

Если цифровой синтезатор выполняется по двухкольцевой схеме ФАПЧ-ЦФАПЧ (рис. 3.5), то сначала рассчитываются шумовые характеристики выходного кольца ФАПЧ так, как было изложено в § 4.4, а затем при необходимости - шумовые характеристики кольца ЦФАПЧ по приведенной только что методике.