5.2. Анализ кольца аналоговой ФАПЧ многодекадных синтезаторов

Анализ и расчет параметров кольца аналоговой ФАПЧ и входящих в него элементов проведем на примере наиболее общей схемы активного многодекадного синтезатора СВЧ (рис. 5.1а). Функциональную схему кольца ФАПЧ, соответствующую структурной схеме рис. 5.1а, при малых фазовых ошибках слежения изобразим так, как представлено на рис. 5.1б. При этом пока не будем учитывать колебания опорных частот 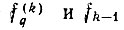в виде сигналов 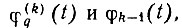показанных на эквивалентной схеме.

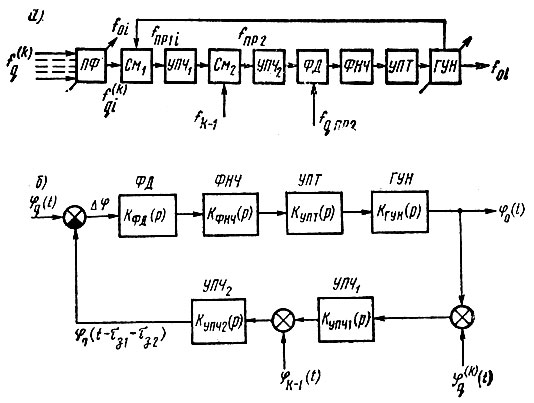
Рис. 5.1. Активный многодекадный синтезатор СВЧ с ФАПЧ: а) структурная схема выходной декады; б) функциональная схема кольца аналоговой ФАПЧ

Выясним вначале роль обоих УПЧ в динамике работы кольца. Если УПЧ узкополосны, то включение их в кольцо ФАПЧ эквивалентно введению инерционных звеньев. Тип этих звеньев и их параметры определяются низкочастотными эквивалентами УПЧ. Если же УПЧ достаточно широкополосны так, что их фазовые характеристики можно считать линейными и не учитывать изменения амплитуд выходных колебаний, УПЧ можно считать звеньями с чистым запаздыванием [166].

Широкополосность УПЧ в кольцах ФАПЧ синтезаторов СВЧ следует считать обязательным условием нормальной работы последних, так как время запаздывания τ₃ находится в обратной зависимости от широкополосности усилителей. В свою очередь, увеличение времени запаздывания приводит к сужению полосы пропускания системы или к уменьшению ее устойчивости. Весьма подробный анализ влияния запаздывания на работу кольца ФАПЧ приводится в [167]. Однако в этой работе учитывается динамика кольца ФАПЧ при очень большом запаздывании (порядка долей секунды). В кольцах же ФАПЧ, используемых в синтезаторах СВЧ, время запаздывания неизмеримо меньше, в связи с чем анализ можно существенно упростить.

С учетом последнего замечания раскроем смысл коэффициентов передачи отдельных звеньев функциональной схемы рис. 5.1б. В операторной форме коэффициент передачи фазового дискриминатора равен произведению коэффициента передачи К(Δφ) на частотнозависимый коэффициент К'_ФД(р) обязанный своим происхождением учету постоянной времени нагрузки ФД T_ФД. Таким образом,

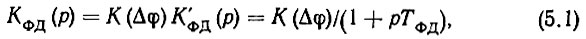
где р - оператор Лапласа.

Коэффициент передачи пропорционально-интегрирующего фильтра нижних частот, как известно, определяется выражением

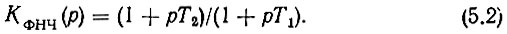
Коэффициент передачи усилителя постоянного тока есть также произведение коэффициента передачи по напряжению K_УПТ на частотнозависимый коэффициент передачи K'_УПТ(р), учитывающий в общем случае постоянные времени выхода УПТ T_УПТ и входа ГУН Т_ГУН:

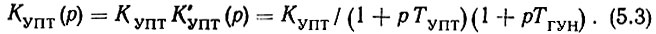
Коэффициент передачи ГУН определяется крутизной его характеристики управления S_ГУН. Однако он должен учитывать и интегрирующие свойства ГУН. Действительно, если на вход ГУН подать перепад напряжения, имеющего вид функции включения, то частота колебаний ГУН изменится также скачком, а фаза колебаний как интеграл от частоты будет изменяться по линейному закону. Это доказывает, что в фазовой системе, каковой является кольцо ФАПЧ, ГУН представляется чистым интегратором. Поэтому его коэффициент передачи

Наконец, так как УПЧ при приведенных выше условиях являются звеньями с чистым запаздыванием, их суммарный коэффициент передачи

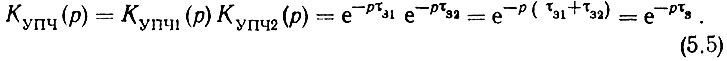
Таким образом, коэффициент передачи разомкнутого кольца ФАПЧ

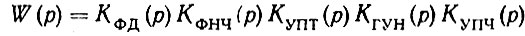
или после подстановки выражений (5.1)-(5.5)

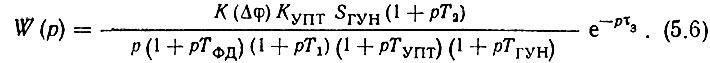
Рассмотрим физическую сущность произведения первых трех сомножителей числителя (5.6). Обычно характеристика ФД имеет либо треугольную (при равенстве амплитуд напряжений, подаваемых на ФД), либо косинусоидальную форму. Как будет показано ниже, при работе используется не весь диапазон изменения разности фаз от -π/2 до +π/2, а только его часть. Поэтому даже при косинусоидальной характеристике фазового дискриминатора ее рабочий участок можно считать квазилинейным, в связи с чем справедливо в стационарном режиме принять крутизну характеристики ФД максимальной и постоянной. С другой стороны, произведение максимального выходного напряжения ФД Е_уд на К_УПТ и S_ГУН дает полосу удержания системы. На основании этого

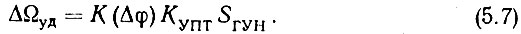
Подставляя (5.7) в (5.6), получаем

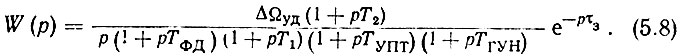
Вернемся к влиянию запаздывания в УПЧ на коэффициент передачи системы. Как показано в [168], с одной стороны, частота среза кольца ФАПЧ [W(Ω_ср) = 1] с пропорционально-интегрирующим ФНЧ

а с другой, - с точностью 15-20%

где П_ФАПЧу полоса пропускания кольца ФАПЧ в герцах по сигналам управления.

Совместное решение (5.9) и (5.10) дает

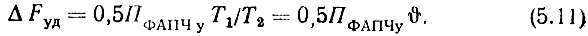
В гл. 2 отмечалось, что минимальная полоса пропускания УПЧ должна быть, по крайней мере, в два раза больше полосы удержания системы. Кроме того, там же указывалось, что обычно υ > 50. Поэтому, как правило, в синтезаторах СВЧ П_УПЧ ≥ 50 П_ФАПЧу.

Для этих условий (если полоса пропускания УПЧ в несколько десятков раз больше полосы пропускания кольца ФАПЧ) в [169] показано, что запаздывание в УПЧ нужно учитывать лишь при расчете устойчивости системы в виде уменьшения запаса но фазе:

где S_θПЧ - крутизна фазо-частотной характеристики тракта усиления промежуточной частоты.

В общем же случае фазовый сдвиг, вносимый n-каскадным УПЧ,

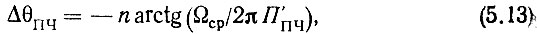
где П'_ПЧ - полоса пропускания одного каскада УПЧ.

Таким образом, в (5.8) экспоненциальный множитель при анализе можно опустить и учитывать его при расчете только в виде поправки (5.12). Кроме того, так как выход УПТ и вход ГУН соединены непосредственно, то элементы входа ГУН можно отнести к выходу УПТ и учитывать эти параметры суммарно в виде T_УПТ. С учетом этих замечаний выражение (5.8) окончательно запишется в виде

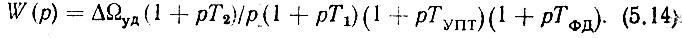
Если теперь вернуться к функциональной схеме кольца и учесть действие колебаний опорных частот f_q^(k) и f_k-1, то окажется, что соответствующие им сигналы управления φ_q^(k)(t) и φ_k-1(t) приложены, как и сигнал управления φ_q(t), ко входу фазового дискриминатора. Следовательно, все выражения и выводы, относящиеся к управлению по входу ФД, в равной мере справедливы и относительно управления по двум другим входам декады.

Для того чтобы основное уравнение ФАПЧ для данного случая привести к привычному виду (например, [25]), обозначим

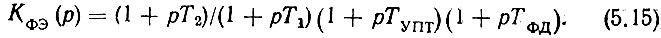
Тогда основное уравнение ФАПЧ можно записать как

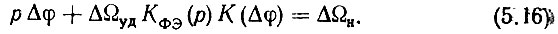
Здесь Δφ - мгновенная разность фаз колебаний на входах ФД, К(Δφ) - нормированная относительно максимального значения: характеристика ФД, принятая равной единице; ΔΩ_н - абсолютная статическая расстройка ГУН (абсолютное статическое отклонение частоты от номинального значения).

Из рассмотрения (5.16) вытекает, что К_ФЭ(р) есть коэффициент передачи некоего эквивалентного ФНЧ типа 1/3 по обычно принятой классификации фильтров. Эквивалентная реализация (5.15) и представляет собой последовательное соединение трех инерционных и одного форсирующего звеньев или в данном конкретном случае одного пропорционально-интегрирующего фильтра нижних частот с собственными частотами

и двух интегрирующих RС-фильтров с частотами среза

Передаточная функция по управлению замкнутого кольца ФАПЧ определяется [170] как

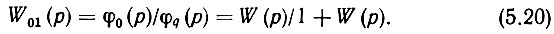
Заметим, что передаточные функции замкнутого кольца для изменений фазы и частоты равны между собой. Действительно,

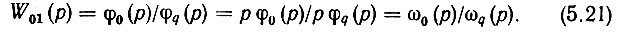
Таким образом, шумовые флуктуации частоты и фазы, а также побочные составляющие в виде продуктов паразитной угловой модуляции колебаний опорных частот передаются кольцом ФАПЧ на выход системы пропорционально функции W₀₁(p). Наоборот, собственные флуктуации фазы ГУН компенсируются кольцом обратно пропорционально передаточной функции по ошибке [170]:

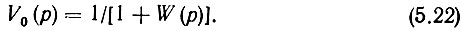
Следует, однако, отметить, что "полоса пропускания кольца ФАПЧ по ошибке" П_ФАПЧо (где эффективность компенсации ошибки еще не меньше граничной эффективности управления) не равна полосе пропускания по управлению. Если воспользоваться методом вычисления полосы П_ФАПЧу из [168] применительно к П_ФАПЧо, то можно получить соотношение:

или

Если приравнять знаменатель (5.20) нулю, то получится характеристическое уравнение кольца ФАПЧ:

Для упрощения дальнейших рассуждений, имея в виду, что постоянные времени Т_УПТ и Т_ФД существенно меньше Т₂ и Т₁ и мало влияют на динамику кольца, величины Т_УПТ и Т_ФД пока из рассмотрения исключим. В этом случае выражение (5.25) является квадратным уравнением относительно р. Если обозначить собственную частоту кольца

и коэффициент затухания

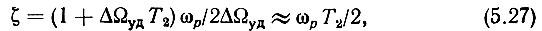
то характеристическое уравнение системы ФАПЧ запишется следующим образом:

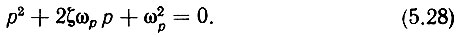
Корни ур-ния (5.28) суть

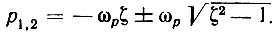
Если на вход системы подать скачок фазы, то в зависимости от коэффициента затухания ζ процесс установления фазы на выходе системы будет носить либо колебательный (ζ < 1), либо критический (ζ = 1), либо, наконец, апериодический (ζ > 1) характер. Этот процесс иллюстрируется графиками рис. 5.2 [105]. Как видно из рисунка, параметр ζ в значительной степени влияет на время установления синхронизма в системе. Минимальное время установления получается при ζ = 0,5. По кривым рис. 5.2 можно с достаточной точностью рассчитать это время. Действительно, из (5.26) и 10 (5.27) получим

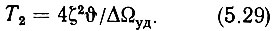
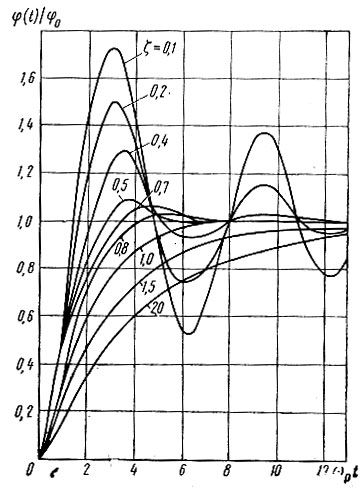
Рис. 5.2. К пояснению переходного процесса в кольце ФАПЧ

Но из (5.27)

а из графиков рис. 5.2

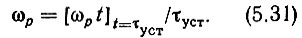
Решая совместно (5.30), (5.31) и учитывая (5.29), получим

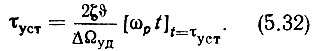
Положив ζ = 0,5 и найдя для этого значения из графиков (4,5÷5,5), по ф-ле (5.32) определим минимально возможное время установления синхронизма

Изложенное выше справедливо, однако, лишь для времени установления синхронизма в системе после броска фазы. Если же синхронизм устанавливается после скачка частоты, то процессы оказываются значительно сложнее. Действительно, если бы система ФАПЧ и при изменении частоты оставалась квазилинейной, то на основании (5.21) можно было пользоваться расчетными значениями времени установления, полученными из (5.32) и (5.33). Однако при изменениях частоты систему квазилинейной считать нельзя и при этом время установления синхронизма весьма существенно зависит от начальной расстройки ГУН [25]. Обычно можно ориентироваться на то, что это время на порядок больше значения, получаемого из (5.32). Таким образом, выражение (5.32) указывает лишь минимальный предел времени установления синхронизма и при прочих равных условиях может служить критерием для сравнения различных систем ФАПЧ по быстродействию.

Однако и эти рассуждения справедливы лишь в том случае, если статическая расстройка ГУН не превышает полосы захвата ФАПЧ. Полоса захвата системы с пропорционально-интегрирующим ФНЧ в соответствии с [25] выражается как

т. е. обычно в 7-10 и более раз уже полосы удержания. Как правило, для нормальной работы системы этого недостаточно, так как статическая начальная расстройка ГУН может быть лишь немногим меньше полосы удержания.

В гл. 1 указывалось, что для преодоления этой трудности можно использовать либо систему ЧФАПЧ, либо применить специальную схему поиска, которая автоматически вводит систему в пределы полосы захвата. Последняя система обычно называется поисковой системой ФАПЧ. Для осуществления поиска меняется частота ГУН со скоростью L_п [Гц/с], не превышающей определенного значения. При этом следует помнить, что с увеличением уровня шума на выходе фазового дискриминатора при одинаковой вероятности захвата скорость поиска приходится уменьшать.

Следует также отметить, что характеристики захвата являются функцией коэффициента затухания кольца [169]. Они оказываются лучшими при ζ = 0,5 и с увеличением ζ ухудшаются незначительно. С уменьшением затухания (ζ < 0,5) растет колебательность системы и процесс захвата резко ухудшается. С другой стороны, увеличение отношения полосы пропускания УПЧ к полосе пропускания ФАПЧ улучшает характеристики захвата, допуская увеличение L_п. Например, увеличение этого отношения от 6 до 20 дБ позволяет повысить скорость поиска в 1,8 раза [169].

В [169] приводится расчетная формула для скорости поиска, полученная экспериментально (как отмечается в [25], теоретический анализ поисковых систем ФАПЧ чрезвычайно сложен). Эта формула справедлива для вероятности захвата, равной 90%, и для ζ ≥ 0,5:

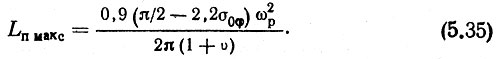
где σ_0φ - среднеквадратичное значение девиации фазы на выходе кольца [рад]; υ - относительный выброс фазы в градусах, зависящий от затухания (рис. 5.3), а L имеет размерность Гц/с.

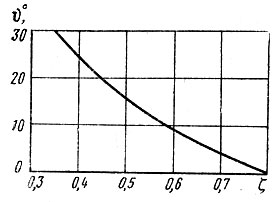
Рис. 5.3. Зависимость относительного выброса фазы от коэффициента затухания кольца ФАПЧ

Ранее было принято из-за малости постоянных времени Т_УПТ и Т_ФД при анализе их не учитывать. Как будет показано ниже, для устойчивой работы системы эти постоянные времени, действительно, должны быть малы. Однако повышение за счет их влияния разрядности эквивалентного ФНЧ от 1/1 до 1/3 приводит к появлению выброса характеристики передачи ФАПЧ, расположенного вблизи верхней границы полосы пропускания системы. Величина этого выброса возрастает по мере роста статической расстройки, т. е. по мере удаления рабочей точки ФД от середины характеристики. Наличие выброса АЧХ в полосе пропускания подчеркивает помехи, воздействующие на элементы системы, расположенные между ФД и ГУН, например фонов.

С. В. Трифонов рассчитал зависимость величины выброса частотной характеристики замкнутого кольца ФАПЧ от относительной статической расстройки для ФД с косинусоидальной характеристикой (рис. 5.4). Задавшись допустимым подчеркиванием указанных помех и зная максимально возможную величину статической расстройки ГУН, по графику можно определить необходимое расширение полосы удержания системы. Из графика, в частности, видно, что если допустить подчеркивание помех даже на 3 дБ, то полосу удержания необходимо расширить на 43% по сравнению со значением, необходимым для компенсации погрешности частоты ГУН. Другими словами, для данного примера характеристику ФД в работе можно использовать только на ±63°. Указанное явление и позволяет считать систему квазилинейной.

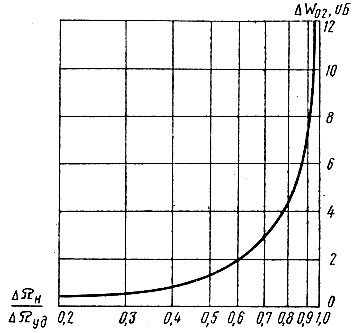
Рис. 5.4. Зависимость выброса частотной характеристики замкнутого кольца ФАПЧ от начальной расстройки

Перейдем к изложению основ расчета кольца ФАПЧ и входящих в него элементов. Будем ориентироваться на частотный метод расчета на базе логарифмических амплитудно-частотных (ЛАЧХ) и фазо-частотных (ЛФЧХ) характеристик. Этот метод широко используется в теории и практике систем автоматического регулирования и, в частности, применительно к ФАПЧ освещен в работах [168], [169], [170] и др.

Одним из основных требований к системе ФАПЧ является ее устойчивость. Воспользуемся для оценки устойчивости системы критерием Найквиста. Применительно к отдельно построенным ЛАЧХ и ЛФЧХ системы рассматриваемого типа этот критерий может быть сформулирован следующим образом: система устойчива, если на частоте, при которой коэффициент передачи разомкнутой системы равен единице (0, дБ), фазовый сдвиг в ней оказывается по абсолютному значению менее π.

Учитывая, что 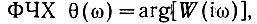на основании ф-лы (5.14) запишем: 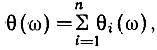или, раскрыв последнее выражение, будем иметь

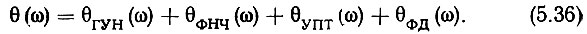
Подставим в (5.36) выражения для фазовых сдвигов и учтем сдвиг фазы, вносимый УПЧ (5.12),

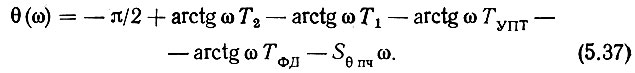
Однако для уверенной работы системы недостаточно только удовлетворить критерию Найквиста. Необходимо еще иметь определенный запас по фазе θ_З и по амплитуде (по усилению) W_З. Запас по фазе показывает, насколько ФЧХ не достигает значения -π при W(ω) = 1, а запас по амплитуде - насколько усиление разомкнутой системы меньше единицы при достижении ФЧХ значения -π. Обычно θ_З ≈ 30-45°, а W_З ≥ 10-15 дБ. При этом условие устойчивости может быть записано на основании (5.37) и с учетом (5.12) и (5.17)-(5.19) следующим образом:

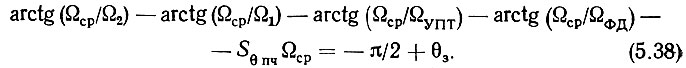
Важно отметить, что для обеспечения хорошей устойчивости системы в окрестности частоты среза наклон ЛАЧХ не должен превышать 20 децибел на декаду (дБ/дек), т. е. в этой окрестности инерционные свойства звеньев, входящих в систему, не должны суммироваться с интегрирующими свойствами ГУН. В противном случае наклон ЛАЧХ окажется равным 40 дБ/дек или 60 дБ/дек, а ЛФЧХ будет иметь значения, близкие к -180° или к -270° соответственно. Поэтому собственные частоты звеньев должны быть с достаточным запасом либо меньше Ω_ср, либо больше ее.

В связи с этим важным вопросом является выбор коэффициента затухания ζ. Выше было показано, что при ζ = 0,5 время установления синхронизма в системе минимально. Но при этом из (5.32) ζυω_p/πΔF_уп = 1, ω_р = 2πΔF_уд/υ. Но из (5.9) Ω_ср = 2πΔF_уд/υ, следовательно, при ζ = 0,5 ω_р = Ω_ср. С другой стороны, из (5.30) и (5.17) при ζ = 0,5 ω_р = Ω₂, т. е. при таком коэффициенте затухания Ω_ср = Ω₂ и система оказывается слабоустойчивой.

Если же выбрать ζ = 1, то из (5.30) ω_р = 2Ω₂, а из (5.32) и (5.9) Ω_ср = 2ω_p, т. е. Ω_ср = 4Ω₂, что, как будет показано ниже, является оптимальным. Правда, при этом минимально возможное время установления синхронизма увеличится примерно в 2,5 раза, но зато [ф-ла (5.35) и рис. 5.3] резко возрастает допустимая скорость поиска. Поэтому время перестройки системы на другую частоту не только не увеличится, но заметно сократится.

Типичные ЛАЧХ и ЛФЧХ для рассматриваемого случая изображены на рис. 5.5 (масштаб по осям абсцисс выбран логарифмическим). Как видно из рисунка, это ЛАЧХ второго типа. На частотах ω < Ω₁ действие ФНЧ еще заметно не проявляется и наклон характеристики - 20 дБ/дек обеспечивается за счет интегрирующих свойств ФАПЧ (за счет ГУН как интегратора). На частотах Ω₁ < ω < Ω₂ инерционные свойства пропорционально-интегрирующего ФНЧ суммируются с интегрирующими свойствами ГУН, наклон ЛАЧХ увеличивается на -20 дБ/дек и становится равным -40 дБ/дек. На частоте ω = Ω₂ начинают проявляться форсирующие свойства пропорционально-интегрирующего ФНЧ и ЛАЧХ снова получает наклон -20 дБ/дек, обусловленный интегрирующими свойствами ГУН. Такой наклон сохраняется до частоты ω = Ω_УПТ, начиная с которой заметно проявляются инерционные свойства эквивалентной нагрузки УПТ; наклон ЛАЧХ снова оказывается равным -40 дБ/дек. Наконец, начиная с частоты ω = Ω_ФД, к суммарному действию ГУН и нагрузки УПТ прибавляется инерционное действие нагрузки ФД и ЛАЧХ приобретает наклон -60 дБ/дек.

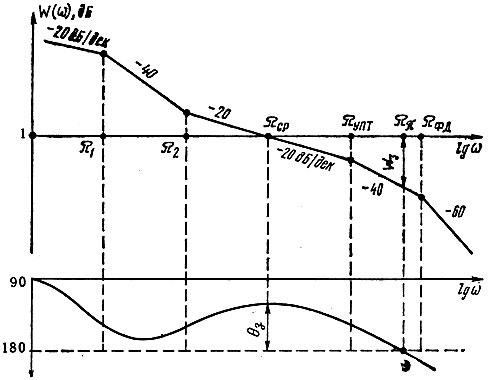
Рис. 5.5. ЛАЧХ и ЛФЧХ разомкнутого кольца ФАПЧ

Для ЛФЧХ, которая подчиняется выражению (5.37), существенными являются две частоты: Ω_ср, так как на этой частоте определяется запас по фазе θ_З, и Ω_π, так как здесь ЛФЧХ достигает значения -π и в дальнейшем остается по абсолютному значению больше его. На этой частоте определяется запас по амплитуде W_З. Методика определения θ_З и W_З ясна из рис. 5.5.

Сформулируем требования к ЛАЧХ:

- на частотах ω < Ω_ср значения W(ω) должны быть такими, чтобы в нужной степени компенсировались собственные шумы и фоны ГУН, спектральное распределение которых считается известным (измеренным);

- на частотах ω > Ω_ср значения W(ω) должны быть такими, чтобы шумы и помехи, создаваемые элементами кольца ФАПЧ и вносимыми в него вместе с колебаниями опорных частот, подавлялись до необходимого уровня;

- так как и W(ω) и собственные частоты звеньев из-за нестабильности параметров по частоте и во времени могут меняться, для обеспечения необходимой устойчивости Ω₂ и Ω_УПТ должны быть достаточно удалены от частоты Ω_ср.

Третье требование к ЛАЧХ предопределяет построение последней не в виде линии, а в виде зоны, ширина которой должна учитывать все нестабильности системы (главным образом, нестабильность ΔF_уд).

Подмена требований к коэффициентам передачи замкнутого кольца V₀(ω) и W₀₁(ω) требованиями к коэффициенту передачи разомкнутого кольца объясняется довольно просто. Действительно, из рассмотрения выражений для передаточных характеристик замкнутого кольца (5.22) и (5.20) на разных участках ЛАЧХ вытекает, что

- на участке 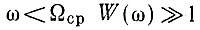и, следовательно, можно считать

- на участке 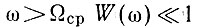и, следовательно,

- на частоте ω = Ω_ср W(ω) = 1; можно показать [168], что при этом

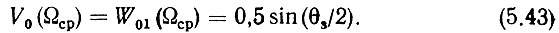
Таким образом, по известным параметрам ЛАЧХ разомкнутого кольца с достаточной для практики точностью можно определить параметры замкнутого кольца.

Обратим внимание на следующую особенность работы системы. Для подавления собственных шумов ГУН требуется, чтобы коэффициент передачи замкнутого кольца по ошибке не превышал единицы. Поэтому, если судить по ЛАЧХ разомкнутого кольца, шумы ГУН будут компенсироваться только до частоты Ω_ср. С другой стороны, внешние шумы будут проходить на выход системы в пределах полосы пропускания ФАПЧ, которая оказывается в два раза больше Ω_ср [ф-ла (5.10)]. Таким образом, может создаться впечатление, что в пределах полосы частот от Ω_ср до 2Ω_ср на выход системы проходят как некомпенсированные шумы ГУН, так и внешние шумы. Однако фактически из (5.43) следует, что при θ_З = 30-45° на частоте среза шумы ГУН еще ослабляются в 1,3-2 раза, а внешние шумы во столько же раз усиливаются.

Выше уже упоминалось о том, что частотное распределение шумов ГУН близко к колокольному, т. е. подчиняется закону f(x) = exр(-х²), в результате чего функция f(x) уменьшается на 60 дБ при изменении аргумента от нуля до х = 2,62. Таким образом, фактически интенсивность шумов ГУН быстро уменьшается с ростом частоты. Последнее дает возможность без большой ошибки считать, что в пределах полосы пропускания П_фАПЧу собственные шумы ГУН полностью компенсируются, а внешние шумы полностью проходят на выход.

Выше указывалось, что частоты среза звеньев Ω₂ и Ω_УПТ должны быть надежно удалены от частоты Ω_ср. В [168] доказывается, что приемлемый запас устойчивости по фазе обеспечивается в том случае, если выполняются следующие соотношения (применительно к данному анализу):

Что же касается частот Ω₁ и Ω_ФД, то первая рассчитывается с учетом необходимых значений υ и ω_р, а вторая должна выбираться из условия: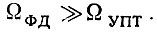

Приведенное выше выражение (5.38) для расчета запаса по фазе с учетом реальных соотношений в системе, а также ф-л (5.44) и (5.45) можно сделать более удобным для практического использования. Действительно, можно показать, что с большой точностью (1-2°) arctg(Ω_ср/Ω₂) ≈ 0,5π-Ω₂/Ω_ср и arctg(Ω_ср/Ω₁) ≈ 0,5π-Ω₁/Ω_ср, а также, что arctg(Ω_ср/Ω_УПТ) ≈ Ω_ср/Ω_УПТ и arctg(Ω_ср/Ω_ФД) ≈ Ω_ср/Ω_ФД. Подставив эти выражения в (5.38), получим

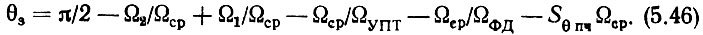
Наконец, следует заметить, что если реальные звенья системы почему-либо не могут иметь рассчитанных параметров, то строятся ЛАЧХ расчетная и ЛАЧХ по параметрам реальных звеньев, а затем берется их разность. По разностной ЛАЧХ подбираются дополнительные, так называемые корректирующие звенья, которые и включаются в реальную систему. При этом последняя будет иметь ЛАЧХ, близкую к расчетной.