
5.3. Анализ кольца ЦФАПЧ цифровых синтезаторов
Системы ЦФАПЧ являются импульсными системами автоматического регулирования (САР), т. е. системами прерывистого действия, несмотря на то, что импульсный характер колебания имеют только на одном участке замкнутой цепи. В этом плане они занимают промежуточное положение между аналоговыми системами ФАПЧ и системами ИФАПЧ (от последних они отличаются наличием ДПЧ и кратностью частот подаваемых на ФД колебаний, равной единице). Поэтому при анализе кольца ЦФАПЧ будем руководствоваться теорией импульсных САР, изложенной в [173], [174] и др.
В качестве объекта анализа выберем наиболее общую структурную схему цифрового синтезатора СВЧ (рис. 3.1б) с учетом изменений, внесенных в нее в гл. 3, 4 (применение безынерционного ФД типа "выборка-запоминание", включение в кольца ЦФАПЧ пропорционально-интегрирующего ФНЧ и т. д.). Однако прежде, чем перейти к функциональной схеме кольца ЦФАПЧ, выясним некоторые обстоятельства, связанные с неидеальностью безынерционного ФД. В гл. 3 упоминалось о том, что из-за неидеальности ФД типа "выборка-запоминание" коэффициент передачи напряжений с частотами nfq пр3 отличен от нуля. Обозначим этот коэффициент через χФД и найдем его допустимое значение.
Если на входе ФД действует напряжение с амплитудой Um ФД вх, а на его выходе из-за неидеальности - 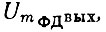 то
то
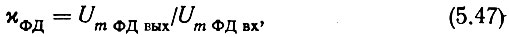
где 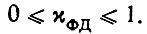
Применительно к обозначениям (5.47) выражение (4.21) запишется в виде
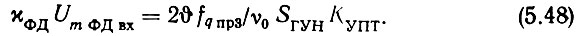
Но, с другой стороны, напряжение опорной частоты, соответствующее полосе удержания кольца ЦФАПЧ,
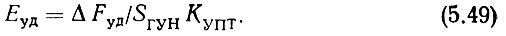
Разделим (5.48) на (5.49) и разрешим результат относительно χФД
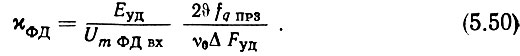
В стационарном режиме на входах ФД действуют два напряжения одинаковых частот fпр3 = fq пр3: импульсное напряжение выборки, амплитуда первой гармоники которого
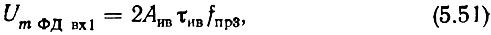
и напряжение опорной частоты fq пр3 с амплитудой

Как следует из выражений (5.50) и (5.51), допустить увеличение χФД при заданных fq пр3, ν0 и ΔFуд можно было бы за счет:
- уменьшения амплитуды импульсов выборки Аив, для чего потребуется применить в ФД более чувствительные ключи;
- уменьшения длительности импульсов выборки τив, для чего потребуется уменьшить постоянную времени заряда конденсатора запоминания;
- улучшения стабильности частоты ГУН, что позволит уменьшить ΔFуд.
Кроме того, для уменьшения влияния импульсов выборки на коэффициент гармоничности можно увеличить крутизну характеристики ФД, увеличив напряжение Еуд (с одновременным уменьшением KУПТ или SГУН). Однако, как следует из (5.52), эта мера не уменьшит уровень побочных составляющих за счет напряжения опорной частоты.
Универсальным средством увеличения коэффициента гармоничности колебаний является улучшение фильтрации, для чего необходимо увеличивать υ. Однако нельзя забывать, что при этом сужается полоса пропускания кольца со всеми вытекающими отсюда неприятными последствиями. Поэтому необходимо так строить ФД, чтобы обеспечить максимальное уменьшение χФД.
Перейдем к построению функциональной схемы кольца ЦФАПЧ. Если, как уже указывалось, в качестве исходной взять структурную схему рис. 3.1б, то функциональная схема кольца может быть изображена так, как представлено на рис. 5.6а. При этом, как и в предыдущем параграфе, вначале не будем учитывать колебания опорных частот f'q и f"q в виде сигналов управления φ'q(t) и φ"q(t). Из сравнения функциональных схем аналоговой ФАПЧ (рис. 5.16) и ЦФАПЧ (рис. 5.6а) видно, что в последней появился дополнительный элемент в цепи обратной связи - ДПЧ с коэффициентом передачи КДП(р). Так как этот элемент является делителем частоты, то, во-первых, его коэффициент передачи обратно пропорционален коэффициенту деления и, во-вторых, он способствует запаздыванию отклика системы на изменение параметра регулирования. Следовательно, коэффициент передачи ДПЧ

где τЗ3 - время запаздывания в ДПЧ.
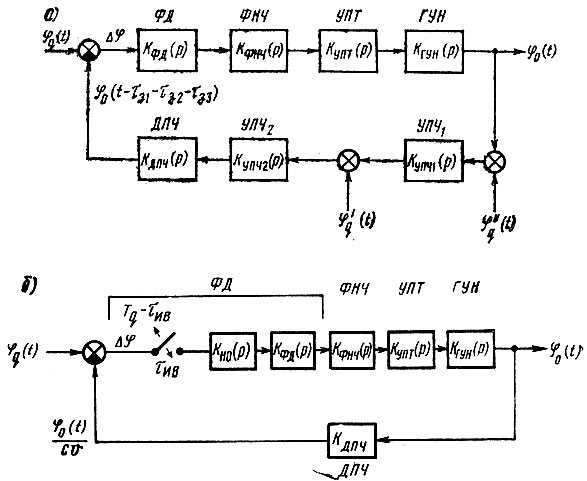
Рис. 5.6. Функциональные схемы кольца ЦФАПЧ цифрового синтезатора СВЧ: а) общая; б) упрощенная с фазовым дискриминатором типа 'выборка-запоминание'
В зависимости от структуры ДПЧ время запаздывания колеблется в больших пределах (от значения, близкого к нулю, до значения, превосходящего период регулирования Тq = 1/fq ФД). В настоящее время применяются такие структуры ДПЧ, в которых информация о состоянии ГУН за период Tq не накапливается. При этом время запаздывания определяется неидеальностью триггеров и формы запускающих импульсов. Так как в системах ЦФАПЧ СВЧ диапазона применяются ДПЧ на базе весьма быстродействующих триггеров, а неидеальность формы запускающих импульсов может проявиться только при запуске первого триггера или лишь в формирователе импульсов, то целесообразно временем τЗ3 в данном анализе пренебречь.
Как отмечалось выше, полосы пропускания УПЧ1 и УПЧ2 в цифровых синтезаторах СВЧ не могут быть уже т. е. при прочих равных условиях оказываются шире, чем в аналоговых системах. С другой стороны, в предыдущем параграфе было показано, что при анализе аналоговой ФАПЧ время запаздывания в УПЧ (5.5) целесообразно учитывать лишь при расчете запаса устойчивости системы по фазе (5.12), а самими звеньями, представляющими оба УПЧ в функциональной схеме кольца, можно пренебречь.
Таким образом, в цепи обратной связи функциональной схемы рис. 5.6а остается один элемент - ДПЧ с коэффициентом передачи

лишь условно зависящим от частоты. Действительно, с одной стороны, при перестройке частоты ГУН в пределах диапазона коэффициент деления меняется от сυмин до cυмакс, но, с другой стороны, при вариациях частоты (фазы) элементов кольца и выбранной (стационарной) рабочей частоте ГУН коэффициент деления ДПЧ оказывается также фиксированным и, следовательно, от частоты не зависит. Отсюда вытекают две предпосылки для анализа: при рассмотрении процессов в кольце на выбранной частоте диапазона синтезатора следует считать КДПЧ(р) = КДПЧ = 1/cυ = const, а сам анализ (расчет кольца) нужно проводить по меньшей мере дважды - при υмин и υмакс.
При составлении передаточных характеристик разомкнутого и замкнутого кольца следует помнить, что в цепи обратной связи, в отличие от кольца аналоговой ФАПЧ, появился элемент с передаточной характеристикой КДПЧ. В соответствии с определением, данным в [168], передаточной характеристикой разомкнутой САР называется отношение изображения выходной величины к изображению сигнала рассогласования при нулевых начальных условиях, т. е. в данном случае
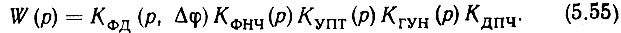
Однако для выражения передаточной характеристики замкнутой системы, содержащей элемент в цепи обратной связи, ф-ла (5.20) оказывается несправедливой. В этом случае можно записать
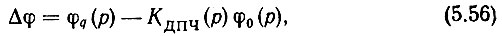
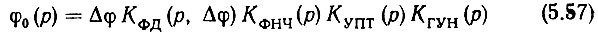
или, исключая из этих выражений Δφ и учитывая (5.55), получаем
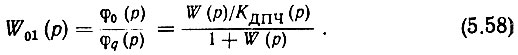
Выражение же (5.22) не изменится. Действительно, разделив, обе части равенства (5.56) на φq(p) и подставив в получившееся выражение (5.58), будем иметь
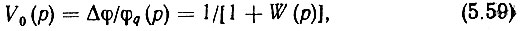
где W(p) определяется из (5.55).
Получив выражения (5.55), (5.58) и (5.59), можно было бы продолжить анализ по тому же плану, что и в предыдущем параграфе. Однако до сих пор здесь не учитывалось ни то, что система ЦФАПЧ является импульсной САР, ни то, что в состав ФД входит фиксатор нулевого порядка.
Рассмотрим вначале отличительные особенности импульсной САР. Выходной параметр системы меняется относительно входного непрерывно (в данном случае φ0 относительно φq). Но при этом на выходе фазового дискриминатора сигнал рассогласования представляется последовательностью импульсов, модулированных по закону изменения выходного параметра с периодом следования, равным Tq. Из гл. 3 вытекает, что в случае применения триггерного ФД происходит широтно-импульсная модуляция, а при использовании ФД типа "выборка-запоминание" - амплитудно-импульсная.
Схематически преобразование непрерывного сигнала рассогласования в импульсный (с АИМ) можно обозначить введением на входе системы импульсного элемента или модулятора (будем обозначать его ключом), за которым следует линейная часть системы. Так как импульсный элемент включается лишь на время длительности импульса с периодом следования Tq, то система является замкнутой только в моменты действия импульсов. В паузах же между импульсами система разомкнута после ФД, и изменение выходного параметра определяется лишь переходными процессами в линейной части системы. Таким образом, фазовый дискриминатор "выборка-запоминание" представим последовательным включением импульсного элемента (ключа), фиксирующего устройства, запоминающего значение управляющего напряжения во время действия предыдущего импульса выборки до прихода последующего и, как обычно, инерционного звена, учитывающего постоянную времени выходных цепей ФД.
Итак, на выходе ФД имеется импульсно-модулированный сигнал рассогласования, действующий в дискретные моменты времени nТq (n - натуральный ряд целых положительных чисел).
Отвлечемся от реальных импульсов выборки и положим, что на вход импульсного элемента подается непрерывный сигнал x(t) и последовательность дельта-функций δ(t-nTq), следующих с интервалами Tq. Как известно, δ(t-t0) = 0 при t ≠ t0 и δ(t-t0) = ∞ при t = t0, а также 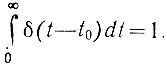 При этом сигнал на выходе импульсного элемента [174]
При этом сигнал на выходе импульсного элемента [174]
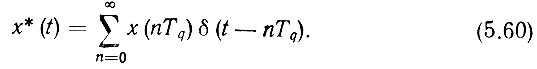
Этот же импульсно-модулированный сигнал можно записать в другой форме:
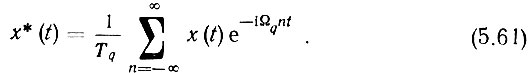
Этот сигнал может быть записан и в операторной форме. Однако в связи с тем, что сигнал во времени дискретен, его преобразование носит название дискретного преобразования Лапласа.
В теории САР показывается, что изображение (5.60) можно представить следующим образом:
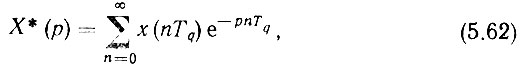
а (5.61) - соответственно
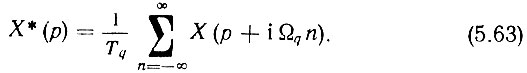
Из (5.62) и (5.63) следует, что дискретное преобразование Лапласа является периодической функцией с периодом Tq = 2π/Ωq = 1/fq ФД. Далее, из (5.62) видно, что Х*(р) изображает бесчисленное множество различных функций, совпадающих друг с другом в моменты времени nTq, т. е. нахождение оригинала X(t) по изображению Х*(р) невозможно. Кроме того, Х*(р) есть функция e-pTq, а не р, как при обычном преобразовании.
Выражения (5.60)-(5.63) легко применимы в данном анализе, если под символами X понимать амплитуды соответствующих напряжений.
Если в (5.63) заменить р на iω, то можно получить частотный спектр на выходе импульсного элемента в виде суммы отдельных спектров, каждый из которых повторяет форму огибающей X(iω). Если Ωq достаточно мала, то спектры будут накладываться друг на друга и выделить огибающую непрерывного сигнала станет невозможно. Теорема В. А. Котельникова устанавливает для идеальной системы предел

где Ωмакс - максимальная частота составляющей непрерывного колебания, точное воспроизведение которой может быть обеспечено при частоте следования импульсов Ωq. В случае не идеальной, а реальной системы знак равенства в (5.64) должен быть опущен.
Пользуясь изложенными выше положениями, найдем выражение для импульсных передаточных характеристик разомкнутого и замкнутого кольца ЦФАПЧ Заменим в (5.63) X на W. Тогда импульсная передаточная характеристика разомкнутого кольца запишется в виде
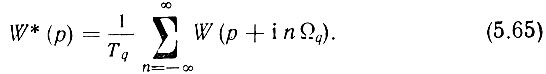
Подставим в (5.65) выражение (5.55)
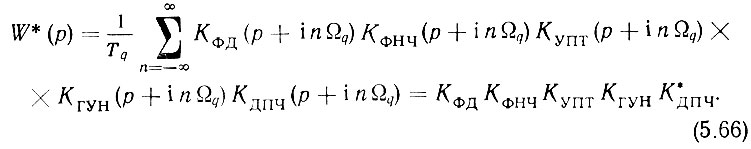
Последняя часть равенства (5.66) означает, что импульсная передаточная характеристика разомкнутого кольца берется от всех элементов совместно.
Практически требуется по известной характеристике W(p) путем обратного преобразования Лапласа определить W(t), а затем по известной характеристике W(t) найти дискретное преобразование Лапласа W*(p). Рассуждая аналогично и пользуясь (5.58) и (5.59), можно получить выражения для импульсных передаточных характеристик замкнутого кольца
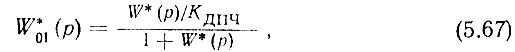
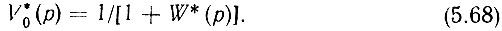
Для дальнейшего анализа приведем функциональную схему рис. 5.6а к окончательному виду (рис. 5.6б). На этом рисунке изображены элементы, передаточные функции которых известны. Исключением является фиксирующее устройство фазового дискриминатора, передаточную функцию которого обозначим, как и в гл. 3, Кн0(р). Найдем ее значение, имея в виду, что на выходе этого элемента образуются амплитудномодулированные импульсы длительностью Tq при импульсах на входе длительностью τив. Другими словами, фиксатор может быть представлен формирователем прямоугольных импульсов длительностью Tq. Такой импульс может быть, в свою очередь, представлен двумя единичными перепадами разных знаков, сдвинутых друг относительно друга на Tq: положительным 1(t) и отрицательным 1(t-Tq). Обычные (не дискретные) преобразования Лапласа этих функций суть 1/р и e-pTq/p соответственно.
Таким образом, изображение прямоугольного импульса, а следовательно, и передаточная функция фиксатора нулевого порядка
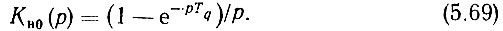
Теперь известны передаточные функции всех элементов функциональной схемы рис. 5.6б. Это дает возможность определить импульсную передаточную функцию разомкнутого кольца и построить ЛАЧХ и ЛФЧХ. По этим характеристикам можно определить степень устойчивости системы (запасы устойчивости по фазе и амплитуде), а также рассчитать характеристики элементов функциональной схемы и, если необходимо, дополнительных элементов, корректирующих логарифмические характеристики.
Наиболее сложным моментом расчета является нахождение импульсной передаточной характеристики разомкнутого кольца. Действительно, согласно изложенной выше методике необходимо осуществить обратное преобразование Лапласа от произведения коэффициентов передачи всех звеньев, входящих в функциональную схему, а затем произвести прямое, но уже дискретное преобразование Лапласа. Если принять во внимание, что в соответствии с произведением коэффициентов передачи в функциональную схему входит большое число звеньев, то становится очевидной громоздкость указанной операции.
Несмотря на это, в общем случае расчета систем ЦФАПЧ, особенно при больших значениях Tq (в цифровых синтезаторах диапазонов КВ и МВ), такой расчет проводить необходимо, иначе неминуемы значительные погрешности. С другой стороны, в цифровых синтезаторах СВЧ благодаря сравнительно большим значениям шага дискретности β0 и малым коэффициентам деления с фиксированного делителя, интервал регулирования Tq оказывается значительно меньшим по сравнению с постоянными времени большинства инерционных звеньев. Это усиливает фильтрующее действие линейной части системы и дает возможность выполнить ее приближенный расчет как аналоговой, считая, что на линейную часть поступает не импульсный, а непрерывный сигнал [174].
Однако такая постановка вопроса имеет одну особенность. Для ее учета рассмотрим частотный спектр импульсно-модулированного сигнала на выходе фиксирующего устройства (ФУ). В соответствии с (5.63) на входе ФУ действует напряжение
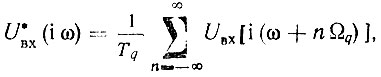
а на выходе ФУ с учетом (5.69) - напряжение
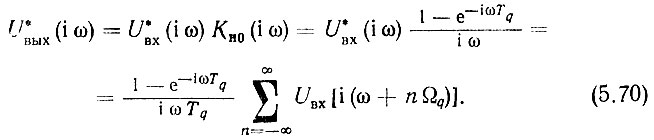
Преобразовав дробь перед знаком суммирования в (5.70), получим [174]
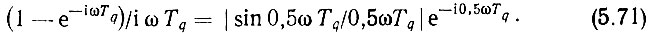
Подставим (5.71) в (5.70):
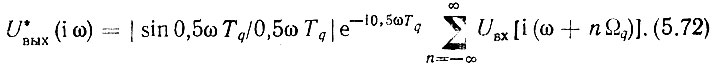
Выражение (5.72) показывает, что на выходе ФУ образуется бесконечный дискретный спектр, амплитуды составляющих которого пропорциональны sin 0,5ωTq/0,5ωTq, а фазы сдвинуты на 0,5ωTq. Таким образом,
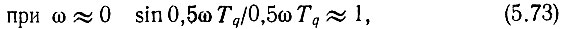
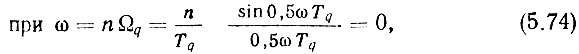
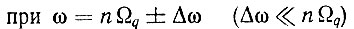
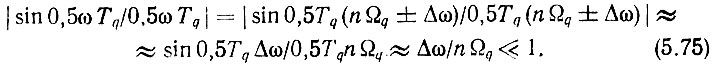
Анализ выражений (5.73)-(5.75) показывает, что напряжение на выходе ФУ равно входному вблизи нулевой частоты, отсутствует на частотах, точно кратных опорной частоте фазового дискриминатора и ее гармоник, и весьма мало в непосредственной близости от этих частот. Следовательно, идеальное ФУ восстанавливает закон аналогового сигнала на входе ФД, но вводит запаздывание этого сигнала во времени на 0,5Tq. Последнее на примере синусоиды иллюстрируется рис. 5.7.
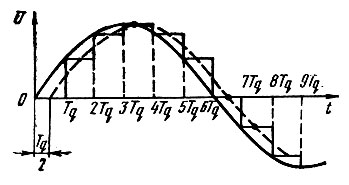
Рис. 5.7. К пояснению фазовой задержки в запоминающем устройстве фазового дискриминатора
Выше неоднократно подчеркивалось, что реальное фиксирующее устройство не столь значительно подавляет составляющие опорной частоты и ее гармоник, но для расчета системы, содержащей между ФД и ГУН фильтрующие элементы, это не очень существенно. Таким образом, для расчета в данном случае передаточную функцию фиксирующего устройства можно представить в виде

Систему ЦФАПЧ целесообразно рассчитывать с использованием ЛАЧХ и ЛФЧХ так же, как и аналоговую ФАПЧ, но с учетом выражений (5.54), (5.55), (5.58), (5.59) и (5.76). Выражение (5.76) необходимо учитывать при расчете ЛФЧХ и, в частности, при расчете запаса по фазе, имея в виду, что при ω = Ωср

Выражение (5.77) должно войти слагаемым в правую часть (5.37) и в левую часть (5.38). Можно воспользоваться и приближенным равенством (5.46).
Если теперь учесть, что в системе действуют еще два управляющих сигнала φ'q(t) и φ"q(t), соответствующие опорным частотам f'q и f"q, то окажется, что на функциональной схеме рис. 5.6б они оба приложены к одной точке - входу ДПЧ. Для этой точки ДПЧ оказывается в цепи прямой, а не обратной связи и, следовательно, передаточная функция замкнутого кольца ЦФАПЧ по управлению этими сигналами запишется следующим образом:
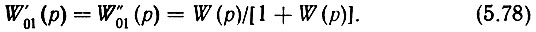
Пользоваться ЛАЧХ разомкнутой системы для определения характеристик замкнутой в случае ЦФАПЧ можно, но с большой осторожностью из-за наличия в цепи обратной связи ДПЧ. В предыдущем параграфе было показано [ф-лы (5.39)-(5.42)], что если известны частотные характеристики разомкнутой системы, то в полосах частот, представляющих практический интерес, с достаточной степенью точности можно судить о характеристиках замкнутой системы. Посмотрим, в какой степени это относится к кольцу ЦФАПЧ.
При малых значениях ω функция W(ω) >> 1 и из (5.58), (5.78) и (5.59) соответственно получаем:
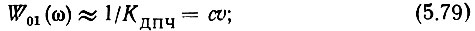


При больших значениях ω функция  Тогда
Тогда
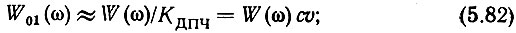


Выражение (5.79) показывает, что в пределах полосы пропускания кольца шумы в колебаниях опорной частоты fqФД пересчитываются на выход синтезатора, умножаясь на коэффициент деления ДПЧ (напомним, что в гл. 4 был получен такой же вывод по чисто физическим соображениям). Из (5.80) следует, что шумы в колебаниях опорных частот f'q и f"q в этой же полосе частот проходят на выход системы без изменения интенсивности, а из (5.84) получаем, что вне полосы пропускания кольца собственные шумы и фоны ГУН без ослабления проходят на выход синтезатора.
Таким образом, наиболее интересными для расчета являются выражения (5.81), (5.82) и (5.83). Первое из них показывает, что в пределах полосы пропускания собственные шумы и фоны ГУН ослабляются при замкнутом кольце в число раз, равное коэффициенту передачи разомкнутого кольца, который определяется из (5.55) с учетом того, что модуль коэффициента передачи идеального фиксатора равен единице.
Выражения (5.82) и (5.83) показывают степень подавления побочных составляющих, поступающих в кольца с колебаниями опорных частот. Но если в (5.83) фигурирует передаточная характеристика разомкнутого кольца, то в (5.82) эта характеристика оказывается умноженной на cυ >> 1, т. е. она является передаточной характеристикой разомкнутого кольца без учета элементов обратной связи.
Отсюда следует, что для выяснения количественных соотношений необходимо строить три ЛАЧХ замкнутого кольца: для W'01(ω), V0(ω) и для W01(ω), так как они являются разными функциями от W(ω). И если ЛАЧХ V0(ω) при W(ω) >> 1 и ЛАЧХ W'01(ω) при W(ω) << 1 эквивалентны ЛАЧХ W(ω), то ЛАЧХ W01(ω) в общем случае нужно строить, исходя из следующего равенства, полученного по (5.58):
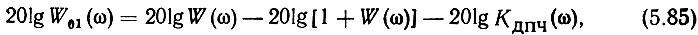
т. е. построить три ЛАЧХ, соответствующие правой части (5.85), и произвести указанные арифметические действия.
Упростить расчеты помогает частный случай: K(ω) = КДПЧ = 1/cυ = const, т. е слагаемое 20lgKДПЧ(ω) в (5.85) просто переместит на свою величину вверх ЛАЧХ разомкнутого кольца в области верхних частот, где W(ω) << 1:
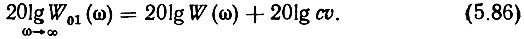
Наличие второго слагаемого в правой части (5.86) показывает, что побочные составляющие в колебаниях опорной частоты fq пр3 фактически ослабляются значительно меньше, чем это следует из расчетов ЛАЧХ разомкнутого кольца и те авторы, которые этого не учитывают, допускают большую ошибку.
Таким образом, если построить ЛАЧХ разомкнутого кольца (рис. 5.8), а затем сместить ее верх на 20 lg cυ, то левая часть несмещенной ЛАЧХ (от ω = 0 до ω = Ωср н - нижней частоты среза) будет характеризовать передаточную функцию V0(ω) замкнутого кольца, правая часть несмещенной ЛАЧХ (от ω = Ωср н до ω = ∞) - передаточную функцию замкнутого кольца W'01(ω), а правая часть смещенной ЛАЧХ (от ω = Ωср в - верхней частоты среза до ω = ∞) - передаточную функцию замкнутого кольца W01(ω).
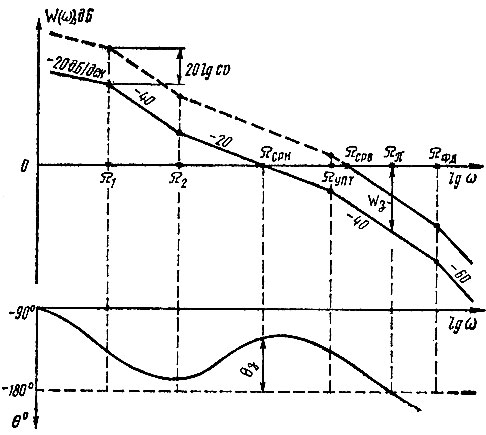
Рис. 5.8. ЛАЧХ и ЛФЧХ разомкнутого кольца ЦФАПЧ
Выше указывалось, что ЛАЧХ необходимо строить как для υмин, так и для υмакс. При этом следует иметь в виду, что несмещенная ЛАЧХ при υмакс занимает крайнее нижнее положение и, следовательно, характеризует минимальную компенсацию системой собственных шумов ГУН, а при υмин - крайнее верхнее положение и характеризует минимальное подавление побочных составляющих, поступающих в кольцо с колебаниями опорных частот f'q и f"q. Так как произведение W(ω)cυ фактически коэффициент деления ДПЧ не содержит, то это показывает, что с точки зрения подавления побочных составляющих одинаковых частот, поступающих по опорному входу ФД, системы аналоговой ФАПЧ и ЦФАПЧ идентичны (подразумевается, что частоты помех превосходят значение Ωср в).
Напомним, что так как ЛФЧХ зависит только от постоянных времени звеньев, все, изложенное в предыдущем параграфе о ее построении, остается в силе - ЛФЧХ разомкнутого кольца соответствует несмещенной ЛАЧХ. Естественно, поскольку устойчивость системы определяется по ЛАЧХ и ЛФЧХ разомкнутого кольца, то запас по фазе определяется на частоте Ωср н, а запас по усилению - по несмещенной ЛАЧХ при θ = -π, учитывающей разброс нестабильностей параметров системы.
Заметим, что так как характеристическое уравнение определяется передаточной функцией разомкнутого кольца, в которую входит КДПЧ = 1/сυ, то в выражения (5.26)-(5.33) нужно подставлять эквивалентную полосу удержания

Анализируя (5.10), можно показать, что полосы пропускания кольца ЦФАПЧ, как по управлению, так и по ошибке, сократились по сравнению с полосами аналогового кольца в cυ раз, хотя соотношения между ними, а также между ними и Ωср н сохранились прежними.

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
