7.2. Методика инженерного расчета системы ДКСЧ с многодекадным активным синтезатором

Перед началом расчета считаем заданными основные параметры системы ДКСЧ и выбранными структурную схему синтезатора в соответствии с рис. 2.9 и структурную схему МОЧ (см. гл. 6).

1. Расчет начинается с выбора частотного плана системы ДКСЧ. В зависимости от назначения системы ее частоты могут совпадать с несущими частотами радиолинии или быть смещены относительно последних. Взаимное расположение несущих частот и частот f₀ может быть односторонним нижним или верхним, когда все частоты f₀ смещены относительно несущих частот соответственно вниз или вверх, и двусторонним внешним или внутренним. При двустороннем внешнем расположении половина частот f₀ расположена ниже, а вторая половина - выше несущих частот. При двустороннем внутреннем расположении, наоборот, несущие частоты находятся по обе стороны от частот f₀. В этом случае в частотном плане несущих частот должен быть защитный интервал Z_н. При других расположениях также возможны один или несколько защитных интервалов между несущими частотами.

Задачей расчета частотного плана системы ДКСЧ является правильное расположение с точки зрения взаимных помех частот f₀ относительно несущих частот.

2. Определяем число дискретных частот системы. В общем случае если имеется Z_н, то при односторонних расположениях частот расчетное число частот системы α'₀ превышает заданное α₀:

Если же расположение частот двустороннее внутреннее или Z_н = 0, то α'₀ = α₀. При двустороннем внешнем расположении расчет следует проводить по (7.1), но при замене Z_н на Z₀ (Z₀ = П₀ - α₀β _{- частотный интервал между двумя группами частот f0).}

3. На основании α'₀ определяется число декад k (полных и неполных), входящих в систему. Так как α'₀ ≤ 10^k, то

При этом характеристика логарифма показывает число полных декад, а наличие ненулевой мантиссы указывает на необходимость иметь еще одну, неполную декаду. Заметим, что неполная декада должна быть самой высокочастотной.

4. Расчет частотообразования.

Определим шаг дискретности опорных частот

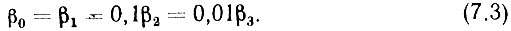
Вначале рассмотрим вариант, когда f₀ > f'''_q.

На частотном плане рис. 7.1 все величины для этого варианта подчеркнуты одинарной линией. На этом рисунке обозначены ΔП₀ - помехозащитные полосы по краям диапазона рабочих частот системы.

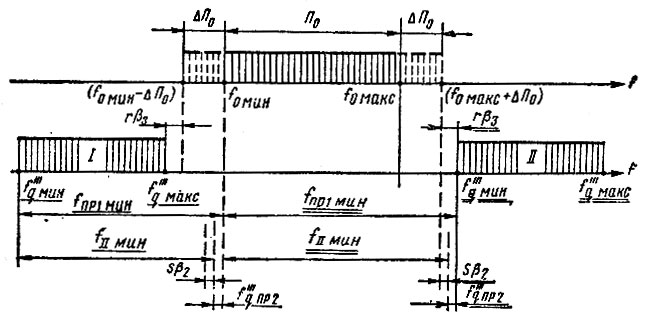
Рис. 7.1. Частотный план активного многодекадного синтезатора СВЧ

Для рассматриваемого варианта основное уравнение частотного плана

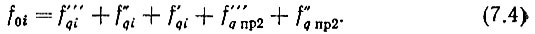
Если частота № 1 обозначается на табло как "001", то в соответствии с (7.4) 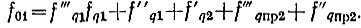Но сетки опорных частот являются гармониками опорных частот, поступающих на генераторы гармоник, 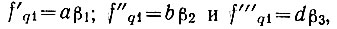следовательно, f'_q2 = (а + 1)β₁. Тогда с учетом (4.36)

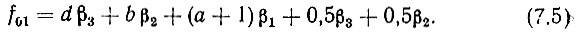
Согласно (2.44) 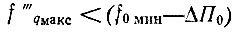или, превратив это условие в равенство,

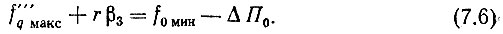
Число опорных частот старшей декады D = α'₀/β₃ (в случае дроби D округляется увеличением до целого числа).

С учетом последнего (7.6) запишется

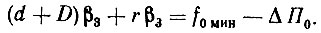
Откуда

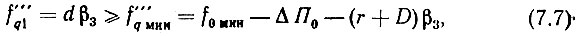
где r выбирается в соответствии с селективностью ПФ. Остальные опорные частоты декады

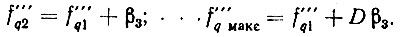
Приравняем значения f_{0 мин} = f₀₁ из (7.5) и (7.7). Тогда

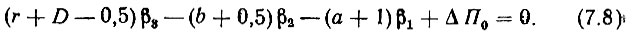
Но мы имели условие (2.29), в соответствии с которым f_{II мин} > П₀ + ΔП₀. Последнее неравенство превращается в равенство при

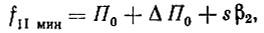
или

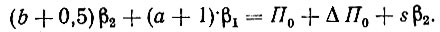
Подставим отсюда значение (b + 0,5)β₂ в (7.8). Тогда, после несложных преобразований,

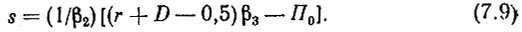
При проектировании системы желательно, чтобы порядок номеров гармоник в опорных частотах декад десятков и единиц был примерно одинаковым. Подставим в (7.5) a ≈ b. Тогда

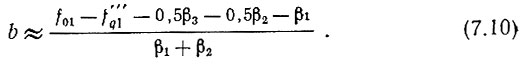
Округляем b до целого значения и определяем

Остальные опорные частоты декады

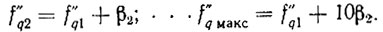
Из (7.5) имеем

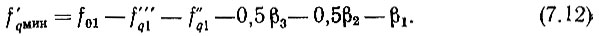
Остальные опорные частоты декады

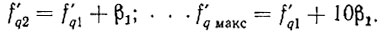
Рассмотрим второй вариант, когда 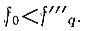На рис. 7.1 все величины для этого варианта подчеркнуты двойными линиями.

Для этого случая выражение (7.4) запишется следующим образом:

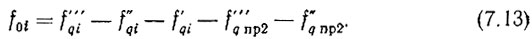
а выражение (7.5) примет вид

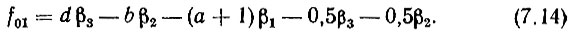
Для рассматриваемого варианта согласно второму условию (2.44) f'''_{q мин} > f_{0 макс} + ΔП₀ или, в виде равенства,

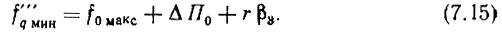
Но f_{0 макс} = f_{0 мин} + П₀. С учетом этого (7.15) запишется

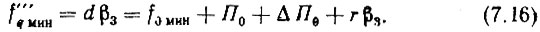
Остальные опорные частоты декады

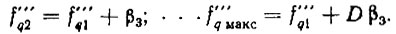
Приравняем значения f_{0 мин} = f₀₁ из (7.14) и (7.16). Тогда

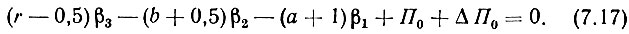
Так как условие f_{II мин} = П₀ + ΔП₀ + sβ₂ остается в силе и для этого варианта, то, будучи преобразованным и подставленным в (7.17), оно дает

Далее, рассуждая, как и раньше, получим

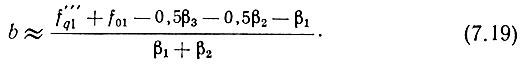
Затем, округляя b до целого значения, будем иметь

Остальные опорные частоты этой декады

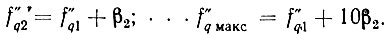
Наконец, из (7.14)

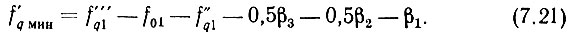
Остальные опорные частоты декады единиц

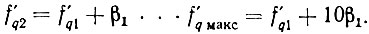
Опорные промежуточные и вторые промежуточные частоты декад в соответствии с (4.36) будут равны

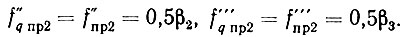
Диапазон частот ГУН декады сотен равен диапазону выходных частот системы, т. е. f_{0 мин} ÷ f_{0 макс}, а частотный диапазон ГУН декады десятков

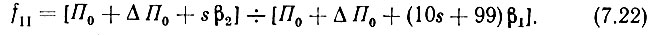
Первые промежуточные частоты декад лежат в пределах:

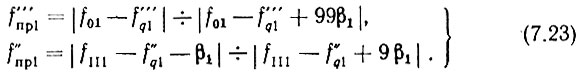
5. Расчет обеспечения выходной мощности, ее равномерности по диапазону и необходимого КБВ нагрузки.

Так как нами рассматривается система с автоподстраиваемым генератором в выходной декаде, то обеспечение требуемых значений выходной мощности и равномерности последней по диапазону обеспечивается соответствующей разработкой этого генератора (при этом необходимо учитывать отбор мощности гетеродинирующих колебаний P_г1 на первый смеситель). При отработке ГУН по указанным параметрам необходимо также обеспечить ширину зоны электронной настройки не уже 2 ΔF_уд ≥ 2Δf₀ при механической перестройке ГУН по диапазону или не менее П₀ + 2ΔF_уд = f_{0 макс} - f_{0 мин} + 2ΔF_уд при электрической перестройке.

Что же касается КБВ нагрузки, то из-за сложности расчета этого параметра последний должен определяться экспериментально. Для этого на круговой диаграмме Вольперта строятся нагрузочные характеристики ГУН и по ним определяется такое значение КБВ, при котором максимальное отклонение частоты не превосходит допустимой величины.

Однако снятие нагрузочных характеристик является весьма трудоемким процессом. Поэтому измерения можно упростить следующим образом. Собирается измерительная установка по структурной схеме рис. 7.2, ГУН через направленный ответвитель НО нагружен на переменный аттенюатор Ат переменный фазовращатель ФВр и короткозамыкающую нагрузку КЗ. Частота генератора контролируется счетчиковым частотомером СЧ. Изменением аттенюации добиваются такого минимального затухания Н_мин, при котором изменение фазы отраженной от КЗ волны в пределах 2π не вызывает отклонения частоты ГУН более нормы Δf_ГУН/Н. Нетрудно вычислить, что Н_мин эквивалентно нагрузке с КБВ_мин = (Н_мин - 1)/(Н_мин + 1). Если реальная нагрузка имеет КБВ_Н < КВН_мин, то нужно включить на выходе синтезатора аттенюатор с затуханием

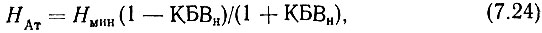
либо ферритовый вентиль с обратным затуханием, равным Н²_АТ (прямым затуханием пренебрегаем).

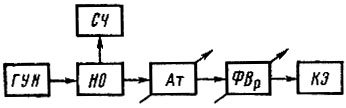
Рис. 7.2. Структурная схема установки для измерения влияния КБВ нагрузки на нестабильность частоты генератора

В случае включения аттенюатора мощность ГУН нужно увеличить в Н_АТ раз, т. е.

6. Расчет распределения уровней колебаний.

На основании выводов из практики задаемся:

- мощности колебаний опорных частот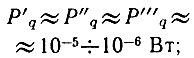

- напряжения колебаний опорных промежуточных и промежуточных частот, подаваемые на фазовые дискриминаторы,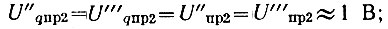

- коэффициенты передачи перестраиваемых фильтров в полосе прозрачности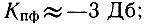

- коэффициенты передачи диодных балансных смесителей

Мощность автоподстраиваемого генератора выходной декады уже определилась выше (7.25). Переходное затухание направленного ответвителя, через который эта мощность подается на первый смеситель декады

Мощность ГУН декады десятков должна быть выбрана такой величины, чтобы с учетом переходных затуханий направленных ответвителей, включенных между этим ГУН и гетеродинным входом второго смесителя декады сотен G'''_HO2 и между ГУН и гетеродинным входом первого смесителя декады десятков G"_НО1, на указанные смесители подавалась необходимая мощность

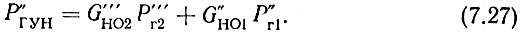
Выходная мощность декады единиц, если она подается в качестве мощности гетеродинирующих колебаний на второй смеситель декады десятков, должна быть порядка 1÷2 мВт, т. е. коэффициент усиления усилителя, включенного после фильтра, должен быть порядка 20÷30 дБ. Если же колебания декады единиц являются для второго смесителя декады десятков "сигнальными", то усилитель после ПФ не включается.

Для того чтобы режимы первых смесителей декад не зависели от мощности гетеродинирующих колебаний, поступающих на вторые смесители декад, при отсутствии первых УПЧ в декадах развязка между входами вторых смесителей должна быть не менее 10÷20 дБ.

Суммарные коэффициенты усиления УПЧ в кольцах ФАПЧ определяются из условия

Если в кольце применен один УПЧ, то значение К_УПЧ из (7.28) относится к его коэффициенту усиления, а если - два, то это значение распределяется между ними. При этом выходное напряжение первого УПЧ U_пр1 не должно превосходить значения, определяемого из выражения

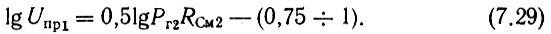
В некоторых случаях бывает целесообразно с точки зрения получения минимальных "полосовых" побочных составляющих на входах второго смесителя мощности "сигнала" и гетеродина поменять местами (в рассматриваемой нами схеме это целесообразно сделать на входах См₂ декады десятков). Тогда с выхода УПЧ₁ должна сниматься мощность Р_г2, а на "сигнальный" вход См₂ подаваться напряжение, не превышающее значения, полученного из (7.29). Напомним, что (7.29) выведено из условия, сформулированного в § 4.2, о необходимости иметь превышение мощности гетеродина над мощностью "сигнала" не менее 15 дБ (в последнем выражении приняты пределы 15÷20 дБ).

В реальных устройствах величины, входящие в знаменатель выражения (7.28), да и само значение К_УПЧ меняются при изменении частоты, смене полупроводниковых приборов, при изменении питающих напряжений, под влиянием климатических и механических воздействий и т. п. При этом, однако, значение U_пр2 должно оставаться примерно постоянным. Для этого в УПЧ вводятся системы АРУ и РРУ, необходимые коэффициенты регулирования которых можно определить, исходя из следующих соображений.

Следует различать "статические и "динамические" нестабильности коэффициентов передачи кольца от входа ПФ до входа ФД. "Статические" нестабильности это нестабильности, вызванные разбросом параметров деталей, входящих в элементы кольца и дающие изменения коэффициентов передачи при нормальных условиях. "Динамические" нестабильности вызываются изменением коэффициентов передачи элементов кольца при изменении частоты (по диапазону), климатических воздействий, питающих напряжений и т. п.

Учитывая это, сначала определяется максимально необходимый коэффициент усиления УПЧ К_{УПЧ макс макс} из (7.28) при подстановке в это выражение минимально возможных значений величин, взятых из технических условий (ТУ) на элементы кольца. Затем определяются из практики (или берутся из ТУ) "статические" нестабильности входящих в знаменатель (7.28) величин, добавляются к каждой величине (например, К_{ПФ мин} + ΔК'_ПФ) и определяется коэффициент усиления УПЧ К_{УПЧ макс}.

Коэффициент регулирования ручной регулировки усиления находим как

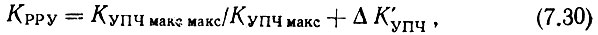
где ΔК'_УПЧ - "статическая" нестабильность коэффициента усиления УПЧ.

Для определения коэффициента регулирования АРУ поступает следующим образом. Задаемся допустимым значением увеличения крутизны ФД и определяем, таким образом, допустимую нестабильность выходного напряжения второго УПЧ ΔU_пр2 (напомним, что изменение U_пр2 влечет за собой такое же изменение крутизны ФД). Затем подставляем в числитель (7.28) значение U_пр2 + ΔU_пр2, а в знаменатель - максимально возможные при эксплуатации значения входящих величин; находим К_{УПЧ мин}.

Определяем коэффициент регулирования АРУ

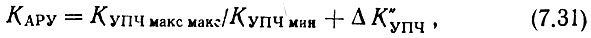
где ΔК"_УПЧ - "динамическая" нестабильность коэффициента усиления УПЧ.

Заметим, что в указанных целях применять в УПЧ ограничитель или использовать эффект насыщения транзистора недопустимо, так как при этом уменьшается коэффициент гармоничности напряжения.

Естественно, что при проектировании самого УПЧ необходимо ориентироваться на значение К_{УПЧ макс макс} и учитывать запасы на нестабильности этого коэффициента ΔК'_УПЧ и ΔК"_УПЧ.

Для дальнейших расчетов потребуется задаться полосами удержания ΔF_уд и захвата ΔF_з кольца ФАПЧ.

Полоса удержания ФАПЧ должна быть не меньше арифметической суммы неточности установки частоты ГУН Δf_уст нестабильности его частоты под действием всех дестабилизирующих факторов Δf_ГУН и нестабильности его частоты за счет нестабильного воздействия на ГУН цепи управления (нарушение симметрии ФД, уход нуля УПТ) - Δf_УПР. Кроме того, задавшись допустимым подчеркиванием низкочастотных помех системой ФАПЧ, из графика рис. 5.5 определяем необходимое расширение полосы удержания (при подчеркивании, равном 3÷4 дБ, полосу удержания необходимо расширить на 30÷40%):

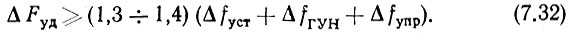
Полоса захвата ФАПЧ определяется из (5.34) и при υ ≈ 100 практически получается на порядок уже полосы удержания. Это значение уточняется после расчета кольца ФАПЧ.

Полоса пропускания УПЧ₂ известна из (4.31), а полоса пропускания УПЧ₁ должна быть не меньше шага дискретности опорных частот, поступающих на данную декаду:

Коэффициент усиления УПТ определяется, исходя из следующего условия. Если краю полосы удержания соответствует выходное напряжение фазового дискриминатора Е_уд, то

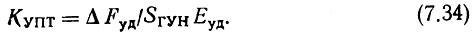
Полоса пропускания УПТ определяется при расчете кольца ФАПЧ.

Так как рассчитывается система ЧФАПЧ, то статизм ЧАП должен быть меньше полосы захвата ФАПЧ. Он равен

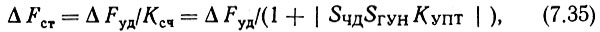
где К_сч - коэффициент стабилизации системы ЧАП; S_ЧД - крутизна характеристики частотного дискриминатора.

Если задаться ΔF_ст ≈ 0,25 ΔF_з и учесть (5.34), то из (7.35) можно получить

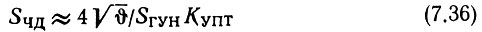
(уточняется после расчета кольца ФАПЧ).

При расчете частотного дискриминатора кроме S_ЧД необходимо учесть, что частота настройки должна быть равна f_{q пр2}, погрешность этой частоты не должна превышать 2ΔF_ст ≈ 0,5 ΔF_з и полоса захвата ЧАП должна быть

Полоса пропускания ФНЧ в кольце ЧАП (постоянная времени ФНЧ) должна быть рассчитана так, чтобы суммарное время окончания переходных процессов в кольцах ЧАП и ФАПЧ было бы значительно меньше заданного времени перехода на резерв Т_р.

7. Расчет параметров колец ФАПЧ

Вначале наметим порядок расчета кольца ФАПЧ старшей (выходной) декады синтезатора.

а. Для проведения расчета проектировщик должен располагать экспериментально снятой кривой частотного распределения энергетического спектра частотных шумов ГУН Υ_ГУНf = F(F_M) (рис. 7.3).

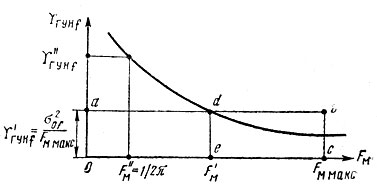
Рис. 7.3. К расчету необходимой полосы пропускания кольца ФАПЧ

Так как заданной является величина σ_0f в полосе частот с максимальной частотой F_{М макс}, то соответствующий этой девиации энергетический спектр частотного шума при равномерном распределении

Если провести прямую, параллельную оси абсцисс с ординатой Υ'_ГУНf, то получившийся прямоугольник O abc, ограниченный абсциссой F_{M макс}, будет иметь площадь, соответствующую заданной дисперсии частотных шумов σ²_0f. Обозначим абсциссу точки пересечения d через F'_M.

Если ограничить полосу пропускания кольца ФАПЧ частотой F'_M и обеспечить, чтобы в этой полосе сумма мощностей компенсированного шума ГУН и шума колебаний опорных частот отображалась прямоугольником О ade, а в полосе F_{M макс}-E'_M шум ГУН не компенсировался, но и шум колебаний опорных частот через кольцо ФАПЧ не проходил, то заданная шумовая характеристика будет обеспечена даже с некоторым запасом.

Так как в полосе пропускания ФАПЧ дисперсия шума не должна превосходить величины Υ'_ГУНfF'_M = σ²_0f(F'_M/F_{M макс}), то соответствующая ей шумовая девиация частоты

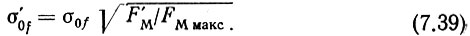
Для того чтобы составляющей собственных шумов в полосе пропускания ФАПЧ можно было пренебречь, зададимся величиной компенсированной шумовой девиации ГУН, не превышающей 0,01 от величины шумовой девиации σ'_0f.

Если измерить энергетический спектр шума ГУН Υ"_ГУНf на частоте F"_M = 1/2π (т. е. при Ω"_M = 1) и посчитать, что некомпенсированная мощность собственных шумов ГУН в полосе пропускания ФАПЧ равна Υ"_ГУНfF'_М, то можно определить коэффициент передачи замкнутого кольца ФАПЧ по ошибке V_θ(ω), необходимый для компенсации шумов ГУН:

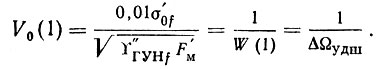
Откуда

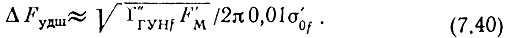
Сравнив значения ΔF_уд и ΔF_удш соответственно полученные из (7.32) и (7.40), выбираем большее и используем его в дальнейших расчетах.

Заметим, что значение усиления в кольце ФАПЧ, соответствующее величине полосы удержания, полученной из (7.40) для частоты F"_М, оказывается достаточным и во всей полосе пропускания ФАПЧ, так как, хотя с ростом частоты F_M коэффициент усиления уменьшается, но и интенсивность частотных шумов ГУН также падает примерно по тому же закону.

б. Задаемся полосой пропускания ФАПЧ

и из (5.11) определяем максимальное значение отношения постоянных времени пропорционально-интегрирующего ФНЧ:

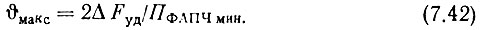
в. Задавшись коэффициентом затухания кольца ζ = 1, по графику рис. 5.3 определяем величину [ω_p(t)]. Из выражения (5.32) находим

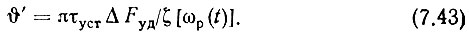
Сравниваем величины Ф, полученные из (7.42) и (7.43). Если υ' > υ_макс, то увеличиваем затухание ζ и, следовательно, [ω_pt] до тех пор, пока не наступит равенство υ' = υ_макс. Так как при этом остается 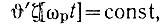то ни полоса удержания кольца, ни время установления синхронизма не изменятся. Однако обычно к этому приему прибегать не приходится хотя бы потому, что τ_уст всегда можно выбрать меньше заданного. Поэтому считаем, что всегда υ' < υ_макс.

Из (5.29) определяем меньшую постоянную времени ФНЧ

и из (5.17) - соответствующую ей круговую частоту Ω₂.

Находим по (5.30) резонансную частоту кольца ω_р, а по (5.31) и рис. 5.2 - время установления синхронизма

г. Из (5.26) определяем большую постоянную времени ФНЧ

и из (5.17) - соответствующую ей круговую частоту Ω₁.

д. Из (5.34) определяем полосу захвата ΔF_з.

е. Строим ЛАЧХ разомкнутого кольца (рис. 7.4), для чего:

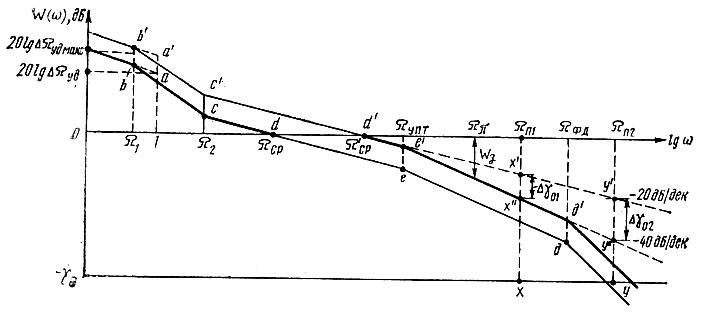
Рис. 7.4. Вид ЛАЧХ разомкнутого кольца ФАПЧ при учете изменения коэффициента усиления

- наносим на ось абсцисс с делениями в логарифмическом масштабе частоты ω = Ω₁, ω = Ω₂ и ω = 1;

- из точки (1; 0) восстанавливаем перпендикуляр 20 lgΔΩ_уд = 20 lg (2πΔF_уд), и через точку а на участке ω ≈ 0÷ω = Ω₁ проводим прямую с наклоном - 20 дБ/дек;

- на участке ω = Ω₁÷ω = Ω₂ из точки b проводим прямую bс с наклоном - 40 дБ/дек;

- из точки с проводим прямую cd с наклоном - 20 дБ/дек до пересечения с осью абсцисс; находим значение частоты среза системы Ω_ср;

- проверяем, чтобы

- выбираем частоту Ω_УПТ ≥ 4Ω_ср, обозначим ее на графике и продолжаем прямую cd до точки е с абсциссой Ω_УПТ;

- находим постоянную времени УПТ, определяющую его полосу пропускания:

- выбираем частоту Ω_ФД ≈ (50÷100)Ω_УПТ, наносим ее на график и проводим прямую eg с наклоном - 40 дБ/дек;

- определяем постоянную времени нагрузки ФД

- проводим из точки g в сторону увеличения частоты прямую с наклоном - 60 дБ/дек.

ж. Учитываем возможные изменения параметров выходного напряжения ФД (Е_уд + ΔЕ_уд), крутизны ГУН (S_ГУН + ΔS_ГУН) и коэффициента усиления УПТ (К_УПТ + ΔК_УПТ) и из (7.34) определяем максимально возможную во время эксплуатации полосу удержания ФАПЧ

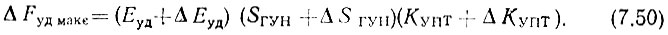
По правилам, изложенным в предыдущем пункте, строим вторую ЛАЧХ системы. Она пойдет выше первой и параллельно ей, так как нестабильностями собственных частот звеньев пренебрегаем (они косвенно учитываются запасами по фазе и усилению).

Находим Ω'_ср и проверяем Ω'_ср < Ω_УПТ.

з. Учитывая, что при ω > Ω_ср W₀₁(ω) ≈ W(ω), определяем степень подавления побочных составляющих кольцом ФАПЧ, для чего:

- проводим прямую (-γ₀, дБ) до значений ω, соответствующих частотам помех Ω_п1, Ω_п2, ... (точки х, у, ...);

- продолжаем прямую c'd' (наклон - 20 дБ/дек) до точек x', y', ...;

- так как ординаты точек x', y', ... учитывают степень подавления побочных составляющих кольцом ФАПЧ без действия УПТ (только интегратором кольца и пропорционально-интегрирующим фильтром), а ординаты точек х", у", ... - также и УПТ, то, пренебрегая влиянием на фильтрацию нагрузки ФД (оно может служить определенным запасом расчета), определяем вклад УПТ в подавление побочных составляющих в виде добавок Δγ₀₁, Δγ₀₂,... в дБ.

Заметим, что подавление побочных составляющих, равное разности ординат (х-х"), (у-у"), ..., должно обеспечиваться в цепях формирования колебаний опорных частот кольца ФАПЧ. Поэтому обычно корректирующих звеньев можно в кольцо ФАПЧ не включать.

и. Определяем устойчивость системы по фазе. Для этого нужно построить ЛФЧХ по выражению (5.37), задаться запасом по фазе θ_З ≈ 30÷45°, затем найти фазовый сдвиг, вносимый трактом усиления промежуточной частоты Δθ_ПЧ, а по нему из (5.12) определить крутизну S_θПЧ. Однако этот расчет слишком громоздок и не оправдывает получаемую с его помощью точность.

Имея в виду минимально-фазовый характер примененных в кольце ФАПЧ звеньев, воспользуемся приближенной ф-лой (5.46) и определим по ней необходимую крутизну фазовой характеристики тракта промежуточных частот, выбрав θ_з = 0,5÷0,8:

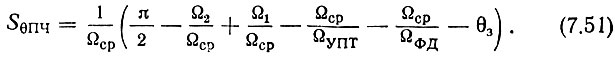
Расчет проводим для двух значений частоты среза: Ω_ср и Ω'_ср и из двух значений S_θПЧ выбираем меньшее.

Учитывая, что полоса пропускания тракта П_ПЧ = П'_ПЧ/n, а также малость Δθ_ПЧ, из (5.12) и (5.13) получаем полосу пропускания тракта промежуточных частот

к. Для определения запаса по усилению нужно найти частоту Ω_π, на которой фазовая характеристика разомкнутого кольца достигает значения -π. Так как мы условились не строить ЛФЧХ, то определим аналитически, предположив, что, как правило, 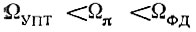и в этих пределах ЛФЧХ достаточно линейна.

Учитывая, что 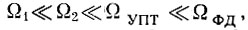, найдем значения фазовой характеристики на частотах Ω_УПТ и Ω_ФД:

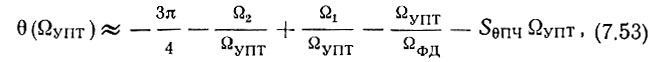
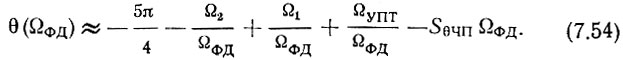
Из подобия треугольников (рис. 7.5) можно записать

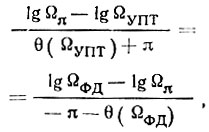
откуда после несложных преобразований получим

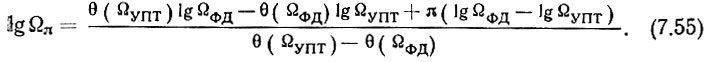
Определив из (7.55) значение Ω_π и отложив его на ЛАЧХ, определим запас по усилению (по амплитуде) W_з ≥ 10 дБ.

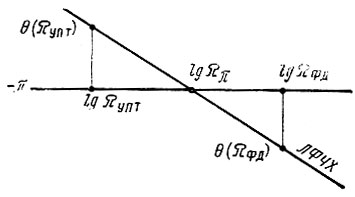
Рис. 7.5. К расчету частоты Ω_π

л. Определяем максимальную скорость поиска (при поиске ЧАП выключена, чтобы не расходовать полосу удержания ФАПЧ). Для этого из рис. 5.4 по известному ζ определяем значение относительного выброса фазы υ. Затем находим среднеквадратичное значение фазовых флуктуаций. По аналогии с (6.13) можно записать σ_0φ =2πσ_0f/τ_с и τ_с = 1/2 П_ФАПЧ, т. е.

Подставляя (7.56) в (5.35), получим (в Гц/с)

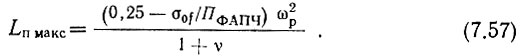
Расчет второго кольца ФАПЧ синтезатора производится по той же методике, что и кольца выходной декады.

8. Расчет обеспечения коэффициентов гармоничности.

Как отмечалось в гл. 4, для предотвращения "зеркальной настройки" на соседнюю опорную частоту ПФ всех декад, в которых применена ФАПЧ, должна подавлять колебания гармоник, соседних с фильтруемой, на

Находим коэффициенты гармоничности выходных колебаний всех декад, кроме выходной.

Для декады десятков, содержащей кольца ФАПЧ, из (4.69) с учетом фильтрующего действия УПТ

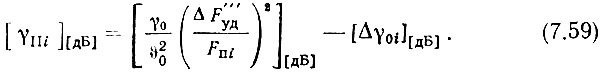
Если смесители линейные и безынерционные, то для декады единиц, в которой используется пассивная фильтрация, из (4.62)

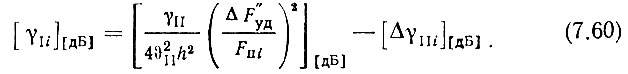
В последнем случае, если линейность или безынерционность смесителей нельзя получить или хотя бы гарантировать,

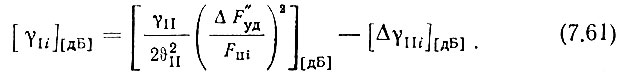
В выражения (7.59)-(7.61), а также в (7.62) и (7.63) следует подставлять все значения F_п, которые встречаются в данной и предыдущей декадах.

Используя выражения (4.73) и (4.75) с учетом (4.63). определяем коэффициенты гармоничности выходных колебаний декад по "полосным" побочным составляющим.

Определяем необходимые коэффициенты гармоничности напряжений опорных частот декад по входам фазовых дискриминаторов. Так как на балансный фазовый дискриминатор подаются оба напряжения равных амплитуд и, принимая коэффициент передачи дискриминатора равным единице, из (4.40) и (4.45) получим

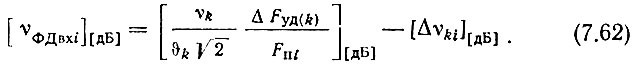
Находим необходимые значения коэффициентов гармоничности колебаний опорных частот, поступающих с МОЧ, в предположении, что входным фильтром декады подавляются только составляющие основной сетки частот

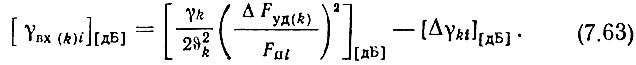
Если из последнего выражения γ_вх(k) получается более 300, то проверка по (4.72) не имеет смысла.

9. Расчет шумовых характеристик.

Выше (см. § 7.1) указывалось, что шумовая характеристика на выходе системы обычно задается в виде одного из трех параметров: σ_0f, σ_0φ или δσ_0f. Для удобства пользования при расчете выведенными выше выражениями приведем эти параметры к одному среднеквадратичному значению шумовой девиации частоты σ_0f (или к дисперсии частотных шумов σ²_0f).

Если задана σ_0φ, то по аналогии с (6.13) будем иметь

в полосе пропускания

если задана δσ_0f, то

Так как полоса пропускания кольца ФАПЧ обычно выбирается не меньше полосы частот, в которой задается шумовая характеристика системы, то должно быть выполнено неравенство (4.119).

Из (4.103) находим коэффициент шума линейной части устройства для разомкнутого кольца ФАПЧ:

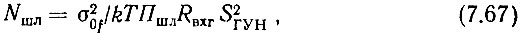
где

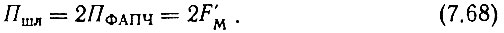
Найдем значения параметров, входящих в выражение. (4.116).

Шумовой параметр смесительного диода Ш_Д находим из рис. 4.8, задавшись параметрами диода а ≈ (15÷25) 1/В, ρ_д ≈ 5⋅10^-7÷5⋅10^-3 (меньшие значения имеют кремниевые, а большие - германиевые диоды) и определив амплитуду напряжения

Параметр χ для первого смесителя находим как отношение

Задавшись N'_{ш См1} ≈ 8÷10, из выражения (4.116) находим коэффициент Λ.

Задавшись N_{ш УПЧ} ≈ 3÷10, из (4.115) определим коэффициент шума на выходе генератора гармоник старшей декады N'''_шq при разомкнутом кольце ФАПЧ в случае одного УПЧ₂ в декаде, а в случае двух УПЧ в декаде

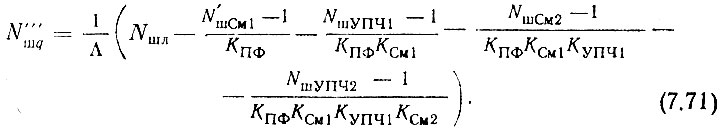
Далее по изложенному выше плану можно было бы рассчитать шумовые характеристики декад десятков и единиц, а также оставшихся ГОЧ и генераторов гармоник. Однако этого делать нет никакой необходимости, исходя из следующих соображений. Требования к декаде десятков значительно менее жесткие, чем к выходной декаде, что видно из сравнения (4.110) и (4.111). В связи с идентичностью построения схем декад сотен и десятков, требования к декаде единиц оказываются еще менее жесткими, чем к декаде десятков. Кроме того, так как в МОЧ имеется один общий ЭЧ, то коэффициент умножения частоты в той части МОЧ, которая работает на выходную декаду, оказывается наибольшим и, следовательно, ее шумовые характеристики - наихудшими. Поэтому, если удастся так выполнить наиболее высокочастотную (выходную) декаду, чтобы ее шумовые характеристики удовлетворяли заданным, то шумовые характеристики остальной части схемы обязательно окажутся достаточно хорошими.

Пользуясь выражением (4.122), определим шумовую девиацию частоты колебаний на выходе генератора гармоник выходной декады при замкнутом кольце ФАПЧ:

10. Расчет системы генераторов гармоник производится на основании требований, сформулированных в процессе расчета синтезатора: количество генераторов гармоник; диапазон частот; число Опорных частот α; шаг дискретности опорных частот β; выходная мощность P_q; неравномерность выходной мощности ΔP_q; коэффициенты гармоничности выходных колебаний γ_gm; шумовая девиация частоты σ_qf.

Количество генераторов гармоник в системе, очевидно, должно соответствовать числу декад устройства k.

Частотные диапазоны генераторов гармоник, число опорных частот и шаг дискретности опорных частот определяются вычисленными значениями по выражениям (7.5)-(7.8).

В соответствии с п. 6 расчета минимальные выходные мощности генераторов гармоник, как правило, принимаются P_q ≈ 10^-6 Вт. Неравномерность выходной мощности (при большем перекрытии диапазона частот) обычно берется порядка +10 дБ.

Из выражения (7.63) для всех F_п, действующих в системе (кроме F_п = f_{ГГ вх}), известны коэффициенты гармоничности колебаний опорных частот.

Наконец, из (7.72) известна шумовая девиация частоты на выходе генератора гармоник старшей декады.

Выходные параметры генераторов гармоник дают возможность определить входные параметры последних, т. е. выходные параметры тех ГОЧ, которые включены на входах генераторов гармоник. На основании изложенного в гл. 4 и 6 можно принять следующие положения при определении входных параметров генераторов гармоник: достигнутый к настоящему времени коэффициент передачи генераторов гармоник, генерирующих гармоники при m = 40÷60, определяется выражением (6.19); коэффициент гармоничности колебаний на выходе генератора гармоник уменьшается по сравнению со значением этого коэффициента на входе генератора гармоник пропорционально номеру гармоники; шумовая девиация частоты на выходе генератора гармоник увеличивается по сравнению с входной пропорционально номеру гармоники.

Таким образом, расчетные формулы для определения входных параметров генератора гармоник могут быть записаны следующим образом.

Входная мощность при учете выражения (6.19)

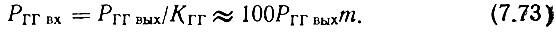
При этом амплитуда входного высокочастотного напряжения и напряжение смещения определяются примененным в генераторе гармоник диодом.

Коэффициенты гармоничности входных колебаний

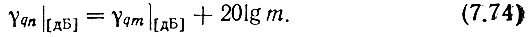
Шумовая девиация частоты на входе генератора гармоник

11. Расчет системы генераторов опорных частот производится на основании требований, сформулированных при расчете синтезатора и системы генераторов гармоник.

Система ГОЧ должна обеспечить подачу на входы генераторов гармоник и на фазовые дискриминаторы колебаний, характеризующихся следующими параметрами: частота, мощность и напряжение на генераторе гармоник или напряжение на входе фазового дискриминатора; коэффициенты гармоничности выходных колебаний; шумовая девиация частоты.

Значения всех этих параметров нами уже определены выше. Действительно, выходные частоты ГОЧ определены из выражений: (7.3)÷(7.9). Следовательно, число ГОЧ определяется суммой числа генераторов гармоник и фазовых дискриминаторов.

Мощности и напряжения, подаваемые на генераторы гармоник, определяются выражением (7.73) и типами примененных диодов. Напряжения, подаваемые на фазовые дискриминаторы, для большинства типов ФД определяются величиной порядка 1 В. Учитывая, что ГОЧ могут соединяться с нагрузками непосредственно или коаксиальными кабелями, а генераторы гармоник - либо волноводами, либо коаксиальными кабелями, необходимо перед расчетом системы ГОЧ решить вопрос о наиболее конструктивных и энергетически выгодных видах соединений. В некоторых случаях оказывается целесообразным расчленить ГОЧ так, что его выходной каскад располагается непосредственно у нагрузки и соединяется с остальным ГОЧ кабелем.

Коэффициенты гармоничности выходных колебаний ГОЧ определены выше выражениями (7.62), (7.63) и (7.74).

Возможности достижения необходимой степени гармоничности выходных колебаний ГОЧ существенным образом влияют на выбор структурной схемы системы ГОЧ, а также на выбор номинального значения частоты эталона частоты f_q0. Такой пример было рассмотрен в гл. 6. По соображениям, изложенным в гл. 6, целесообразно стремиться к выбору f_q0 = β₂ и к такому построению системы ГОЧ, при котором колебания каждой опорной частоты генерировались бы отдельным ГОЧ (последнее создает удобства при изготовлении и эксплуатации аппаратуры).

Шумовые характеристики всей системы ГОЧ определены выше выражением (7.75) для выходной декады.

12. Расчет эталона частоты (ЭЧ) производится на основании принципов, изложенных в гл. 6. Это наиболее ответственный элемент в составе всей системы ДКСЧ СВЧ диапазона, так как основные выходные параметры системы; погрешность частоты и ее кратковременная нестабильность (шумовые характеристики) полностью определяются ЭЧ.

Эталон частоты состоит из опорного кварцевого или квантового генератора, системы термостатирования, системы терморегулирования, системы контроля температуры и усилителя колебаний частоты f_q0. Для ограничения спектра шумов между кварцевым генератором и усилителем обычно включается узкополосный фильтр (УПФ). В отдельных случаях, котла частота кварцевого генератора и выходная частота ЭЧ находятся в кратном отношении, в состав ЭЧ входит умножитель или делитель частоты.

Кварцевый генератор должен быть рассчитан на генерирование колебаний частоты f_q0 с заданной погрешностью δf_q0. В составе ГКО должен быть буферный усилитель. Для достижения высокой стабильности частоты при изменении внешней температуры кварцевый резонатор, генератор и буферный усилитель следует термостатировать. Точность поддержания температуры в термостате рассчитывается по измеренному ТКЧ генератора. Как было показано в гл. 6, на температурную нестабильность целесообразно отводить не более 20% погрешности частоты.

Система терморегулирования СТР рассчитывается, исходя из необходимой точности поддержания температуры в термостате. Кроме того, ее мощность должна быть такой, чтобы номинальный температурный режим обеспечивался за время, отведенное для полной готовности аппаратуры к работе. Для этого, как правило, СТР включает в себя устройство форсированного прогрева.

Система контроля температуры предназначена для выполнения двух функций; для сигнализации и выключения подогрева термостата при аварийных отклонениях температуры от номинальной и для установки номинального значения температуры в условиях эксплуатации.

Дисперсия частотных шумов ЭЧ рассчитывается, исходя из требований к шумовым характеристикам колебаний опорных частот. Обычно наиболее критичным является требование к дисперсии шумов опорных частот на выходе генератора гармоник старшей декады (σ'''_qf)². Поэтому дисперсия частотных шумов эталона частоты

где m - максимальный коэффициент умножения генератора гармоник выходной декады; n - коэффициент умножения ГОЧ, включенного между ЭЧ и этим генератором гармоник.

Обычно получить нужную величину σ_q0f от ГКО не удается. Поэтому колебания ГКО фильтруются узкополосным фильтром УПФ, одним из способов, указанных в гл. 6.

Расчету должно предшествовать экспериментальное снятие частотного распределения энергетического спектра частотного шума в полосе, ограниченной частотой F'_M. Распределение в общем случае имеет довольно нерегулярный вид и зависит от большого числа различных факторов. Поэтому предъявление требований к УПФ является сложной и неоднозначной задачей. Однако попробуем хотя бы грубо представить себе порядок величин параметров УПФ. Для этого обратимся к рис. 7.6, на котором изображена характерная зависимость Υ_q0f(F_M). Аппроксимируем указанную кривую ломаной abc так, чтобы площади под кривой и под ломаной возможно больше совпадали. При этом найдем граничную частоту F_Mгр. Так как F_Mгр весьма мала, то подавить фильтром составляющие спектра в полосе частот ниже F_Mгр, как правило, не удается. Поэтому допустим, чтобы эти составляющие существовали на выходе ЭЧ.

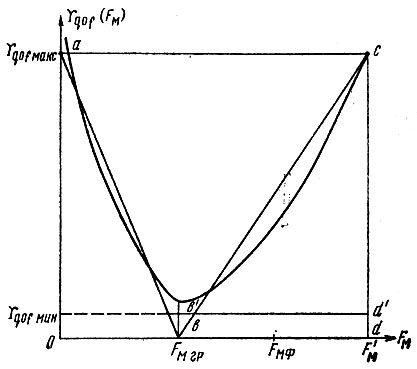
Рис. 7.6. К расчету УПФ эталона частоты

Из рис. 7.6 следует, что

где σ²_0ab и σ²_bcd - дисперсии частотных шумов при принятой аппроксимации в полосах частот 0÷F_Mгр и F_Mгр÷F'_M соответственно.

Из построения следует, что

и

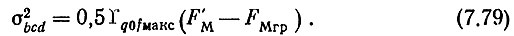
Если условиться, что

где

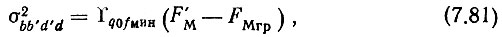
то, разделив (7.79) и (7.81), определим необходимую степень подавления фильтром шумов ГКО:

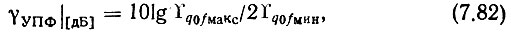
где из (7.78), (7.80) и (7.81)

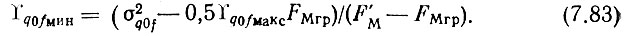
Таким образом, УПФ, включенный после ГКО, должен вносить затухание γ_УПФ, определяемое (7.82) на частоте, примерно равной

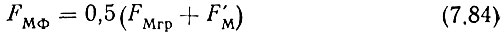
(учитывая монотонность характеристики затухания УПФ).

Полоса пропускания УПФ (по уровню -3 дБ), очевидно, должна быть не уже 2 f_q0δf_q0 плюс абсолютная погрешность настройки самого УПФ на частоту f_q0.

В некоторых случаях при малых фликкер-шумах ГКО и недостаточной разрешающей способности измерительной аппаратуры, снять левую восходящую ветвь кривой Υ_q0f(F_M) не удается, вследствие чего граничную частоту F_{M гр} определить оказывается довольно затруднительно. Выйти из создавшегося положения можно, воспользовавшись рекомендациями [176], где указывается, что при τ_с > 0,1 с основной вклад дают технические шумы ГКО, а при τ_с < 0,1 с - дробовые шумы. Так как τ_с = 0,1 с соответствует F_M = 5 Гц, то в ф-лы (7.83) и (7.84) для рассматриваемого случая можно подставить F_{M гр} = 5 Гц. При этом, как правило, расчет дает запас.

13. Заданная степень надежности достигается обычными мерами обеспечения надежности радиоустройств (максимальным применением полупроводниковых приборов и интегральных микросхем, исключением механических и электромеханических систем перестройки и коммутации, облегчением электрических и тепловых режимов элементов, соблюдением технологии изготовления и т. д.) и резервированием блоков с автоматическим выключением отказавшего и включением резервного при наличии сигнализации об этом.

Приведем расчетные выражения, характеризующие надежность системы из двух блоков: основного и резервного, находящегося в состоянии теплого резерва.

Так как после расчета принципиальной схемы блока оказывается известной его суммарная лямда-характеристика λ_Σ, то, как известно, среднее время наработки блока на один отказ

Среднее время наработки на отказ системы из двух одинаковых блоков

Вероятность безотказной работы системы из двух одинаковых блоков в течение заданного времени t может быть приблизительно определена

где время t обычно считают временем необслуживаемой работы станции.