7.3. Методика инженерного расчета системы ДКСЧ с цифровым синтезатором

Перед началом расчета считаем заданными основные параметры системы ДКСЧ и выбранными структурную схему синтезатора в соответствии с рис. 3.2 с двумя опорными частотами f'_q и структурную схему МОЧ (см. гл. 6). Основываемся также на том, что применен ДПКД с прямым переносом импульса выборки, фазовый дискриминатор типа "выборка-запоминание" и пропорционально-интегрирующий ФНЧ.

1. Выбор частотного плана производим так же, как и для случая применения активного многодекадного синтезатора (см. § 7.2, п. 1).

2. Число дискретных частот системы α'₀ находим при наличии защитного интервала Z_H и при односторонних расположениях частот, а также при Z₀ и двустороннем внешнем расположении частот по (7.1), а при двустороннем внутреннем расположении или при Z_H = 0 - как α'₀ = α₀ (α₀ - заданное количество частот).

3. Число десятичных разрядов в цифровом изображении

Характеристика логарифма показывает число полных разрядов, а ненулевая мантисса указывает на наличие еще одного неполного разряда, самого старшего.

4. Расчет частотообразования и коэффициентов деления

Определим шаг дискретности опорных частот. При k разрядах

Из (4.77) определяем шаг дискретности β₁. Полосы пропускания УПЧ П_УПЧ1 и П_УПЧ2 находятся из (4.78). Предварительно выбираем значения второй промежуточной частоты из условия непропускания УПЧ₂ частоты β₁:

Это условие объясняется следующим образом. В систему перед генераторами гармоник включены достаточно мощные ГОЧ(β₁) и ГОЧ(β₂), наводки от которых могут попасть на вход УПЧ₂ и вызвать паразитные колебания на входе ДПЧ. Так как одновременно должны выполняться соотношения (4.77) и (4.78), то совсем избежать наводок, очевидно, нельзя. Однако если f_{пр2 макс} > β₂, то в полосу пропускания УПЧ₂ попадает и частота β₂ и вторая гармоника частоты β₁, а если выполнить условие (7.90), то возникает опасность попадания только частоты β₁, т. е. требования к экранировке облегчаются.

Следует остановиться на одном важном вопросе, специфичном для систем с цифровыми синтезаторами СВЧ. Так как синтезаторы, в том числе и цифровые, являются декадными, то каждый переключатель набора номеров фиксированных частот должен соответствовать определенному десятичному разряду числа, выражающего номер фиксированной частоты. В § 7.2 показано, что в многодекадных синтезаторах разряды переключались полосовыми фильтрами декад. При этом, благодаря независимому выбору номинальных значений частот декады единиц, выходная частота № 1 системы могло присваиваться любому номинальному значению f_0i. В цифровых синтезаторах это совсем не так. Здесь старший десятичный разряд переключается полосовым фильтром опорных частот f"_q, а остальные разряды - переключателями декад ДПКД.

Выше было обосновано требование уменьшения коэффициента деления ДПКД при увеличении f_0i, т. е. при увеличении номера фиксированной частоты. Для одновременного изменения цифры, выражающей разряд десятков в номере фиксированной частоты, и числа десятков коэффициента деления ДПКД значению второй промежуточной частоты, соответствующему первому номеру выходной частоты f₀₁, должен соответствовать коэффициент деления декады единиц ДПКД, равный восьми. Для трехразрядного синтезатора можно записать

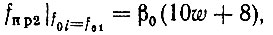
где w - коэффициент деления декады десятков ДПКД.

Однако для того, чтобы и опорные частоты f'_qi переключались согласно общей программе (каждый раз через пять переключений старшей декады ДПКД), переключатель этих частот с контактами, соединенными параллельно но пять штук в две группы, должен быть спарен с переключателем старшей декады ДПКД. При этом оказывается необходимым иметь максимальное значение второй промежуточной частоты на β₀ больше указанного выше значения, т. е.

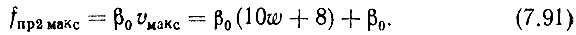
Эту величину будет иметь вторая промежуточная частота на 50, 100 и т. д. номерах фиксированных частот.

Так как β₂ = 2β₁ = 100 β₀, то можно показать, что фиксированная частота № 1 на выходе системы должна иметь такое номинальное значение, при котором цифра младшего разряда была бы равна 2β₀. Например, при β₀ = 1 МГц - f₀₁ = 3782 МГц; при β₀ = 2 МГц - f₀₁ = 3784 МГц и т. д.

Поэтому выбор f_{пр2 макс} по (7.90) следует производить сразу с учетом (7.91). Легко показать, что если бы требовалось с увеличением f_0i увеличивать коэффициент деления ДПКД, то частота № 1 должна была иметь в младшем разряде цифру, равную β₀.

С другой стороны, даже если номинальное значение частоты f_0i и будет удовлетворять этому требованию, то может оказаться, что номинальное значение f_{пр2 макс} окажется весьма неудобным для практического осуществления системы (либо слишком малым, либо слишком большим, хотя и оканчивающимся цифрой 8). Поэтому обычно следует поступать так: выбирать f_{пр2 макс} оптимальной с точки зрения проектирования синтезатора с соблюдением (7.91), а частоту № 1 относить вниз за пределы назначенного техническим заданием частотного диапазона. При этом рабочий диапазон будет начинаться с фиксированной частоты более высокого номера, но логическая связь декадных переключений будет выдержана, что особенно важно для упрощения автоматической перестройки и дистанционного управления.

Вначале рассмотрим расчет при варианте расположения частот 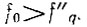Для этого варианта должно выполняться условие (4.79), Т. е. f'_q > f_пр1.

При этих исходных данных основное уравнение частотного плана запишется следующим образом:

Если частота № 1 обозначается на табло как "001", то в соответствии с (7.91) и (7.92)

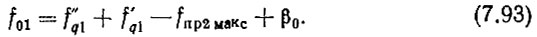
Так как сетки опорных частот являются гармониками опорных частот, поступающих на генераторы гармоник, f'_q1 = b β₁ и f"_q1 = dβ₂, то (7.93) можно записать как

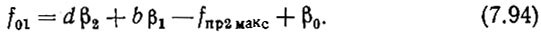
По условию (2.44) f"_{q макс} < f_{0 мин} - ΔП₀ или, превратив это неравенство в равенство,

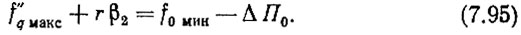
Можно представить D = α₀/β₂ (в случае дроби D округляется увеличением до целого числа).

С учетом последнего (7.95) запишется

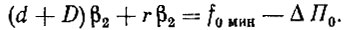
Откуда

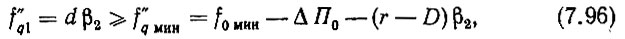
где r выбирается в соответствии с селективностью полосового фильтра. Округляем получившееся значение f"_q1 увеличением до целого значения, кратного β₂.

Остальные опорные частоты старшего разряда

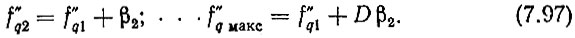
Если в (7.93) вместо f₀₁ подставить f_{0 макс}, то можно записать

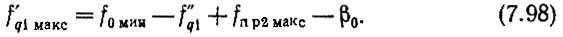
Если полученное из (7.98) значение f'_{q1 макс} округлить в сторону уменьшения до величины, кратной β₁, а затем подставить получившуюся величину f'_q1 в (7.93), то найдем фиктивную частоту f₀₁ системы, имеющую № 1. Реальная минимальная частота f_{0 мин} будет, очевидно, иметь номер

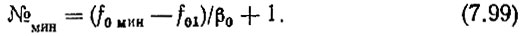
Заметим, что при таком расчете автоматически выполняется условие (2.29)

Далее находим вторые значения определенных выше частот

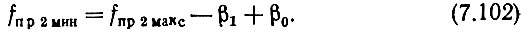
Рассмотрим второй вариант, когда f₀ < f"_q. Для этого варианта должно выполняться условие (4.80): f'q < f_пр1.

При отмеченных исходных данных основное уравнение частотного плана запишется как

Если частота № 1 обозначается на табло как "001", то в соответствии с (7.91) и (7.103)

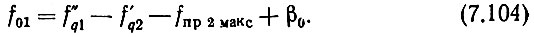
Но, как и ранее, 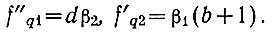Поэтому можно записать (7.104) в виде

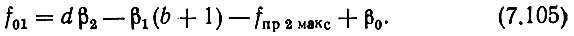
Для рассматриваемого варианта согласно второму условию (2.44) f"_{q мин} > f_{0 макс} + ΔП₀ или в виде равенства

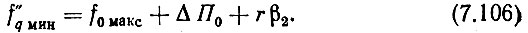
Но f_{0 макс} = f_{0 мин} + П₀. С учетом этого (7.106) запишется:

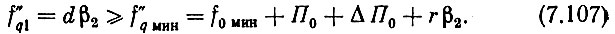
Округляем получившееся значение f"_q1 увеличением до целого значения, кратного β₂.

Остальные опорные частоты старшего разряда

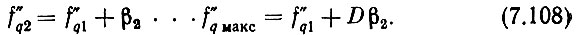
Если в (7.104) подставить f_{0 мин} вместо f₀₁, то можно записать

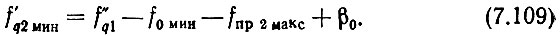
Если полученное из (7.109) значение f'_q2мин округлить в сторону увеличения до значения, кратного а затем подставить получившуюся величину f'_q2 в (7.104), то найдем фиктивную частоту f₀₁ системы, имеющую № 1. Реальная минимальная частота f_{0 мин} будет иметь номер, определяющийся выражением (7.99).

Минимальное значение второй промежуточной частоты определяется по-прежнему из (7.102), а

Как очевидно, и в этом случае неравенство (7.100) выполняется.

Пределы изменения первой промежуточной частоты для обоих вариантов найдем из выражения

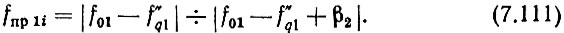
При необходимости для системы с цифровым синтезатором можно построить частотный план, аналогичный плану рис. 7.1.

Зная реально выполнимое быстродействие ДПКД f_{ДП макс}, определяем минимально возможное значение коэффициента деления ДФКД

Для обеспечения надежности работы ДФКД последний следует проектировать в виде последовательной цепочки триггеров с двумя устойчивыми состояниями. Поэтому полученную из (7.112) величину с округляем в сторону увеличения до ближайшего значения члена геометрической прогрессии со знаменателем, равным двум, т. е. до значений 1, 2, 4, 8, 16 и т. д.

Из (3.15) находим величину опорной частоты, подаваемой на фазовый дискриминатор, f_{q пр3}.

Наконец, рассчитаем коэффициенты деления частот в ДПКД

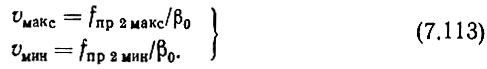
5. Расчет обеспечения выходной мощности, ее неравномерности по диапазону и необходимого КБВ нагрузки тождествен таковому для случая применения активного многодекадного синтезатора (см. § 7.2, п. 5).

6. Расчет распределения уровней колебаний. Изложенный в п. 6 § 7.2 расчет до пункта, включающего выражение (7.32), в части, относящейся к выходной декаде активного многодекадного синтезатора, можно целиком использовать и для случая цифрового синтезатора. При этом следует иметь в виду лишь следующие частности: амплитуда выходного напряжения УПЧ₂ U_mУПЧ2 должна быть взята, не превышающей допустимого для примененной на входе ДПЧ микросхемы уровня, а нагрузкой для УПЧ2 служит входное сопротивление этой микросхемы; амплитуда А_ИВ и длительность τ_ИВ импульсов выборки с выхода ДПЧ определяется конкретной схемой фазового дискриминатора и параметрами примененных в последнем элементов; хотя график рис. 5.5 предназначен для случая балансного фазового дискриминатора, а в нашем случае используется ФД типа "выборка-запоминание", при принятой нами синусоидальной форме напряжения опорной частоты, подаваемой на ФД, оба они имеют косинусоидальную характеристику, что дает право использования графиком и при расчете цифровых синтезаторов СВЧ; коэффициент усиления УПТ рассчитывается по ф-ле (7.34).

7. Расчет параметров кольца ЦФАПЧ

а. Пользуясь экспериментально определенным энергетическим спектром частотных шумов ГУН Υ_ГУНf(F_M) - рис. 7.3 (см. § 7.2, п. 7а), находим из (7.38) Υ'_ГУНf; из графика - частоту F'_М; из (7.39) - девиацию σ'_0f; из графика - значение Υ"_ГУНf, соответствующее частоте F"_M = 1/2π, и, наконец, из (7.40) - значение полосы удержания ΔF_удш, необходимое для компенсации шумов ГУН в полосе 0÷F'_M.

б. В соответствии с выражением (5.87) находим минимальное значение эквивалентной полосы удержания

Сравниваем ΔF_{удэ мин}, полученное из (7.114) с ΔF_удш, полученным из (7.40) и если ΔF_{удэ мин} < ΔF_удш, то из (7.114) находим новое значение ΔF_уд, которое соответствует ΔF_{уд мин} = ΔF_удш.

Если же при сравнении окажется, что ΔF_{уд мин} ≥ ΔF_удш, то оставляем величину ΔF_уд прежней.

Поскольку S_ФД и S_ГУН определены, то при увеличении ΔF_уд необходимо во столько же раз увеличить коэффициент усиления УПТ.

Далее можно было бы строить расчет по тому же плану, что и кольца аналоговой ФАПЧ многодекадного синтезатора. Однако следует помнить, что, во-первых, при неидеальном фиксирующем элементе помехи с частотой f_{q пр3} и ее гармоники в ФД полностью не подавляются (коэффициент неидеальности 1 > χ_ФД > 0); во-вторых, на входах ФД напряжения с частотой f_{q пр3} являются полезными и не могут быть подавлены до ФД и, в-третьих, процесс подавления помех кольцом ФАПЧ находится в противоречии с широкополосностью последнего, т. е., в конечном счете, с компенсацией собственных шумов ГУН, с увеличением полосы захвата и уменьшением времени установления синхронизма. Однако первейшим требованием все же является обеспечение нужного коэффициента гармоничности выходных колебаний. Поэтому вначале сформулируем требования к параметрам кольца по этой характеристике, а затем, как следствие, получим остальные его параметры.

в. Задаемся или измеряем коэффициент неидеальности ФД χ_ФД, определенный выражением (5.47), и рассчитываем необходимую степень подавления кольцом ЦФАПЧ помехи с частотой F_п1 = f_{q пр3}:

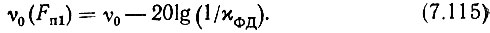
г. Учитываем возможные изменения параметров выходного напряжения ФД (Е_уд + ΔЕ_уд), крутизны ГУН (S_ГУН + ΔS_ГУН) и коэффициента усиления УПТ (К_УПТ + ΔК_УПТ) и из (7.50) определяем максимально возможную полосу удержания ЦФАПЧ ΔF_{уд макс}.

д. Найдем значение верхней частоты среза Ω'_{ср в}. Из материалов § 5.3 следует, что степень подавления помех по опорному входу ФД определяется смещенной ЛАЧХ разомкнутой системы, а из рис. 7.4 видно, что минимальное подавление получается, когда эта ЛАЧХ соответствует ΔF_{уд макс}. Для эффективного подавления помехи с частотой F_п1 = f_{q пр3} поместим частоту Ω_п1 = 2πF_п1 на участке, где ЛАЧХ имеет наклон -40 дБ/дек, для чего должно быть выбрано Ω_УПТ < Ω_п1.

Для расчета начертим примерный ход смещений ЛАЧХ при ΔF_{уд макс} (рис. 7.7). Из рис. 7.7 следует, что

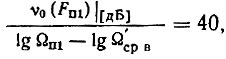
откуда

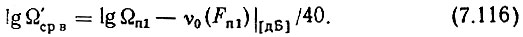
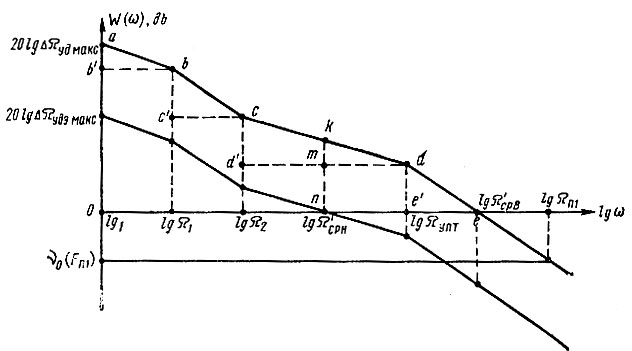
Рис. 7.7. К расчету полосы пропускания кольца ЦФАПЧ

Далее, из рис. 7.7.

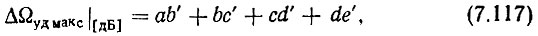
или, подставляя в правую часть (7.117) значения отрезков, будем иметь

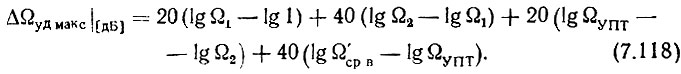
Из (7.118) получим

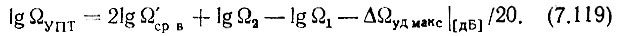
Легко проверить, что результат (7.119) справедлив и при Ω₁ < 1.

е. Рассчитаем полосу пропускания ЦФАПЧ. Для этого вначале определим минимальное отношение постоянных времени ФНЧ. Из (7.119)

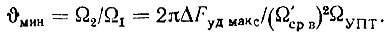
Но из рис. 7.7 следует, что

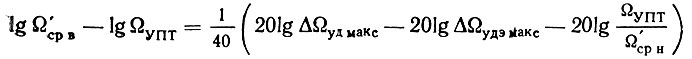
или

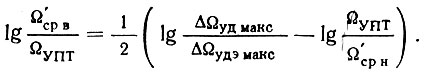
Так как ΔΩ_{уд макс}/ΔΩ_{удэ макс} = cυ_мин и принимая из соображений устойчивости Ω_УПТ/Ω'_{ср н} = 2, получим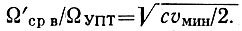

Подставляя этот результат в выражение для υ_мин, будем иметь

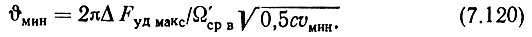
Теперь из (5.11) с учетом (5.87) определим максимальное расчетное значение полосы пропускания ЦФАПЧ

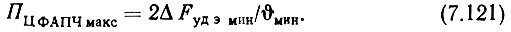
Сравним значения П_{ЦФАПЧ макс}, полученное из (7.121) и F'_М, полученное из построения на рис. 7.3. Если П_{ЦФАПЧ макс} < F'_M, то обеспечить заданные шумовые характеристики в рамках однокольцевого цифрового синтезатора невозможно и нужно применить двухкольцевой цифровой синтезатор по структурной схеме рис. 3.5. Если же П_{ЦФАПЧ макс} > F'_М, то система выполнима. Но

При B = 1 необходимо принять П_{ЦФАПЧ макс} = F'_М. Если же В > 1, то, как следует из (7.40), полосу пропускания кольца можно выбирать, выполняя двойное неравенство

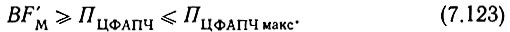
Кроме того, во всех случаях следует помнить, что полоса пропускания кольца ограничивается для случая идеального ФД выражением (3.29), а при реальном - условием П_{ЦФАПЧ макс} ≤ β₀/4 с.

ж. Определяем отношение постоянных времени пропорционально-интегрирующего ФНЧ, соответствующее выбранной полосе пропускания,

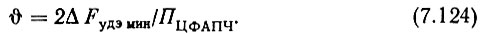
з. Из (5.29) определяем меньшую постоянную времени ФНЧ, задавшись коэффициентом затухания ξ = 1;

а по ней из (5.17) - круговую частоту Ω₂.

и. По (5.30) находим резонансную частоту кольца ω_р, а по (7.45) и рис. 5.3 - минимально возможное время установления синхронизма τ_уст.

к. Из (5.26) находим большую постоянную времени ФНЧ

а из (5.17) - соответствующую ей круговую частоту Ω₁.

л. Из (5.34) определяем полосу захвата ΔF_з.

м. Строим ЛАЧХ разомкнутого кольца (рис. 7.8), для чего:

- наносим на ось абсцисс с делениями в логарифмическом масштабе ω = Ω₁, ω = Ω₂ и ω = 1;

- из точки (1, 0) восстанавливаем перпендикуляр, равный 20 lg ΔΩ_{удэ мин} = 20 lg 2πΔF_{удэ мин} и через точку а на участке ω = 0÷ω = Ω₁ проводим прямую с наклоном -20 дБ/дек;

- на участке ω = Ω₁÷ω = Ω₂ из точки b проводим прямую bc с наклоном -40 дБ/дек;

- из точки с проводим прямую cd с наклоном -20 дБ/дек до пересечения с осью абсцисс; находим значение нижней частоты среза системы Ω_{ср н};

- проверяем, что

- из (7.119) определяем Ω_УПТ, а по (7.48) - Т_УПТ;

- продолжаем прямую cd до абсциссы Ω_УПТ (участок de);

- выбираем частоту Ω_ФД ≈ (50÷100) Ω_УПТ, наносим ее на график и проводим прямую eg с наклоном -40 дБ/дек; из (7.49) определяем постоянную времени нагрузки ФД Т_ФД;

- проводим из точки g в сторону увеличения частоты прямую с наклоном -60 дБ/дек.

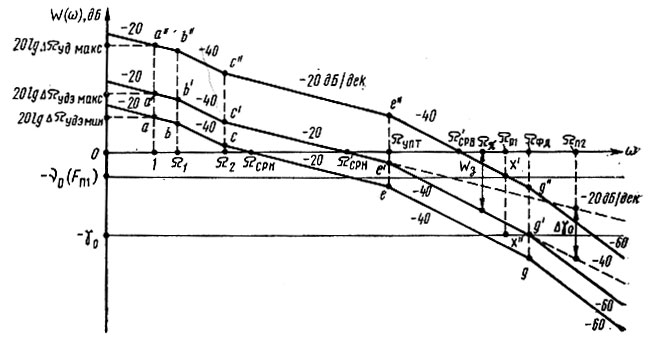
Рис. 7.8. Расчетные ЛАЧХ кольца ЦФАПЧ

н. Определяем

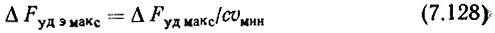
и по правилам, изложенным в предыдущем пункте, строим несмещенную ЛАЧХ системы при 20 lg ΔΩ_{удэ макс} = 20 lg 2πΔF_{удэ макс} - a'b'c'e'g' (рис. 7.8). Находим частоту среза Ω'_{ср н} и проверяем, что Ω'_{ср н} < Ω'_УПТ.

о. По правилам, изложенным в предыдущем пункте, строим смещенную ЛАЧХ системы при 20 lg ΔΩ_{уд макс} = 20 lg 2πΔF_{уд макс} - a"b"c"e"g" (рис. 7.8). При этом нестабильностями собственных частот звеньев пренебрегаем (они учитываются запасами по фазе и амплитуде).

п. Определяем степень подавления побочных составляющих кольцом ЦФАПЧ, для чего:

- проводим прямые [-ν₀(F_П1)_дБ] и (-γ_0[дБ]) до значения ω, соответствующего частоте Ω_п1 = 2πf_{q пр3};

- пренебрегая, как и ранее, влиянием на фильтрацию нагрузки ФД, по ординате точки х' определяем степень удовлетворения требованиям по подавлению помех с учетом фильтрующего действия фиксатора нулевого порядка; по ординате точки х проверяем тоже, но без учета действия фиксатора.

Подавление остальных помех, действующих в системе, смысла проверять нет, так как помеха с частотой f_{q пр3}, во-первых, является самой низкочастотной; во-вторых, должна быть подавлена кольцом полностью (вне кольца она ничем не подавляется, так как является полезным колебанием); в-третьих, частоты всех остальных возможных помех являются гармониками частоты f_{q пр3}, для которых фиксатор также является в определенной степени режекторным фильтром и, наконец, в-четвертых, кольцо ЦФАПЧ при Ω_п > Ω_УПТ подавляет каждую составляющую следующей гармоники частоты помехи на 12 дБ больше, чем предыдущей.

р. Определяем устойчивость системы по фазе по приближенным ф-лам (7.51) и (7.52), не прибегая к построению фазовой характеристики (см. § 7.2, п. 7и). При этом в (7.51) необходимо учесть запаздывание, вносимое фиксирующим устройством фазового дискриминатора в соответствии с (5.77):

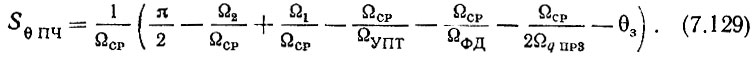
Расчет по (7.129) проводим для двух значений частоты среза Ω_{ср н} и Ω'_{ср н}, задавшись запасом по фазе θ₃ = 0,5÷0,8.

Полосу пропускания тракта промежуточных частот определяем по (7.52), подставив в это выражение минимальное из двух значений S_θПЧ, полученных из (7.129).

с. Запас по усилению W_з определяем так, как изложено в § 7.2, п. 7к, т. е., пользуясь выражениями (7.53)-(7.55), добавив в правые части первых двух, члены -Ω_УПТ/2Ω_{q пр3} и -Ω_ФД/2Ω_{q пр3} соответственно.

т. Пользуясь рис. 5.3 и выражением (7.57), находим максимальную скорость поиска L_{п макс}. Если система оказывается узкополосной и время установления синхронизма очень большим, то минимально возможное время перестройки (а отсюда, следовательно, и скорость перестройки) определяется

где П_п - полоса частот, в которой осуществляется перестройка. Реальное время τ_п следует считать примерно на порядок большим.

8. Расчет обеспечения коэффициентов гармоничности колебаний.

Для предотвращения "зеркальной настройки" на соседнюю опорную частоту ПФ должен иметь селективность, определяемую выражением (7.58).

Выше говорилось о том, что частоты любых помех в системе являются гармониками f_{q пр3} и режектируются фиксирующим устройством ФД. Однако из-за неидеальности ФД можно говорить, что коэффициент χ_ФД, определенный для f_{q пр3}, следует применять только к колебаниям первых двух-трех гармоник f_{q пр3}. Что же касается помех более высоких частот, то, в первую очередь, за счет паразитных проходных емкостей неидеальность ФД для них возрастает и, следовательно, коэффициент χ_ФД - также. Поэтому целесообразно в отношении этих помех принимать χ_ФД = 1 и для расчета использовать ф-лы (4.83) и (4.84).

Однако необходим, как и в случае применения активного многодекадного синтезатора учитывать фильтрующие свойства УПТ (влиянием нагрузки ФД, как и ранее, пренебрегаем). Методика этого учета изложена в предыдущем параграфе и иллюстрируется рис. 7.4 и рис. 7.8 для помехи Ω_п2. Таким образом, будем учитывать разности Δγ_0i(F_п) между ординатами реальной ЛАЧХ при ΔΩ_{удэ макс} и ЛАЧХ без учета действия УПТ (между участком ЛАЧХ с наклоном -40 дБ/дек и этим же участком с наклоном -20 дБ/дек). С учетом этих замечаний расчетные выражения для коэффициентов гармоничности колебаний опорных частот примут вид:

- для колебаний опорных частот f"_q

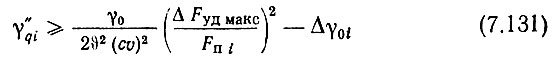
с проверкой по (4.72) и (4.63);

- для колебаний опорных частот f'_q в случае линейного безынерционного второго смесителя

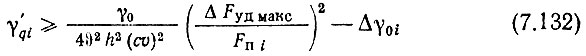
или по (7.131), если линейность и безынерционность смесителя нельзя получить или даже гарантировать.

Расчет коэффициентов гармоничности колебаний опорных частот по "полосным" помехам проводим по (4.73) и (4.75).

9. Расчет шумовых характеристик начинаем с приведения формы, в которой задана шумовая характеристика, по (7.64)-(7.66) к среднеквадратичному значению девиации частоты σ_0f.

Приравняв, в первом приближении, σ_{q пр f} = 0, из (4.132) получим (в секундах)

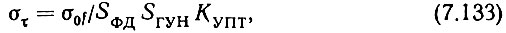
где

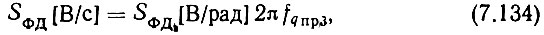
а в знаменатель (7.133) подставляются максимальные значения величин.

В соответствии с (4.137) находим коэффициент шума линейной части синтезатора

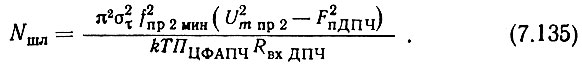
Из выражений (7.69), (7.70) и (4.116) находим шумовой параметр смесительного диода Ш_д, параметр отношения частот χ и, задавшись собственным коэффициентом шума первого смесителя N'_шСм1 ≈ 8÷10, - коэффициент Λ.

Из выражения (7.71) определяем коэффициент шума на выходе генератора гармоник старшего разряда N"_шq.

В соответствии с (4.140) найдем девиацию частотными шумами колебаний опорных частот σ"_qf. Найдем шумовую девиацию частоты колебаний ЭЧ

где m"n" - общий максимальный коэффициент умножения частоты в МОЧ.

Зная σ_q0f и коэффициент деления

находим шумовую девиацию частоты колебания, подаваемого на ФД,

Полученное значение σ_{q пр f} из (7.138) является вторым приближением. Подставив эту величину в (4.133), получим σ_τ во втором приближении

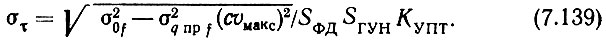
Далее производим расчет по приведенным выше формулам, начиная с (7.135). Обычно, однако, во втором приближении рассчитывать шумы не требуется.

10. Расчет системы генераторов гармоник производится в полном соответствии с материалами, изложенными в § 7.2, п. 10, т. е. входные параметры каждого генератора гармоник определяются: мощность - выражением (7.73), коэффициенты гармоничности колебаний - (7.74) и шумовая девиация частоты - (7.75).

Однако следует остановиться на одной особенности, специфичной для проектируемой системы. Генератор гармоник с выходными частотами f'_q генерирует колебания только двух гармоник частоты β₁, причем к коэффициентам гармоничности этих колебаний предъявляются достаточно жесткие требования (порядка 60 дБ и выше). Поэтому этот генератор гармоник целесообразнее заменить двумя ГОЧ с индивидуальными неперестраиваемыми фильтрами. Так как эти ГОЧ работают не одновременно, то они могут переключаться по выходам при помощи электронного переключателя или быть через общий выходной каскад подключены к смесителю, а переключаться по входам.

При таком решении задача проектирования МОЧ упрощается.

11. Расчет системы генераторов опорных частот производим по плану, изложенному в § 7.2, п. 11.

12. Расчет эталона частоты производится по тем же принципам и в том же порядке, что и для систем с многодекадными синтезаторами частот (см. § 7.2, п. 12).