3.2. Поверхностно-распределенные помехи

1. Помехи от морской поверхности. Отражения радиолокационного сигнала от морской поверхности определяются состоянием поверхности моря, зависящим от различных атмосферных факторов, наиболее важным из которых является ветер.

Общая взаимосвязь между скоростью ветра и состоянием поверхности моря оценивается, как правило, по шкале Бофорта [17], в которой в зависимости от скорости ветра представлены 13 состояний морской поверхности (от штиля до урагана). Для правильного выбора параметров РЛС в условиях воздействия отражений от морской поверхности необходимо знать плотность распределения вероятностей скорости ветра над поверхностью моря.

Морские волны характеризуются тремя факторами: длиной (L), высотой (H), периодом (T). Высота волны обычно оценивается вертикальным расстоянием от гребня до впадины, длина волны есть расстояние между двумя гребнями, скорость волны - это скорость приближения фронта волны. На внутренних морях даже в условиях шторма волны редко превышают 9 м по высоте, 150 м по длине и 10 с по периоду. Высота морских волн оценивается по-разному и обычно определяется действующей высотой, под которой понимается средняя высота одной трети измеренных волн, и обозначается H_1/3.

В [54] приводятся следующие соотношения для расчета параметра H_1/3: H_1/3 = 4,06 √σ²_h, где σ²_h - дисперсия высоты волны, и H_1/3 = 3,926 ⋅ 10^-4 υ³_в, где υ_в - скорость ветра, км/ч.

Помимо состояния моря важным фактором, влияющим на характеристику отраженного сигнала, является угол скольжения φ. На рис. 3.1 показана типичная зависимость S_S от угла φ, на которой можно выделить три характерные области. Зона между φ₂ и φ = 90° представляет собой область зеркального отражения, которое определяется элементами волн, размеры которых превышают длину волны РЛС. В области между φ₁ и φ₂ отражение главным образом происходит от капиллярных и гравитационных волн, длина которых соизмерима с длиной волны РЛС. Наконец, в третьей зоне (между нулем и φ₁) из-за интерференции между излучаемой и отраженной волнами наблюдается резкое уменьшение S_S при уменьшении угла падения φ.

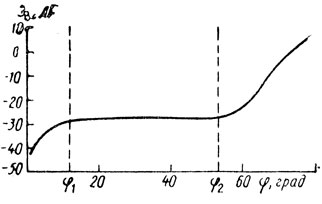
Рис. 3.1

В табл. 3.1 содержатся значения отражательной способности S_S в зависимости от угла скольжения, закона поляризации, состояния моря, несущей частоты [52], полученные экспериментально для зондирующих импульсов длительностью от 0,5 до 10 мкс.

Таблица 3.1

^* (Число в числителе характеризует S_S при вертикальной поляризации, а в знаменателе - при горизонтальной.)

Анализ экспериментальных данных, приведенных в таблице и в других источниках [54], позволяет установить характер влияния на отражательную способность несущей частоты, поляризации сигнала и состояния поверхности моря.

Связь между S_S и рабочей частотой РЛС f учитывается соотношением (по крайней мере для малых углов φ) вида S_S ∼ f^m, где m заключено в пределах от нуля до 4 [17].

Для углов (φ > 60° поляризация практически не оказывает влияния на отражательную способность. При малых углах φ горизонтальная поляризация дает заметно меньшие величины S_s, чем вертикальная поляризация. Эта разница уменьшается с ростом φ и К_В - показателя состояния моря по шкале Бофорта.

На основании экспериментальных данных установлена эмпирическая зависимость отражательной способности от φ, λ, К_В [17, 541:

где S_S, sin φ и λ выражены в децибелах. Эта зависимость справедлива в случае вертикальной поляризации для углов φ < 45°.

Экспериментально доказано также, что центр спектра помехи от морской поверхности сдвинут относительно несущей частоты за счет эффекта Доплера из-за движения волн. Центральную частоту спектра помехи f_оп можно определить из соотношения

где g - ускорение свободного падения; υ_в - скорость ветра, м/с; ε - угол между направлением ветра и лучом РЛС.

Энергетический спектр помехи с центром на f_оп является гаусссовским, а дисперсия зависит от высоты действующей волны:

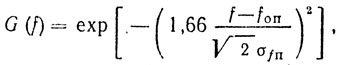(3.30)

где

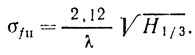(3.31)

Формула для σ_fп справедлива для РЛС с вертикальной поляризацией. При горизонтальной поляризации спектр более широкий, но по мере увеличения угла φ также определяется приведенной формулой.

При вращении антенны спектр принятого сигнала становится шире, причем его дисперсия увеличивается: σ²_Σ = σ²_fп + σ²_a, где σ²_fп определяется из (3.31), а σ²_a - дисперсия спектра помехи из-за вращения антенны определяется соотношениями (3.28) и (3.29).

2. Помехи от поверхности земли. Поверхность земли можно условно разделить на четыре типа:

А - гладкая (песчаная поверхность, озера, асфальтированная поверхность);

В - смешанная (холмистая местность с отдельными участками леса, с небольшим числом сооружений);

C - нерегулярная (гористая и лесистая местность);

D - городская местность.

Можно выделить три категории статистических данных, характеризующих, отражения от земли: временные, пространственные и спектральные.

Для конкретного типа РЛС временная статистика представляет собой распределения отражательной способности поверхности S_s в пределах одного элемента разрешения. Амплитудное распределение можно найти экспериментально при неподвижной антенне, определяя частоту появления различных значений S_s. Временные характеристики помех для различных элементов разрешения независимы друг от друга.

Плотность распределения вероятностей параметра S_s для каждого элемента разрешения в общем случае описывается законом Райса:

(3.32)

Предположение о гауссовской форме энергетического спектра отражений от земли подтверждено рядом экспериментов [17, 20, 54]:

σ_υ ∼ 0,0129 υ^1,3.

В приведенных формулах скорость ветра υ_в выражена в метрах в секунду.

Пространственное распределение, характеризующее зависимость параметров помех от дальности и азимута, можно определить, используя тот же метод, что и для определения временного распределения, т. е. необходимо измерить частоту появления заданного значения S_s, анализируя все элементы разрешения в пределах дальности действия РЛС. Таким образом можно получить функцию распределения параметра S_s для данной зоны.

На рис. 3.2 показана функция плотности распределения вероятностей р (S_s) для всех типов поверхности земли. Это распределение справедливо для малых углов скольжения φ < 1°. Видно, что все кривые имеют "хвост", лежащий значительно выше кривой рэлеевского распределения. Функция р (S_s) для поверхности типа А определялась для РЛС, работающей в 10-см диапазоне, типа С - в 5-см диапазоне, В и D - в 3-см диапазоне.

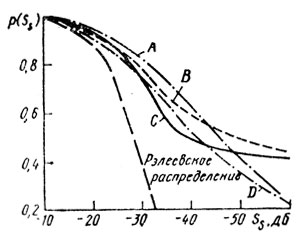
Рис. 3.2

Графики функции распределений F (S_s), представленные на рис. 3.3, близки к прямым линиям с одинаковыми наклонами. Это указывает на логнормальный тип распределения. Зависимости на рис. 3.3 получены для РЛС, работающей в 20-см диапазоне (1 - гористая местность с большим количеством растительности, 2 - холмистая местность с отдельными кустами, 3 - нерегулярная поверхность).

Рис. 3.3

Считается, что при малых углах скольжения вследствие маскирующего эффекта логнормальная зависимость наилучшим образом характеризует функцию распределения:

(3.34)

где S_SM - медианное значение S_s; ln S_SM - среднее значение от ln S_s; σ = [(ln S_s)¯² - (ln S_SM)²] - СКО величины ln S_s.

Логнормальная зависимость характеризуется двумя параметрами (медианой и математическим ожиданием) и позволяет учитывать значительные размеры "хвоста". Следовательно, основная задача состоит в оценке этих параметров, если известны характеристики РЛС и тип местности.

Как показано в § 3.1, при малых углах скольжения и высокой разрешающей способности плотность распределения p(S_s) может аппроксимироваться распределением Вейбулла. В табл. 3.2 приведены основные характеристики этого распределения в зависимости от угла скольжения параметров РЛС (диапазон 8-12,5 ГГц, длительность импульса 0,17 мкс) и вида поверхности земли.

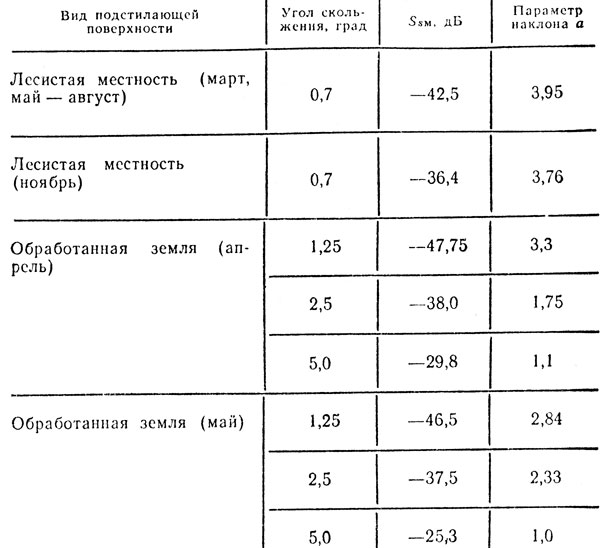
Таблица 3.2

На рис. 3.4 показана функция распределения вероятностей F(γ), где у определяется соотношением (3.9), для больших (> 5°) углов скольжения (1 - городская местность, 2 - местность, покрытая лесами, 3 - пустыня, 4 - распределение Рэлея). Очевидно, что рэлеевская аппроксимация является достаточно удовлетворительной.

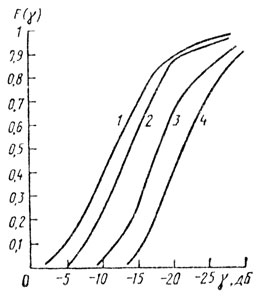
Рис. 3.4

Параметры, влияющие на отражение от земли. Помеховый сигнал зависит от рабочей частоты передатчика РЛС и поляризации, а его амплитуда - от электрических характеристик отражающей поверхности и объектов, имеющихся на этой поверхности. Помимо этого параметр S_s связан с дли тельностью зондирующего импульса, с высотой расположения антенны над землей, а также с изменением характеристик местности, вызываемых климатическими и метеорологическими условиями.

Для любой излученной волны λ местность может быть раз делена на гладкую и неровную. К гладкой относится местность, у которой среднее значение неровностей менее λ/(16 sin φ), в противном случае местность считается неровной. При всех характерных волнах радиолокационного диапазона (23, 10, 5 и 3 см) практически любая местность относится к категории неровных.

Для определения зависимости S_s от длины волны можно использовать следующую методику [54]. Из всех измеренных значений S_s выбираются только те, частота появления которых не превышает задан ной вероятности Р. Затем осуществляется группировка значений S_sP для радиолокационных диапазонов и четырех типов поверхности земли. После этого в пределах каждой группы экспериментальных данных находится средняя величина S¯_sP и строится зависимость S¯_sP от λ.

В табл. 3.3 приведены значения S¯_sP для Р = 0,84 и 0,5 для различных типов местности [54].

Таблица 3.3

Абсолютное значение S_s уменьшается с ростом f, но разность (S¯_{s 0,84} - S¯_{s 0,5}) остается практически постоянной при изменении и рабочей частоты, и типа местности. Значения S_sP, приведенные в таблице, были получены при углах скольжения от 5 до 10° при различных длительностях зондирующих импульсов (от 5 до 0,5 мкс), размерах азимутального луча (менее 0,8°) и поляризациях (вертикальной и горизонтальной). Величины, выбранные для заданных вероятностей, дают возможность определить параметры пространственно го распределения S_s. Если распределение предполагается логнормальным, то его параметры могут быть представлены медианным значением S_{s 0,5} и СКО σ_s = S_{s 0,84} - S_{s 0,5}.

Влияние на S_s угла скольжения φ. На рис. 3.5 приведены зависимости S_{s 0,5} от φ для различных типов местности для РЛС 3-см диапазона и τ_и = 1 мкс. Как показано в [54], для значений φ от 1 до 5° кривые можно аппроксимировать законом

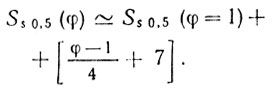(3.35)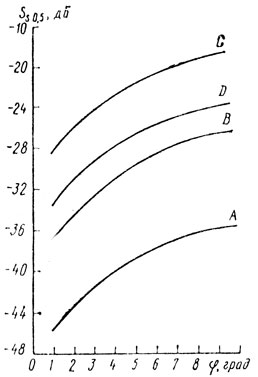

Рис. 3.5

Значение S_{s 0,5} (φ), определенное с помощью (3.35), измеряется в децибелах. Соотношение (3.35) справедливо и для S_{s 0,84}(φ). В случае когда φ изменяется от 10 до 60°, величина S_s практически не зависит от φ.

В последнее время на основании ряда экспериментальных данных были получены эмпирические уравнения для определения значений отражательной способности при малых углах скольжения [57].

Уравнение, справедливое для различных типов поверхности земли:

где С₁, С₂, С₃, φ₀, λ₀ - постоянные величины, значения которых для различных видов подстилающей поверхности даны в табл. 3.4.

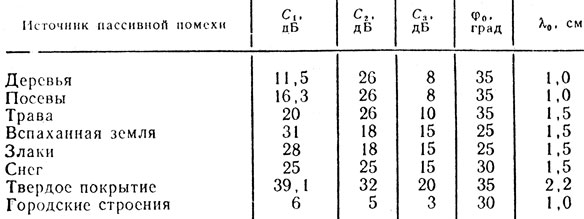
Таблица 3.4

Уравнение для поверхности земли, покрытой сухими деревьями, и поля, покрытого травой:

Влияние поляризации на S_s. Поляризация излучаемого сигнала не оказывает особого влияния на величину S_s для большинства типов местности. Но в целом при горизонтальной поляризации значения S_s оказываются меньшими, чем при вертикальной поляризации, разница может составлять 5 дБ для неровной поверхности.

Отражения, получающиеся при перекрестной поляризации, на 5-10 дБ меньше, чем при прямой. Это справедливо для всех типов поверхностей, за исключением городов и гор, выступы которых в заметной степени определяют зависимость интенсивности отражений от поляризации.

Влияние на S_s окружающих и климатических условий. Учет условий, в которых работает РЛС, сводится к оценке влияния метеорологических факторов (дождь, снег, ветер и т. д.) на рассчитываемые значения S_s. В качестве примера рассмотрим воздействие дождя на неровную поверхность. Этот пример интересен тем, что для плоской местности пленка воды, возникающая при дожде, увеличивает гладкость поверхности, что ведет к значительному росту вели чины S_s. Воздействие дождя на неровную поверхность за висит от количества растительности. В табл. 3.5 приведены значения S_s для холмистой местности, измеренные с помощью РЛС 3-см диапазона в разные месяцы [54] (длительность импульса 0,2 мкс, азимутальная ширина луча 1,4°).

Таблица 3.5

Полагая август самым сухим месяцем, можно прийти к выводу, что во время дождя S_s уменьшается в диапазоне 3 см примерно на 7 дБ. Можно предположить, что дождь оказывает такое же действие и в других радиолокационных диапазонах.

Что касается снега, то отраженный сигнал зависит от количества воды, содержащейся в снеге. В литературе имеется немного данных по этому вопросу (и все они относятся к 3-см диапазону) [54], из которых следует, что снег вызывает такое же уменьшение S_s, как и дождь (на 9-10 дБ).

Влияние на S_s длительности зондирующего импульса. Необходимо отметить следующее. Обычный метод, принятый для оценки S_s, состоит в измерении эквивалентного по перечного сечения элемента помехи S_п = S_sS с помощью РЛС и делении результата на S = (Rφ_α/L_дна) (τC/2) sec φ. На рис. 3.6 показано влияние длительности зондирующего импульса τ на плотность распределения вероятностей р(S_п) (РЛС 5-см диапазона) [52, 54]. Видно, что в зависимости от длительности импульса кривые имеют различные наклоны. Разницу в наклонах можно объяснить внутренней структурой помехи. Действительно, уменьшение длительности при водит к усилению влияния тех источников помехи, которые характеризуются зеркальным отражением, и тех, которые в любом случае преобладают. Иными словами, мощные точечные отражатели, действие которых маскируется в результате суммирования различных элементарных источников в пределах зоны S, где образуется сигнал помехи, оказываются изолированными, как и в случае затенения. Таким образом, при уменьшении τ и увеличении φ действие более мощных элементарных отражателей распределяется на меньшее число элементов в за данной исследуемой области.

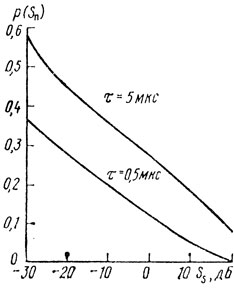
Рис. 3.6

При изменении τ значение S_{s 0,5} остается постоянным, в то время как значение S_{s 0,84} изменяется. Если распределение описывается логнормальным законом, то при уменьшении τ будет увеличиваться отношение между средним и медианным значениями.

Отражательная способность земной поверхности при облучении ее РЛС миллиметрового диапазона может характеризоваться следующим эмпирическим соотношением [58]:

где φ - угол падения, рад; σ_h - СКО неровности поверхности; C₁, С₂, С₃, С₄ - постоянные величины (определяются эмпирически).

Для очень неровных поверхностей выполняется не равенство σ_h/λ >> 1 и уравнение (3.36) принимает вид

Для очень гладких поверхностей (σ_h/λ << 1)

Таким образом, задав соответствующим образом постоянные коэффициенты C₁, С₂, С₃ и С₄, отражающая поверхность S_s может быть определена как функция угла скольжения φ.

Значения постоянных C₁, C₂, С₃ даны в табл. 3.6. Для выбранных источников пассивных помех С₄ = 0. На рис. 3.7 приведены зависимости S_s от угла скольжения φ при 10, 35 и 95 ГГц для различных источников пассивных помех (а - поверхность земли, покрытая сухим снегом, б - поверхность земли, покрытая мокрым снегом, в - лесистая поверхность).

Таблица 3.6

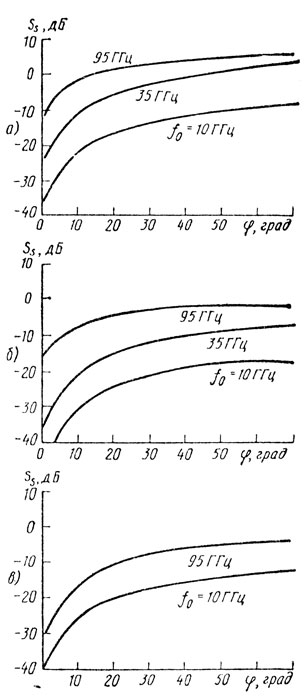
Рис. 3.7