Глава 3. Характеристики пассивных помех

3.1. Основные характеристики пассивных помех

Сигналы, отраженные от источников пассивных помех, характеризуются: плотностью распределения вероятностей амплитуды и мощности флуктуации отраженного сигнала или эффективной площади рассеяния пассивной помехи, а также спектрально-корреляционными характеристиками. При рассмотрении плотности распределения вероятностей амплитуды флуктуации обычно берут модель помехи в виде множества независимых отражающих элементов, хаотично распределенных в элементе разрешения. В этом случае плотность распределения вероятностей амплитуды отраженного сигнала подчиняется закону Рэлея:

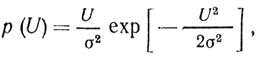(3.1)

где U - амплитуда отраженного сигнала; σ² - дисперсия амплитуды.

Рэлеевское распределение характерно для местностей, покрытых густой растительностью. Флуктуирующая составляющая при этом связана с перемещением отражателей под действием ветра, а стационарная составляющая практически отсутствует. В том случае когда существует один отражатель, который формирует мощный сигнал помехи, окруженный рядом менее интенсивных отражателей, необходимо использовать распределение Райса:

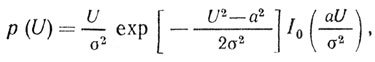
где а - стационарная составляющая помехового сигнала; I₀( ) - функция Бесселя нулевого порядка от мнимого аргумента.

Мощность результирующего помехового сигнала распределяется по экспоненциальному закону:

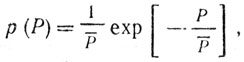(3.2)

где Р - мощность помехового сигнала; Р‾ - средняя мощность помехового сигнала.

Учитывая, что эффективная поверхность рассеяния пропорциональна мощности отраженного сигнала, то в соответствии с формулой (3.2) закон распределения эффективной площади рассеяния представим в виде

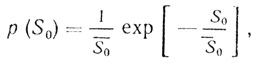(3.3)

где S‾₀ - среднее значение ЭПР.

И, наконец, для относительной ЭПР S₀/S‾₀ распределения (3.3) можно записать в виде

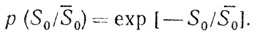(3.4)

Параметры всех приведенных распределений зависят как от параметров источника пассивных помех, так и от характеристик самой РЛС. И хотя для проведения сравнительных оценок рэлеевское распределение амплитуд (экспоненциальное распределение мощности) можно считать приемлемым, в некоторых практически важных ситуациях статистика помехи отличается от рэлеевской.

Нерэлеевская статистика пассивной помехи возникает тогда, когда подстилающая поверхность облучается РЛС с высокой разрешающей способностью (τ < 0,5 мкс) под малыми углами скольжения (φ ≤ 5°).

Для описания пассивных помех при указанных условиях было предложено использовать логарифмически-нормальное распределение вероятности амплитуд:

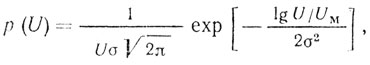(3.5)

где U_M - медиана распределения; σ² - дисперсия lgU² и распределение Вейбулла

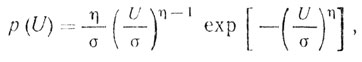(3.6)

где η - параметр формы; α = σ^η - параметр масштаба; η > 0; α > 0.

При η = 1 распределение Вейбулла становится экспоненциальной функцией плотности распределения амплитуды отраженного сигнала, а при η = 2 - рэлеевской.

Помимо указанных распределений для описания огибаю щей пассивных помех можно использовать составное или полигауссовское распределение, которое представляет собой сумму нескольких, например двух, гауссовских распределений с различными дисперсиями [15, 16]:

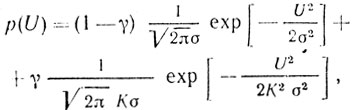(3.7)

где γ - весовой коэффициент; К² - отношение дисперсий двух Гауссовских плотностей распределения.

Для мешающих отражений в качестве меры их интенсивности широко применяется такая характеристика, как отражательная способность пассивной помехи (или коэффициент обратного рассеяния единичного объема или единичной площади поверхности, содержащих источник пассивной помехи, или удельная ЭПР), которую будем обозначать через S_s для поверхностно-распределенных и S_υ для пространственно (объемно)-распределенных источников пассивных помех.

Поверхностно-распределенные цели с помощью параметра S_s могут характеризоваться средней ЭПР единицы площади поверхности:

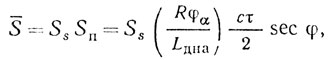(3.8)

где S_п - площадь элемента разрешения; τ - длительность импульса; φ - угол скольжения (под которым понимается угол между направлением распространения падающей радиоволны и касательной к поверхности раздела двух сред в точке падения радиоволны); R - наклонная дальность от РЛС до элемента подстилающей поверхности; φ_α - ширина луча ДНА на уровне 0,5 в азимутальной плоскости; L_дна - потери из-за аппроксимации ДНА.

Поверхности, для которых S_S = 0,1, будут обладать ЭПР, равной 0,1 м² на каждый квадратный метр площади облучаемой РЛС.

Иногда отражательная способность определяется параметром

Если S_S задается в децибелах, например S_S = -30 дБ, то это означает, что ЭПР пассивной помехи на 30 дБ меньше, чем у цели с ЭПР, равной 1 м².

Для объемно-распределенных источников пассивных помех соответствующим параметром является отражательная способность S_υ, характеризующая ЭПР единицы объема и имеющая размерность м²/м³ или (единица длины)^-1. Средняя ЭПР в пределах каждого элемента разрешения будет

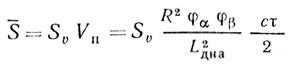(3.10)

где φ_β - ширина луча ДНА на уровне 0,5 в вертикальной плоскости.

Потери из-за аппроксимации диаграммы направленности антенны L_дна определяются экспериментально. При работе ДНА на прием и передачу L_дна = √2. Для гауссовской аппроксимации ДНА, а также для аппроксимации за коном sin x/x значение L_дна = √(8 ln 2/π) = 1,33.

В общем случае формула для расчета коэффициента S_υ для оценки отражательной способности метеообразований в сантиметровом диапазоне волн имеет вид

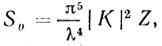(3.11)

где

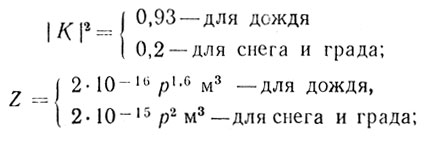
р - интенсивность выпадения осадков, мм/ч.

Соотношение (3.11) справедливо для случая согласования поляризации отраженного сигнала с приемной антенной. Если же закон поляризации отраженного сигнала не соответствует приемной антенне, то отражательная способность объемно-распределенного источника пассивных помех

За последнее время появилось большое число работ, посвященных анализу эффективности РЛС в случае, когда отражательная способность описывается с помощью распределения Вейбулла [56]. Рассмотрим методику анализа экспериментальных данных, позволяющих определить, подчиняются ли они распределению Вейбулла. Пусть

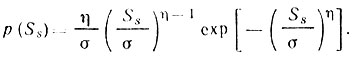(3.13)

Полагая η = 1 и α = σ^η = S‾_s, получаем экспоненциальное распределение

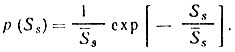(3.14)

Функция распределения определяется соотношением

Математическое ожидание при замене переменной x = S^η_S/α

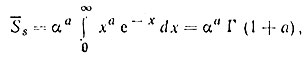(3.16)

где а = η^-1.

Уравнение (3.15) может быть записано в следующем виде:

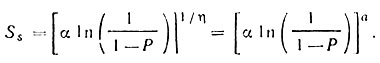(3.17)

Тогда медиана распределения определяется из (3.17) при Р = 0,5:

откуда

С учетом этого соотношения

Существуют аналитические методы определения функции распределения S_S, а также оценки параметров η и S_SM, однако графоаналитический метод является наиболее удобным при анализе экспериментальных данных.

Подставив (3.19) в (3.18), получим

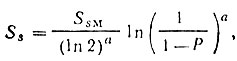
которое можно представить в виде

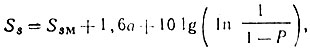(3.21)

где S_S выражается в децибелах.

Из этого соотношения видно, что если экспериментальные данные нанести на график с координатами lg [ln ¹/_1-P] по оси ординат и S_S в децибелах по оси абсцисс, то зависимость, соответствующая закону Вейбулла, будет представлять собой прямую линию, наклон которой определяется параметром а. Значение S_SM фиксирует лишь относительное положение линии распределения.

Заметим, что (3.21) может быть использовано при формировании распределения Вейбулла на ЦЭВМ, если

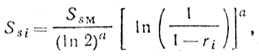(3.22)

где r_i - случайное число, равномерно распределенное от 0 до 1. Параметры а и S_SM предварительно задаются для конкретного вида помех. Параметр наклона а распределения Вейбулла может быть определен непосредственно из графика распределения Вейбулла. Еще раз напомнив, что шкала вероятности пропорциональна величине lg [ln ¹/_1-P], введем переменную х = lg [ln ¹/_1-P], такую, чтобы шкала вероятности преобразовалась в линейные единицы величины х. Подставляя х в уравнение (3.21), получаем S_S = S_SM + 1,6а + 10 ах.

Искомый наклон равен производной

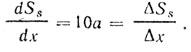
Отсюда получим

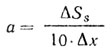(3.23)

Удобно определять параметр наклона а, когда Δх = 1. Пусть наименьшая вероятность Р = 0,1. Тогда:

Решив относительно Р' уравнение

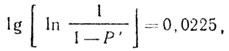
получим, что Р' = 0,651. И окончательно

a = (S_sP=0,651 - S_sP=0.1)/10.

Кроме амплитудного распределения сигнала помехи, а также отражательной способности источника пассивной помехи большую роль при разработке и анализе эффективности РЛС СДЦ играет энергетический спектр отражений. В многочисленных работах было показано, что энергетический спектр сигналов, отраженных от источников пассивных помех почти всех типов, можно представить гауссовским законом:

где G₀ - плотность мощности сигнала от источника помехи на нулевой частоте флуктуации; f₀ - рабочая несущая частота РЛС; а - безразмерная величина, характеризующая относительную стабильность отраженного сигнала. Значения а изменяются от 3,9⋅10⁹ для редкого леса в безветренный день и до 2,8⋅10⁵ для дождевых облаков.

Энергетический спектр может быть выражен через среднеквадратическое отклонение частоты сигнала помехи σ_fП:

где σ_υ - среднеквадратическое отклонение скоростей рассеивающих элементов. Очевидно, что

Одним из основных факторов, определяющих ширину спектра пассивной помехи, является движение антенны при сканировании [63]. Предположим, что диаграмму направленности антенны можно аппроксимировать нормальным законом:

где K = (1,66/φ_α)². Учитывая соотношение α/φ_α = t/T_обл, где Т_обл - время облучения цели, можно показать, что соответствующая этому закону корреляционная функция имеет вид

где Ω = 1,66/T_обл.

Вычислив Фурье-преобразование, получим

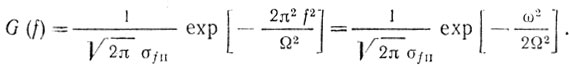
Из последнего соотношения видно, что Ω - есть среднеквадратическое отклонение (СКО) угловой частоты помехи, т. е. Ω = 2πσ_fП.

Учитывая, что n = F_ПТ_обл, окончательно имеем

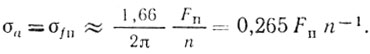(3.28)

Для случая аппроксимации ДНА законом sin x/x

В случае РЛС с фазированной антенной решеткой σ²_а = 0.

Помимо гауссовского распределение спектра сигналов, отраженных от поверхности земли, может подчиняться другим законам. Особенно это проявляется при ветреной погоде.

Так, в [54] указывается, что для РЛС, работающих в диапазонах 10 и 35 ГГц, энергетический спектр отражений от лесистой поверхности подчиняется экспоненциальному закону

где b - коэффициент, обратно пропорциональный логарифму скорости ветра.

Там же указывается, что при определенных условиях для РЛС, работавшей в диапазоне 10 ГГц, энергетический спектр сигнала, отраженного от лесистой поверхности, может быть аппроксимирован законом

где С - параметр, зависящий от частоты излучаемого сигнала и скорости ветра. Очевидно, что в этом случае при энергетическом спектре [1 + х³]^-1 в полосу режекции могут попасть сигналы целей, скорость которых мала. Это может привести к пропуску сигналов от них и соответственно к снижению эффективности РЛС.