
4.2. Характеристики, определяющие эффективность режекторного фильтра
1. Коэффициент подавления пассивной помехи. Для характеристики эффективности фильтра СДЦ можно использовать коэффициент подавления помехи (Кп), который определяется как отношение мощности помехи на входе устройства режекции к мощности пассивных помех на его выходе:
Кп = Рп вх/Рп вых. (4.1)
Этот коэффициент легко измерить. Однако он недостаточно полно описывает устройство режекции пассивной помехи, так как не учитывает прохождение полезного сигнала и влияние собственных шумов приемника.
В качестве примера использования Кп для оценки эффективности режекторного фильтра определим его значение для одно- и двухкратной схемы ЧПК. Полагая, что:
Gп(f) = G0 exp (-f2/2σ2fп); K1(f) = 4 sin2 (πf/Fп); (4.2)
К2(f) = 16 sin4 (πf/Fп), (4.3)
получаем следующие соотношения для расчета Рп вх и Рп вых:
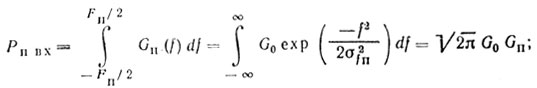 (4.4)
(4.4)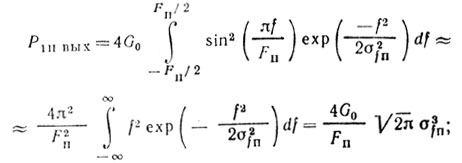 (4.5)
(4.5) (4.6)
(4.6)Замена пределов интегрирования в уравнениях (4.5) и (4.6), равных бесконечности, справедлива при σfп << Fп. Подставляя (4.4), (4.5) и (4.6) в (4.1), получаем:
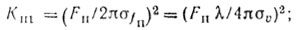 (4.7)
(4.7)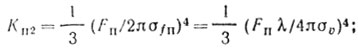 (4.8)
(4.8)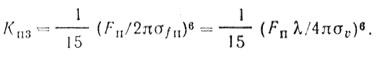 (4.9)
(4.9)Коэффициент подавления можно выразить через межпериодный коэффициент корреляции пассивной помехи ρ (Тп). Запишем выражение для сигнала на выходе схемы однократной ЧПК:
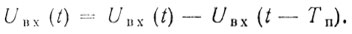
Так как предсказать значение остатка компенсации в любой момент времени невозможно, то следует его усреднить по всему ансамблю выходных сигналов:
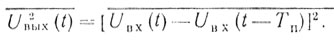
Для стационарных случайных процессов
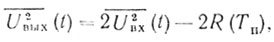
где R(Tп) - корреляционная функция помехи, определенная в момент τ = Тп.
Учитывая, что )U2вых(t)) = Рп вых; U2вx(t) = Рп вх; R(0) = Рп вх и ρ(Тп) = R(Тп)/R(0), получаем
Кп1 = 0,5 [1 - ρ(Тп)]-1. (4.10)
Проводя аналогичные рассуждения, можно показать, что для схем двухкратной и трехкратной ЧПК:
Кп2 = 0,5 [3 - 4ρ (Тп) + ρ (2Тп)]-1; (4.11)
Кп2 = 0,5 [10 - 15ρ (Тп) + 6ρ (2Тп) - ρ (3Тп)]-1, (4.12)
где ρ (2Тп) = R(2Тп)/R(0); ρ (3Тп) = R(3Тп)/R(0).
2. Коэффициент улучшения. Показателем качества функционирования фильтра СДЦ с амплитудно-частотной характеристикой |К(f)| для сигнала с энергетическим спектром Gc(f) и помехи с энергетическим спектром Gп(f) является коэффициент улучшения Ку, определяемый следующим образом [21]:
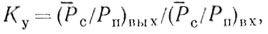 (4.13)
(4.13)где (Р¯с/Рп)вых и (Р¯с/Рп)вх - выходное и входное отношения мощности сигнала к мощности пассивных помех соответственно, усредненные по всем скоростям целей.
Этот параметр учитывает и ослабление пассивных помех в фильтре СДЦ и средний выигрыш фильтра СДЦ. Коэффициент улучшения является, таким образом, показателем отклика фильтра СДЦ на сигналы пассивных помех по отношению к усредненному отклику на сигналы от целей.
Соотношение (4.13) можно записать следующим образом:
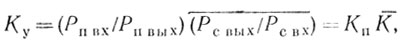 (4.14)
(4.14)где К¯ - средний коэффициент усиления мощности сигнала. При этом предполагается, что сигнал от цели имеет постоянную амплитуду, радиальная скорость цели равновероятна для всего диапазона значений. Предполагается также, что помеха является узкополосной с центральной частотой, которая совпадает с центром полосы режекции фильтра СДЦ, и приемник обладает сколь угодно большим динамическим диапазоном.
Соотношение (4.14) может быть представлено иначе, если учесть, что для собственных шумов приемника также сохраняется свойство равновероятности распределения по частотному диапазону, и, следовательно, справедливо соотношение
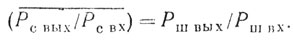 (4.15)
(4.15)Отношение Рш вых/Рш вх есть коэффициент усиления собственных шумов приемника режекторным фильтром Кш, и тогда
Ку = КпКш. (4.16)
Как следует из определения коэффициента улучшения, для его вычисления необходимо знать мощность остатков пассивных помех Рп вых. На эту величину оказывают влияние нестабильность элементов системы СДЦ (фазовые и амплитудные нестабильности, дрожание импульсов), движение антенны, вобуляция периода повторения и т. д. [8, 21, 52]. Влияние каждого отдельного фактора можно учесть и оценить через результирующий коэффициент улучшения. Если перечисленные факторы, влияющие на уровень остатков пассивной помехи, статистически независимы, то суммарная мощность остатков помехи Рп вых равна сумме мощностей остатков отдельных факторов:
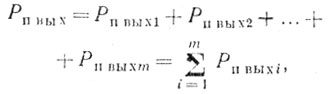
где m - число факторов, формирующих остатки компенсации пассивных помех.
Тогда коэффициент улучшения всей системы оценивается через коэффициенты улучшения каждой подсистемы с помощью соотношения
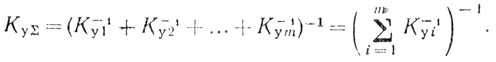 (4.17)
(4.17)Коэффициент улучшения, определяемый соотношением (4.17), учитывает как внешние, так и внутренние источники, способствующие формированию остатков пассивных помех.
Выше отмечалось, что данные определения предполагают, что режекторный фильтр работает с неограниченным динамическим диапазоном. Поясним важность этого условия.
Запишем выражение для коэффициента улучшения следующим образом:
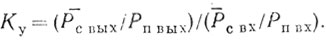 (4.18)
(4.18)Учитывая, что собственные шумы приемника также снижают эффективность СДЦ, приведем выражение (4.18) к виду
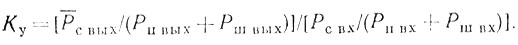 (4.19)
(4.19)Так как обычно выполняется условие Рп вх >> Рш вх и для высокоэффективных систем СДЦ остатки компенсации пассивных помех должны быть меньше, чем уровень собственных шумов приемника, т. е. Рп вых < Рш вых, то
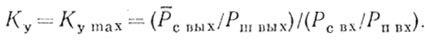 (4.20)
(4.20)Таким образом, качество работы высокоэффективных систем СДЦ определяется отношением сигнала к собственным шумам приемника. В этом случае имеется возможность связать отношение сигнал-шум с вероятностями правильного обнаружения и ложной тревоги. Очевидно, что соотношение (4.20) определяет максимально достижимое значение коэффициента улучшения.
Обзорные РЛС СДЦ работают в различной помеховой обстановке, поэтому не всегда может быть справедливо предположение о том, что остатки пассивных помех ниже уровня собственных шумов приемника.
Тогда коэффициент улучшения может быть определен следующим образом:
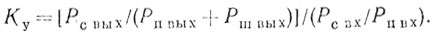 (4.21)
(4.21)Очевидно, что величина Ку, соответствующая (4.21), меньше Ку max.
В том случае когда Рп вх >> Рш вых, необходимо использовать соотношение (4.18), которое полностью совпадает с (4.13) и является стандартным выражением коэффициента улучшения, получившего наибольшее распространение. При этом для определения характеристик обнаружения РЛС СДЦ необходимо знать статистику остатков помех.
Следовательно, коэффициент улучшения не является фиксированной количественной величиной для фильтра СДЦ, а существенно зависит от помеховой обстановки, в которой работает РЛС СДЦ, и от режима работы трактов СВЧ и промежуточной частоты. Количественные значения Ку корректны только в том случае, когда заданы конкретная помеховая обстановка и характеристики предыдущих трактов обработки радиолокационной информации, для которых они получены.
В связи с этим необходимо ввести понятие линейного динамического диапазона РЛС. Будем считать, что линейный динамический диапазон определяется соотношением
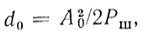 (4.22)
(4.22)где А0 - уровень сигнала на входе УПЧ, при котором выходной сигнал снижается до уровня, который позволяет считать обработку линейной (обычно этот уровень не превышает 1 дБ).
Одновременно, учитывая, что одним из основных требований, предъявляемых к РЛС СДЦ, является обеспечение ПУЛТ, целесообразно ввести параметр - динамический диапазон схемы, обеспечивающий ПУЛТ и определяемый как максимальный динамический диапазон, при котором выполняется условие Рш > Рп вых:
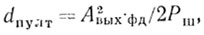 (4.23)
(4.23)где Авых фд - максимальная амплитуда сигнала на выходе фазового детектора. Очевидно, что Ку ≥ dпулт, а dпулт > d0.
Здесь же необходимо отметить, что если только две РЛС СДЦ работают в различных помеховых обстановках, то даже при одинаковых значениях Ку они имеют разные значения вероятностей правильного обнаружения и ложной тревоги.
В заключение этого параграфа приведем формулы для расчета Ку для систем ЧПК различной кратности. В [52] показано, что для n-кратной схемы ЧПК
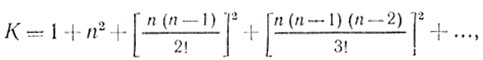 (4.24)
(4.24)т. е. для однократной ЧПК К = 2 (3 дБ); для двухкратной ЧПК К = 6 (7 дБ); для трехкратной ЧПК К = 20 (13 дБ) и т. д.
Тогда для расчета Ку получим следующие соотношения:
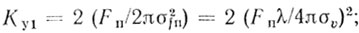 (4.25)
(4.25)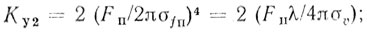 (4.26)
(4.26)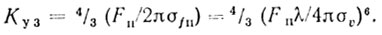 (4.27)
(4.27)Используя соотношения (4.10)-(4.12) и (4.24), находим:
КУ1 = [1 - ρ(TП)]-1; (4.28)
КУ2 = 3 [3 - 4ρ(TП) + ρ(2TП)]-1; (4.29)
КУ3 = 10 [10 - 15ρ(TП) + 6ρ(TП) - ρ(3TП)]-1. (4.30)
Соотношения (4.25)-(4.27) не учитывают влияния средней скорости помехи υп, которая может существенно повлиять на эффективность системы СДЦ. Полагая, что спектр помехи описывается нормальным законом, можно получить следующие формулы для расчета при однократной и двухкратной ЧПК [52]:
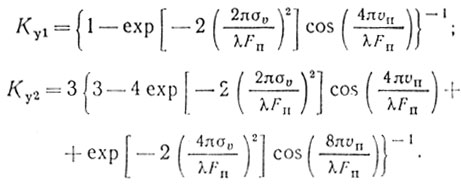 (4.31)-(4.32)
(4.31)-(4.32)Аргументы экспоненциальной и косинусоидальной функций в выражениях (4.31) и (4.32) намного меньше единицы, и поэтому можно получить их хорошую аппроксимацию, ограничиваясь двумя первыми членами рядов Тейлора для е-x и cosx в (4.31) и тремя первыми членами в (4.32). Тогда:
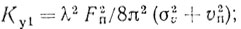 (4.33)
(4.33)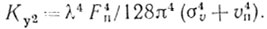 (4.34)
(4.34)Очевидно, что при υп = 0 соотношения (4.33) и (4.34) полностью совпадают с (4.25) и (4.26). Как следует из (4.33) и (4.34), наличие υп может существенно снизить эффективность устройств СДЦ. Особенно это важно, когда источником пассивных помех являются метеообразования, стаи птиц, облака диполей.
Рассмотрим теперь влияние на Ку сканирования антенны, которое вызывает расширение спектра пассивных помех вследствие амплитудной модуляции отраженных сигналов ДНА.
В гл. 3 показано, что для гауссовской аппроксимации ДНА
σfп = 0,265Fпn-1, (4.35)
а для аппроксимации законом sin х/х
σfп = 0,274Fпn-1. (4.36)
Подставляя (4.35) и (4.36) в (4.25)-(4.27), получаем для гауссовской ДНА:
КУ1 = 0,72 n2; КУ2 = 0,26 n4; КУ3 = 0,0625 n6; (4.37)
для ДНА типа sin х/х:
КУ1 = 0,675 n2; КУ2 = 0,228 n4; КУ3 = 0,0514 n6. (4.38)
Для гауссовской ДНА в [62] приведены следующие соотношения для расчета Kу некогерентной РЛС СДЦ:
КУ1 = 0,36 n2; КУ2 = 0,13 n4. (4.39)

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
