4.4. Влияние ограничения сигналов в тракте промежуточной частоты на эффективность СДЦ

В большинстве случаев при разработке РЛС включение перед схемами компенсации пассивной помехи линейного усилителя с ограничением обосновывалось необходимостью иметь такой уровень остатков пассивных помех, чтобы при отображении на экране индикатора они были похожи на собственные шумы приемника как по уровню, так и по тон кой структуре. Это необходимо прежде всего для обеспечения заданного уровня ложных тревог. Другой причиной включения ограничителя является то, что динамический диапазон устройств режекции пассивных помех не превышает 40-50 дБ, в то время как на входе РЛС он может превышать 100 дБ.

В предыдущих разделах было показано, что первоочередной задачей при разработке РЛС СДЦ является обеспечение линейности приемного тракта перед устройством режекции пассивных помех. Прежде чем перейти к анализу методов, обеспечивающих выполнение этого условия, рассмотрим вопрос, связанный с оценкой влияния ограничителя, включенного в тракте промежуточной частоты, на эффективность СДЦ.

Так как зондирующий сигнал представляет собой последовательность импульсов, то спектр помехи на входе ограничителя имеет дискретный характер. Гауссовская форма этого спектра является хорошей аппроксимацией в большинстве практически важных случаях и описывает ситуацию, когда большое число независимых факторов определяет расширение спектра. Так как выполняется условие σ_fп << F_п, анализ проводится в окрестности значений частоты f = f_0п. Тогда нормированный энергетический спектр помехи на входе

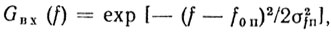(4.43)

где σ²_fп является единственным параметром, который характеризует спектр помех.

Влияние ограничителя в тракте промежуточной частоты на сигналы помехи может быть легко оценено с помощью функций корреляции. Корреляционная функция на входе ограничителя имеет вид

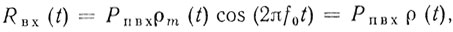(4.44)

где ρ_m(t) - огибающая корреляционной функции, равная

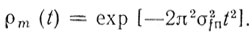(4.45)

Будем рассматривать ограничитель с характеристикой [62, 63]:

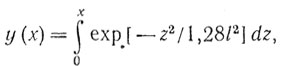(4.46)

где l - уровень ограничения сигнала.

Выходная корреляционная функция связана с входной соотношением [63]

где

Уравнение (4.47) при α = 0 дает хорошо известный результат, справедливый для жесткого ограничителя [63]:

Разлагая arcsin x в уравнении (4.47) в ряд, получаем

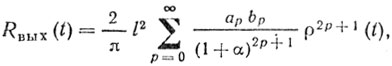(4.50)

где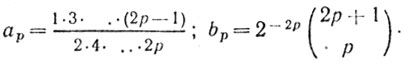

Фурье-преобразование уравнения (4.50) позволяет найти энергетический спектр G_{п вых}(f).

Полагая, что

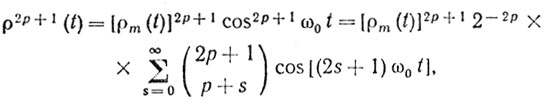(4.51)

и учитывая фильтрацию по несущей на промежуточной частоте (т. е. S = 0), получаем выходной спектр помехи:

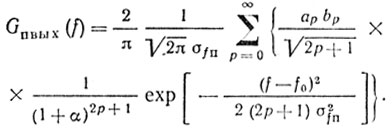(4.52)

Следовательно, прохождение сигналов через нелинейный элемент (ограничитель), включенный в тракте про межуточной частоты, является причиной расширения спектра помехи на выходе. В случае гауссовского входного спектра уравнение (4.52) показывает, что выходной спектр представляется бесконечным числом гауссовских слагаемых, дисперсии которых возрастают с ростом их нечетных номеров. Очевидно, что для получения хорошего приближения к G_{п вых}(f) необходимо учитывать как можно больше членов ряда.

Подставив соотношение (4.50) в (4.28) и (4.29), получим следующие формулы для расчета К_у с учетом включения ограничителя в тракте промежуточной частоты:

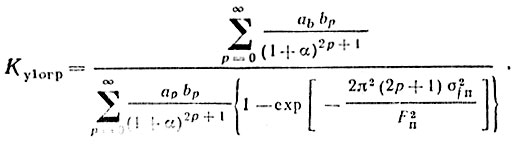(4.53)

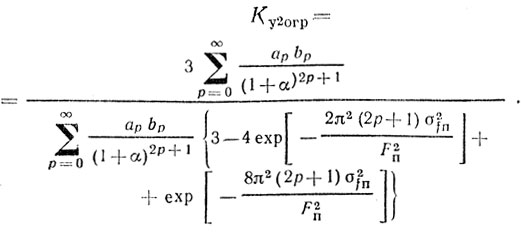(4.54)

Формулы (4.53) и (4.54) просто представить как функции числа импульсов в пачке, воспользовавшись соотношением (4.35).

На рис. 4.2 представлены изменения К_у в зависимости от интенсивности помех, относительно уровня ограничения для нескольких значений n для однократной ЧПК (штриховые линии) и двухкратной схемы ЧПК (непрерывные линии), а на рис. 4.3 - зависимости асимптотических значений К_у от n [63].

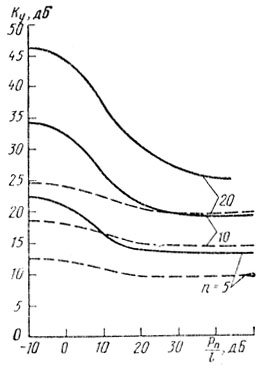
Рис. 4.2

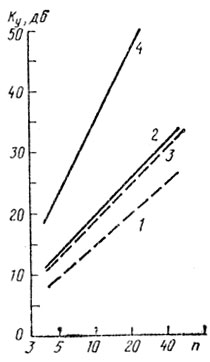
Рис. 4.3

Как следует из анализа приведенных зависимостей, К_у изменяется по закону, близкому к линейному, что позволило получить достаточно простые приближенные формулы для расчета К_у при наличии ограничителя в тракте промежуточной частоты [62, 63]:

Для некогерентной РЛС СДЦ:

На рис. 4.4 показаны кривые, характеризующие зависимость потерь L, возникающих из-за включения ограничителя в тракте промежуточной частоты, от n для однократной (штриховые линии) и двухкратной (непрерывные линии) ЧПК.

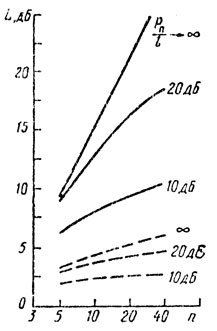
Рис. 4.4