6.2. Оптимизация весовых функций линейного режекторного фильтра

Обозначим сигнал, поступающий на вход линейного фильтра в дискретные моменты времени, как

где n(t) - стационарный случайный гауссовский процесс; φ - случайный параметр сигнала. Предположим также, что принимается ограниченная последовательность импульсов (пачка из n импульсов). Сигнал на выходе фильтра определяется соотношением

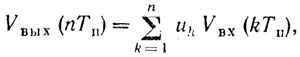(6.2)

где

u_n = {u₁, u₂, ..., u_n} = {x₁, x₂, ..., x_n) + i {y₁, y₂, ..., y_n}

комплексная весовая функция или вектор; u_n - комплексные числа; x и y - действительные числа.

Очевидно, что действительные и мнимые части весовой функции должны быть объединены с тем, чтобы сформировать физически реализуемую величину.

Средняя мощность на выходе фильтра

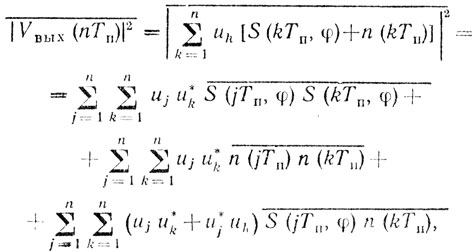(6.3)

где "*" означает комплексно-сопряженную величину; (¯) - операцию статистического усреднения по φ или по {n(t)}. Как отмечалось выше, предполагается, что n(t) - стационарный случайный процесс в широком смысле, с нулевым средним значением и корреляционной функцией вида

где ρ(τ) - нормированная корреляционная функция.

С учетом сделанных замечаний соотношение (6.3) может быть записано следующим образом:

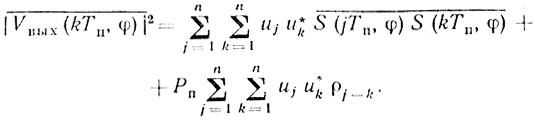(6.5)

Очевидно, что отношение сигнал-помеха на выходе фильтра на определенной доплеровской частоте равно отношению первого слагаемого в (6.5) ко второму:

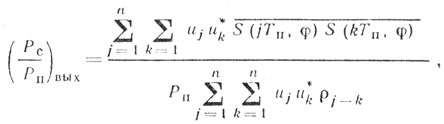(6.6)

где

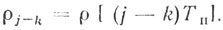(6.7)

Отношение сигнал-помеха на входе линейного фильтра

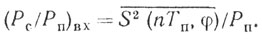(6.8)

Таким образом, эффективность линейного режекторного фильтра можно определить через коэффициент улучшения для заданной доплеровской частоты:

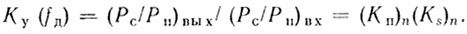(6.9)

Здесь

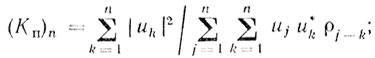(6.10)

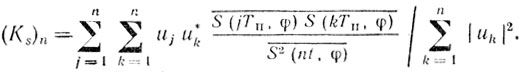(6.11)

Величина (К_п)_n не зависит от характеристик сигнала, а для фиксированного значения n зависит только от ρ(τ) и {U_n}. Коэффициент (K_s)_n для фиксированного n зависит только от характеристик сигнала и от {U_n}. Желательно, чтобы критерий оптимальности не зависел от характеристик сигнала. Тогда оптимальной весовой функцией, которая определяется вектором {U_n}, будет функция, максимизирующая величину (К_п)_n.

Основной недостаток приведенного определения заключается в том, что оптимальная весовая функция может сформировать небольшое значение коэффициента (K_s)_n, что, в свою очередь, несколько снизит К_у(f_д). Однако это неизбежно и является ценой за введение такого критерия оптимальности, который не зависит от характеристик сигнала.

Из (6.10) следует, что (К_п)_n - обратная нормированная квадратичная форма. Ее максимальное значение равно обратному наименьшему собственному значению корреляционной матрицы

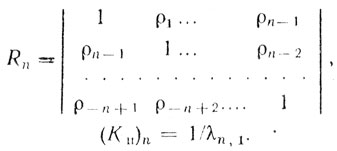(6.12)

Это справедливо в том случае, когда {U_n} является собственным вектором, соответствующим данному собственному значению [70]. Так как R_n - неотрицательно определенная матрица, то ее собственные значения являются действительными и неотрицательными числами. Определим оптимальные весовые функции для корреляционных матриц при n = 2 и 3 [70].

При n = 2 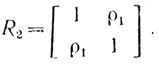(6.13)

Собственные значения удовлетворяют уравнению

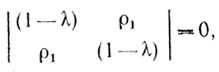(6.14)

так что:

Элементы собственного вектора U₂ должны удовлетворять уравнению

поэтому

Таким образом, при n = 2 оптимальный фильтр формирует разность от импульса к импульсу при ρ₁ > 0 и сложение от импульса к импульсу при ρ₁ < 0.

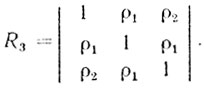(6.20)

Собственные значения удовлетворяют уравнению

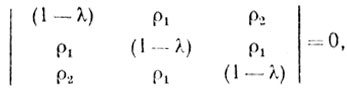
которое может быть записано в виде

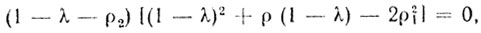
и, следовательно, собственные значения:

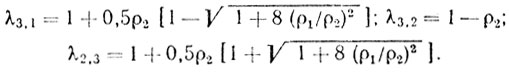
Составляющие собственного вектора U₃ удовлетворяют уравнениям:

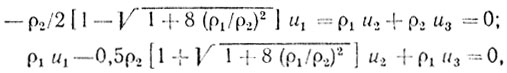
так что

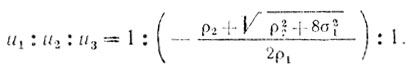(6.21)

Рассмотрим теперь на простых примерах, как можно использовать полученные результаты при определении параметров линейного режекторного фильтра.

Пусть S(t, φ) = A cos (ω_дt + φ), где ω_д - частота Доплера; φ - случайная начальная фаза, значения которой равномерно распределены в интервале 0 - 2π.

Очевидно, что

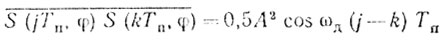(6.22)

и

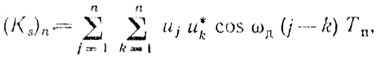(6.23)

если n = 2 и ρ₁ > 0, оптимальная весовая функция задается (6.18). Это соответствует схеме однократной ЧПК. Коэффициент K_sn(ω_д) = 1 - cos ω_дT_п.

Если n = 3 и 0 ≤ ρ₂ ≤ ρ₁ < 1, то оптимальные веса определяются соотношением (6.21). Если ρ₁ и ρ₂ близки к единице, то оптимальная схема обработки соответствует схеме двухкратной ЧПК с весами 1: -2: 1, для которой

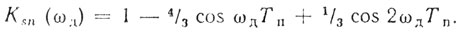
Выше отмечалось, то процедура оптимизации требует точного знания доплеровской частоты сигнала. Кроме того, рассматривалась, равномерная последовательность зондирующих импульсов. Теперь приведем решение задачи максимизации К_у с помощью оптимального выбора весовых коэффициентов для вобулированной последовательности импульсов при неизвестной доплеровской частоте.

Выражение для К_у(ω_д) можно записать следующим образом:

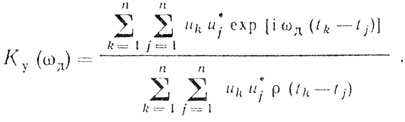(6.24)

Для данного частотного диапазона с граничными частотами f₁ и f₂

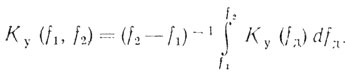(6.25)

Отметим, что

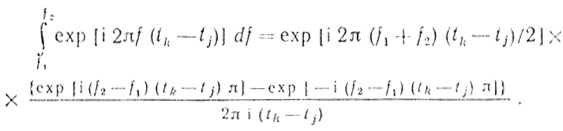(6.26)

Примем Δf = f₂ - f₁; f_cp = 0,5 (f₂ - f₁). Тогда выражение (6.25) приведем к виду

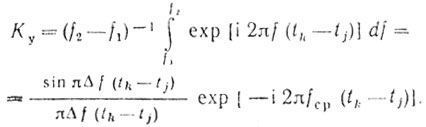(6.27)

И, наконец,

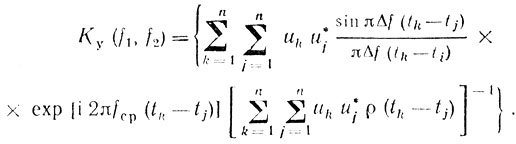(6.28)

Запишем (6.28) в матричной форме, для чего определим вектор-столбец

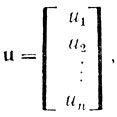(6.29)

а также матрицы В и R:

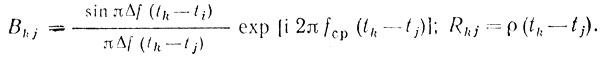(6.30)

Тогда

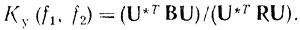(6.31)

Максимальное значение К_у(f₁, f₂) достигается при максимальном собственном значении матрицы R^-1B, а максимальное собственное значение достигается, когда U является собственным вектором, соответствующим наибольшему собственному значению.

Процедура определения оптимальных весов для каждого частотного диапазона может быть представлена следующим образом:

1. Определяются ширина полосы каждого диапазона Δf = f₂ - f₁ и среднее значение f_ср = 0,5 (f₁ + f₂).

2. Определяются моменты появления зондирующих им пульсов t_k.

3. Сопоставляется корреляционная матрица R размером n×n, элементы которой ρ(t_k - t_j).

4. Составляется корреляционная матрица В размером n×n, элементы которой определяются соотношением (6.30).

5. Составляется матрица произведения R^1_B.

6. Определяется наибольшее собственное значение произведения матриц R^-1B, а затем находится собственный вектор, соответствующий этому собственному значению. Собственный вектор является комплексным.

Указанная процедура повторяется для каждого из N частотных диапазонов. Максимальное количество частотных диапазонов задается соотношением

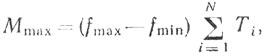(6.32)

где T_i - период следования импульсов. Ширина одного частотного диапазона

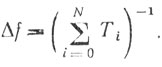(6.33)

Число и ширину частотных диапазонов необходимо определять с учетом необходимого значения коэффициента улучшения и объема аппаратурных затрат.