6.3. Оптимизация весовых коэффициентов режекторного фильтра СДЦ

Следуя [72, 74], рассмотрим задачу оптимизации весовых коэффициентов на примере наиболее распространенной схемы режекции нерекурсивного режекторного фильтра СДЦ когерентно-импульсной РЛС, излучающей пачку из n импульсов в моменты времени T₁, T₂, ..., Т_n. При этом для исключения "слепых" скоростей может происходить изменение периода от импульса к импульсу, однако минимальный межимпульсный период выбирается из условия однозначного определения дальности.

Запишем сигнал, отраженный от цели, в виде

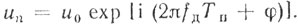(6.34)

Для оптимального обнаружения принимаемая пачка импульсов должна быть подвергнута весовой обработке: где оптимальные веса определяются соотношениями:

где b_ij - элементы корреляционной матрицы помех В. Собственные шумы приемника можно учитывать введением действительной постоянной величины, которая прибавляется к диагональному элементу корреляционной матрицы помехи. Выражение (6.35) определяет набор комплексных весовых коэффициентов нерекурсивного фильтра, структурная схема которого представлена на рис. 6.1. Весовые коэффициенты являются функциями частоты Доплера, поэтому требуются наборы фильтров для каждого канала.

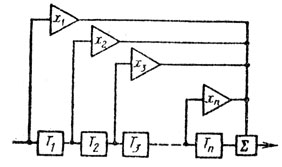
Рис. 6.1

Альтернативным подходом является разработка одного фильтрового канала с оптимизацией отношения сигнал-помеха для средней доплеровской частоты. Очевидно, что этот подход менее эффективен, но требует меньших аппаратурных затрат. Мощность сигнала на выходе такого одиночного фильтра

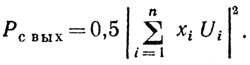(6.37)

Учитывая соотношение (6.34), это выражение можно представить в виде

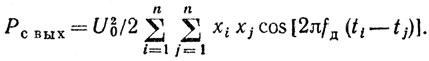(6.38)

Как показано в [72], Р_{с вых} является периодической функцией с частотой

где l_р - целые числа для i и j, а t_i и t_j должны быть рациональными числами. Частота f_p называется "слепой" (по аналогии со "слепой" скоростью). В случае когда доплеровская частота не известна, можно предположить, что она имеет равномерное распределение. Тогда

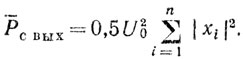(6.40)

Средняя мощность помехового сигнала на выходе

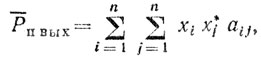(6.41)

где a_ij - элементы корреляционной матрицы помехи. При этом

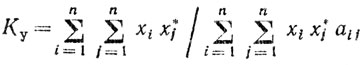(6.42)

и элементы корреляционной матрицы нормированы таким образом, что a_ij = 1.

Элементы a_ij корреляционной матрицы помехи определяются с помощью преобразования Фурье энергетического спектра пассивной помехи. Полагая это распределение нормальным, получаем

В случае использования регулярной зондирующей последовательности выражение (6.43) приводится к виду

где К = (i - j).

Сопоставление (6.43) и (6.44) показывает, что единственная разница в анализе СДЦ с вобуляцией периода повторения импульсов и без нее заключается в указанных элементах корреляционной матрицы. Заметим также, что эта матрица является симметричной, т. е. a_ij = а_ji. Ее диагональный элемент имеет вид

где η₀ - нормированный уровень собственных шумов.

На практике величиной η₀ обычно пренебрегают. Поскольку корреляционная матрица является действительной и симметричной, а весовые коэффициенты оптимального фильтра x_i являются составляющими собственного вектора этой матрицы, то, следовательно, x_i - действительные величины.

Величина Р_{п вых} определяется квадратичной формой, поэтому, представив весовые коэффициенты х₁, х₂, ..., x_N в виде N-мерного вектора х¯, можно записать

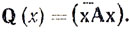(6.46)

Тогда выражение для К_у можно записать следующим образом:

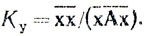(6.47)

Критерий оптимизации заключается в максимизации величины K_у или, что то же самое, в минимизации формы (хАх). Это равносильно решению хорошо известной задачи на нахождение собственного значения. Известно [72, 74], что собственные векторы и собственные значения обладают следующими свойствами:

собственные значения действительной симметричной матрицы являются действительными;

если матрица положительно определена, то и собственные значения являются положительными;

собственные векторы, находящиеся во взаимооднозначном соответствии с различными собственными значениями действительной симметричной матрицы, являются действительными и ортогональными.

С учетом последнего свойства квадратичная форма Q(х) может быть представлена как

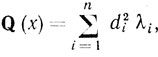(6.48)

где

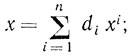(6.49)

λ_i - собственные значения; x - соответствующие собственные векторы.

Минимум Q(x) имеет место тогда, когда x¯ принимает значение собственного вектора, который соответствует минимальному собственному значению λ_min. Тогда Q(х) = λ_min. Таким образом, квадратичная форма имеет минимальную величину, которая равна наименьшему собственному значению матрицы А.

Если разложить детерминант |А - I|, то можно найти следующие соотношения между собственными значениями и элементами матрицы А:

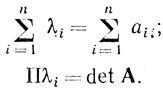(6.50)-(6.51)

Выше указывалось, что диагональные элементы матрицы А равны единице и поэтому

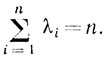(6.52)

Поскольку Q(х) положительно определена, то имеют место следующие соотношения [72]:

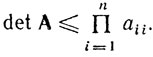(6.54)

Отсюда имеем

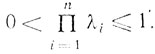(6.55)

Из (6.52) и (6.55) можно заключить, что

Здесь λ_min - наименьшее собственное значение, которое характеризует сигнал помехи на выходе оптимизированной схемы СДЦ.

Используя описанную выше процедуру оптимизации нерекурсивного режекторного фильтра для случая равномерной зондирующей последовательности, можно показать, что

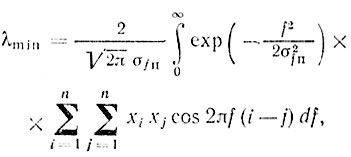(6.57)

где x_i - весовые коэффициенты оптимального нерекурсивного фильтра для данного значения σ_fп.

На рис. 6.2 приведены зависимости К_у от нормированного значения σ_fп. В качестве переменного параметра принято число импульсов в пачке n. Для значения n и σ_fп рассчитывается минимальное собственное значение. Величина, обратная собственному значению, равна К_у.

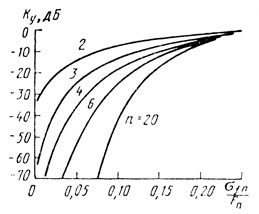
Рис. 6.2

Каждая из этих зависимостей представляет собой максимально достижимый коэффициент улучшения. Приведенные зависимости наглядно демонстрируют свойства полученных значений К_у. Все зависимости являются монотонными. Для конкретного значения σ_fп коэффициент улучшения стремится к пределу при увеличении числа обрабатываемых импульсов. По мере увеличения σ_fп все кривые сливаются в одну и коэффициент улучшения стремится к нулю.

Приведенные зависимости используют при разработке устройств СДЦ. Так, если σ_fпT_п = 0,1, то в случае, когда нерекурсивный фильтр обрабатывает 10 импульсов, можно ожидать, что К_у = 34 дБ. При дальнейшем росте n К_у практически не увеличивается.

Чтобы избежать появления "слепых" скоростей, обычно используют систему СДЦ с вобуляцией периода повторения. Период повторения может изменяться в широких пределах, что в значительной мере затрудняет анализ таких систем. Однако в реальных системах СДЦ область значений периода повторения в известной степени ограничивается такими параметрами, как время обзора и однозначно определяемая дальность. Это означает, что значения периодов повторения лежат между T_{п min}, определяемым однозначной дальностью, и T_{п max}, определяемым временем обзора:

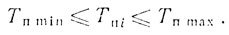(6.58)

Следовательно, можно предположить, что для минимального собственного значения, соответствующего периодам, удовлетворяющим соотношению (6.58), справедливо неравенство

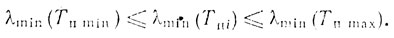(6.59)

На рис. 6.3 представлен типовой пример зависимости К_у от σ_fп/F_п для случая, когда нерекурсивный фильтр обрабатывает три импульса, а T_{п max} = 1,1T_{п min}. В этом случае значения К_у для σ_fпT_{п max} и σ_fпT_{п min} совпали. Однако естественно ожидать, что с увеличением диапазона значений периода повторения средняя эффективность анализируемой схемы СДЦ снизится.

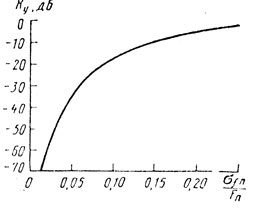
Рис. 6.3