6.4. Оптимизация системы СДЦ в условиях воздействия пассивных помех нескольких видов

Как правило, РЛС СДЦ работают в такой помеховой обстановке, когда наиболее вероятно наличие более одного вида пассивных помех. Например, помеховая обстановка может обусловливаться отражениями от подстилающей поверхности и от метеообразований. Эти два вида помех, как показано в гл. 3, могут иметь разные энергетические спектры, средние значения, дисперсии, даже если они описываются одним и тем же законом. Процедура оптимизации режекторного нерекурсивного фильтра при условии воздействия нескольких видов пассивных помех, как и в предыдущем случае, основывается на вычислении минимального собственного значения корреляционной матрицы помех. Элементы этой корреляционной матрицы, как показано в [73], зависят не только от вида энергетических спектров присутствующих видов помех, но и от средних значений ЭПР этих помех, а также от доплеровского сдвига между средними значениями частот спектров помех.

Предположим, что излучается равномерная последовательность зондирующих импульсов с периодом Т_п. Корреляционная функция определяется соотношением

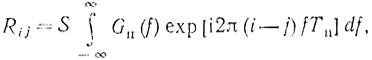(6.60)

где S - среднее значение ЭПР помехи.

Допустим, что отраженный сигнал содержит два вида помех. Эти помехи могут иметь различные энергетические спектры или при однотипных функциях плотности - различные дисперсии и средние доплеровские частоты. В любом случае предполагается, что отраженные сигналы от помех являются независимыми некоррелированными случайными процессами. С учетом сделанных предположений выражение (6.60) можно записать следующим образом:

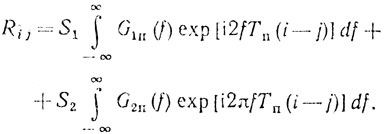(6.61)

Пусть излучается n импульсов, которые затем подвергаются весовой обработке с помощью весовых коэффициентов u_i и суммируются. Сигнал помехи на выходе такого фильтра имеет вид

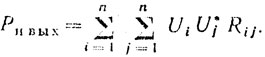(6.60)

Предположим, что доплеровские частоты распределены равномерно. Тогда мощность сигнала на выходе фильтра

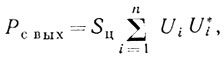(6.63)

где S_ц - среднее значение ЭПР цели.

Отношение сигнал-помеха на входе фильтра

Коэффициент улучшения с учетом (6.62)-(6.64) записывается следующим образом:

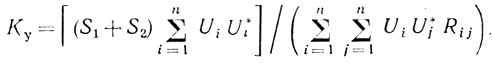(6.65)

Аналогичные рассуждения распространяются и на случай, когда число видов помех больше двух, при условии, что помехи представляют собой независимые и некоррелированные случайные процессы.

Для удобства дальнейших расчетов проведем нормировку весовых функций [72]:

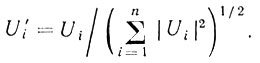(6.66)

Целесообразно нормировать также корреляционные функции с помощью соотношения

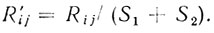(6.67)

Тогда формула для вычисления коэффициента улучшения примет вид

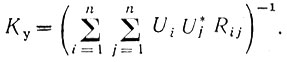(6.68)

В этом случае оптимизация сводится к нахождению такого множества весовых коэффициентов u_i, чтобы квадратичная форма

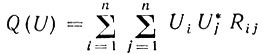(6.69)

была бы минимальной при условии, что

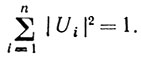(6.70)

Для двух помех корреляционная функция может быть представлена в вид

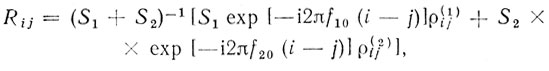(6.71)

где

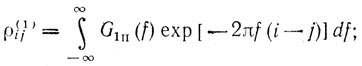
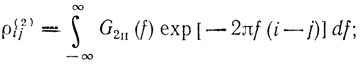
f = f_д/F_п - нормированная частота Доплера; f₁₀ и f₂₀ - соответственно средние доплеровские частоты спектров первого и второго видов помех.

Положим, что:

Тогда соотношение (6.71) преобразуется к виду

Если принять, что u'₁ - u_i exp (-2πf₀i), то квадратичная форма (6.69) запишется следующим образом:

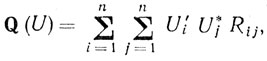(6.73)

где

Замена u_i на u'_i по-прежнему не исключает условия нормировки, т. е.

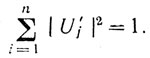
Таким образом, проблема оптимизации системы СДЦ, работающей в условиях воздействия пассивных помех нескольких видов, сводится к нахождению весовых коэффициентов U'_i, минимизирующих квадратичную форму (6.73). Такая задача эквивалентна определению минимального собственного вектора корреляционной матрицы R, состоящей из элементов R_ij. Соответствующие компоненты такого вектора могут быть использованы как весовые коэффициенты фильтра.

Заметим, что R_ij = 1, R_ij = R*_ij. Следовательно, матрица R является эрмитовой, а ее элементы - функциями, зависящими от G_1п(f) и G_2п(f), от отношения средних ЭПР двух помех, т. е. величины Р, и от частоты f₀, которая является доплеровским сдвигом между средними доплеровскими частотами энергетических спектров двух видов помех.

Для упрощения предположим, что разность средних доплеровских частот равна нулю, т. е. f₀ = 0. Тогда элементы корреляционной матрицы

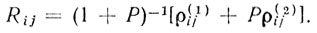(6.75)

Минимальное собственное значение матрицы R может быть представлено в виде

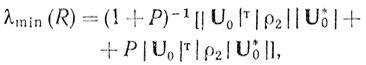(6.76)

где |u₀| - собственный вектор, связанный с минимальным собственным значением матрицы R. Матрицы ρ₁ и ρ₂ представляют собой корреляционные матрицы для отдельных видов помех. Все матрицы положительно определены. Следовательно, минимальные собственные значения таких матриц также будут положительны. Существует только один вектор в N-мерном пространстве, который соответствует этому минимальному собственному значению. Вектор |u₀| не обязательно является этим минимальным собственным вектором.

Можно записать:

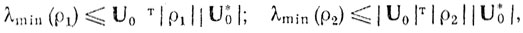
и, таким образом,

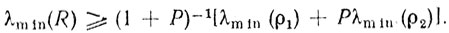(6.77)

Равенство имеет место только тогда, когда минимальные собственные векторы матриц R, ρ₁ и ρ₂ идентичны. Уравнение (6.77) может быть записано следующим образом:

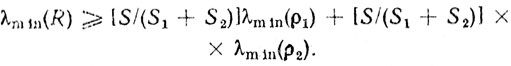(6.78)

Уравнение (6.78) довольно просто обобщается на случай большого числа видов помех:

Величина λ_min(R) характеризует минимальный помеховый сигнал на выходе устройства СДЦ в условиях воздействия пассивных помех различных видов, в то время как λ_min(ρ₁), λ_min(ρ₂), ... λ_min(ρ_k) характеризуют соответственно минимальные помеховые сигналы отдельных помех. Сумма в правой части уравнения (6.79) представляет собой среднее взвешенное сигналов помехи на выходе системы СДЦ, полученных при условии оптимизации схемы режекции для определенного вида пассивной помехи. Весовые коэффициенты определяются средними значениями ЭПР помех S₁, S₂, ..., S_k. Еще раз напомним, что уравнение (6.79) справедливо в том случае, когда сигналы от различных видов помех являются независимыми случайными процессами. На вид энергетического спектра ограничений не налагается.

На рис. 6.4 и 6.5 представлены некоторые количественные результаты для случая двух помех [73]. Функции энергетического спектра обоих видов помех предполагаются гауссовскими. Параметр σ_fп нормируется относительно F_п. Для помехи первого типа σ_fп1 Т = 0,01, для второго типа ρ_fп2 Т_п = 0,1. Коэффициент улучшения оптимальной схемы СДЦ определялся в зависимости от отношения ЭПР двух видов помех. Из рис. 6.4, 6.5 следует, что K_у увеличивается с увеличением ρ. Видно также, что в общем случае наличие доплеровского сдвига между средними частотами энергетических спектров помех приводит к снижению коэффициента улучшения.

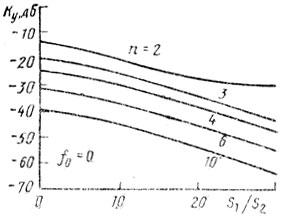
Рис. 6.4

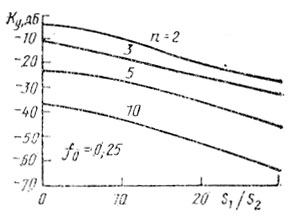
Рис. 6.5

На рис. 6.6 и 6.7 приведены зависимости коэффициента улучшения от доплеровского сдвига между средними частотами спектров помех, из которых следует, что наибольшее значение К_у имеет место при нулевом сдвиге доплеровских частот. Рост числа обрабатываемых импульсов обычно повышает эффективность работы системы СДЦ.

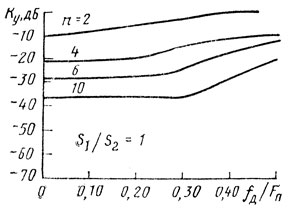
Рис. 6.6

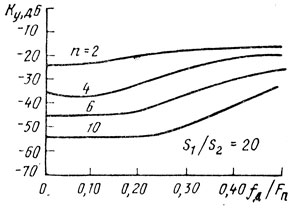
Рис. 6.7