Приложение. Методы коррекции квадратурных каналов

В гл. 5 показано, что в цифровых системах СДЦ при обработке поступающих сигналов используются квадратурные каналы (см. рис. 5.14). Анализ работы таких систем обычно проводится при условии ортогональности каналов и их полной идентичности. Однако такие условия, как правило, не выполняются, поэтому на практике получают более низкие по сравнению с расчетными параметры эффективности. В гл. 9 приведено соотношение для расчета К_у при амплитудных и фазовых рассогласованиях квадратурных каналов, в работах [103-105] показано, что разбаланс между указанными каналами на 0,1 дБ и по фазе (имеются в виду опорные сигналы, подаваемые на фазовые детекторы от когерентного гетеродина) на 1° не позволяет подавлять сигналы помехи больше чем на 40 дБ. Помимо амплитудного и фазового рассогласований квадратурных каналов, способствующих формированию паразитных компонент на частоте зеркального канала, существуют так называемые ошибки смещения [105], возникающие из-за наличия постоянных составляющих напряжения в фазовых детекторах, усилителях звуковой частоты, АЦП. Ошибки смещения являются причиной формирования паразитного сигнала на нулевой частоте Доплера. В том случае, когда пассивная помеха формируется в результате отражения от поверхности земли, указанная паразитная составляющая подавляется режекторным фильтром. Если же источник пассивной помехи перемещается с определенной скоростью (гидрометеоры, облака диполей), а система СДЦ адаптивна по отношению к центру энергетического спектра пассивной помехи, наличие паразитного сигнала, возникающего из-за ошибок смещения, может привести к резкому снижению эффективности.

Таким образом, для обеспечения высокоэффективной работы цифровых систем СДЦ необходимо решать задачу коррекции квадратурных каналов.

Определим поправочные коэффициенты при условии ортогональности сигналов двух квадратурных каналов на выходе АЦП [104]. Обозначим их

где Δ и φ - амплитудный и фазовый разбаланс соответственно; a и b - ошибки смещения в каналах I и Q.

Аддитивный характер ошибок смещения позволяет достаточно просто их компенсировать при наличии оценки a и b для каждого канала.

С учетом компенсации ошибок смещения соотношения (П.1) и (П.2) можно представить в виде

Процедура коррекции амплитудных и фазовых ошибок аналогична процедуре ортогонализации Грам-Шмидта [104, 106]. Сигналы I₂ и Q₂ можно рассматривать как векторы, а соответствующие коэффициенты коррекции G_Δ и G_φ должны обеспечить пересчет одного вектора и поворот другого. Обозначив через I₃ и Q₃ сигналы квадратурных классов после коррекции, процедуру ортогонализации в матричной форме можно записать следующим образом:

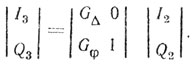(П.5)

Решение уравнений (П.5) дает следующие значения коэффициентов коррекции [104]:

и сигналов:

Из (П.8) и (П.9) видно, что сигналы I₃(t) и Q₃(t) ортогональны и имеют равные амплитуды. Амплитудный множитель cos φ, образовавшийся в результате процедуры коррекции не влияет на значения I₃(t) и Q₃(t), если φ не превышает 0,1 рад.

На практике коэффициенты коррекции целесообразно формировать с помощью дискретного преобразования Фурье тест-сигнала, который можно представить в виде:

где θ - случайная фаза.

Как показано в [104] для получения коэффициентов коррекции достаточно сформировать четыре выборки дискретного преобразования Фурье, определяемого соотношением:

где k = 0, 1, 2, ..., N - 1; N - число выборок; f(nТ) - временные выборки тест-сигнала; 1/Т - частота временной дискретизации.

С учетом соотношений (П.10) и (П.11) можно записать:

Учитывая, что частотная характеристика ДПФ представляется набором узкополосных фильтров, коэффициенты компенсации ошибок смещения определяются из соотношения

а коэффициенты компенсации амплитудных и фазовых ошибок из соотношения

где F(1/NT) - 0,5 А [(1 + Δ) + cos φ + i sin φ] exp(iθ) - выход ной сигнал фильтра тест-сигнала;

F(3/NT) = 0,5 A [(1 + Δ) - cos φ + i sin φ] exp(iθ) - выходной сигнал фильтра зеркального канала тест-сигнала; F*(1/NT) - комплексно сопряженная F(1/NT).

Учитывая (П.6), (П.7) и (П.13), можно записать:

Коэффициенты коррекции могут быть выражены непосредственно через выборки тест-сигнала с помощью алгоритма 4-точечного ДПФ:

где

х0 = (1 + Δ) A cos θ + а,     y0 = A sin (θ + φ) + b, 
х1 = -(1 + Δ) A sin θ + а,    y1 = A cos (θ + φ) + b, 
х2 = -(1 + Δ) A cos θ + а,    y2 = -A sin (θ + φ) + b, 
х3 = (1 + Δ) A sin θ + а,     y3 = -A cos (θ + φ) + b.

В заключение отметим, что процедура коррекции квадратурных каналов из-за наличия собственных шумов не обеспечивает их идеальной ортогональности.

Точность описанной процедуры можно оценить с помощью дисперсии коррекции, которая для амплитудных и фазовых ошибок определяется

для ошибок смещения

где σ² = A²/2q; А - амплитуда тест-сигнала; q - отношение сигнал-шум для тест-сигнала.