4.8. Колебание, модулированное по фазе случайным процессом. Плотность вероятности

Модулированное колебание представим в форме

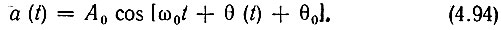
Как и в предыдущем параграфе, зададим нормальное вероятностное распределение модулирующей функции s(t) [см. (4.84)].

При линейной характеристике фазового модулятора с крутизной k_фм [рад/В] мгновенное значение фазы определяется выражением

а плотность вероятности случайной величины θ выражением

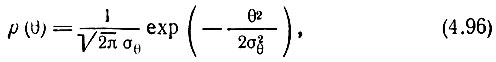
где

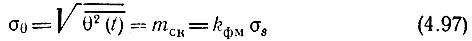
можно рассматривать как среднеквадратическое значение индекса угловой модуляции.

Заметим, что при гармонической модуляции фазы по закону θ(t) = m sin Ωt, очевидно,

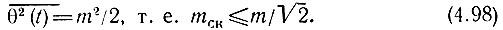
При определении плотности вероятности функции а(t) следует различать два случая: а) детерминированная начальная фаза θ₀; б) случайная начальная фаза θ₀.

Остановимся на рассмотрении первого случая. При измерении напряжения а(t) в какой-либо фиксированной момент времени t₁ значение а(t) отличается от детерминированного значения A₀ cos (ω₀t + θ₀) только из-за наличия случайного фазового сдвига θ, обусловленного модуляцией. Задание плотности вероятности θ позволяет найти плотность вероятности а с помощью рассуждений, использованных при выводе формулы (4.25). Отличие заключается лишь в том, что в рассматриваемой задаче величина θ не ограничена интервалом (-π, π) и, кроме того, неравновероятна в любом интервале.

При подсчете вероятности пребывания а(t) в заданном интервале (а, а + da) следует учитывать все фазовые интервалы, в которых плотность вероятности р(θ) отлична от нуля. Так, например, если начальная фаза θ₀ = 0, расположение этих интервалов соответствует указанному на рис. 4.21. В этом частном случае плотность вероятности р(а) (по аналогии с (4.25) и с учетом (4.96)) принимает следующий вид:

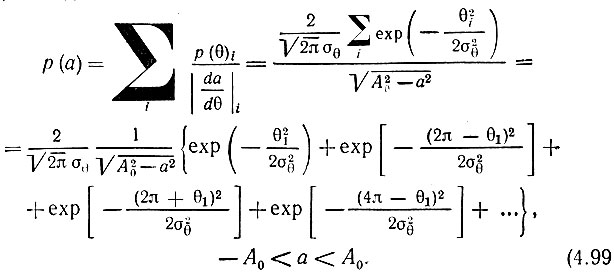
В этом выражении θ₁ = arccos (а/А₀), причем 0 ≤ |θ₁| ≤ π. Число существенных слагаемых в (4.99) зависит от среднеквадратического значения индекса угловой модуляции σ_θ. При относительно малых значениях σ_θ, не превышающих 1-2 рад, можно ограничиться первым слагаемым. Графики р(а) при нескольких значениях σ_θ представлены на рис. 4.22.

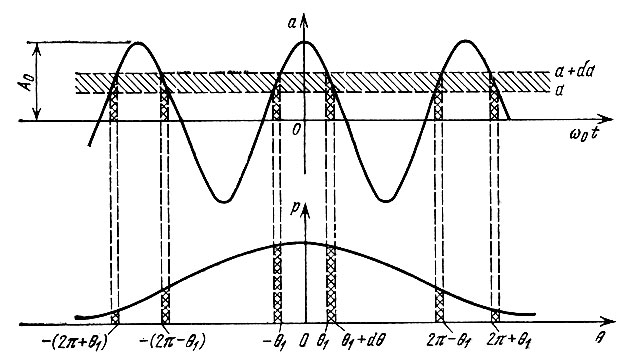
Рис. 4.21. К определению плотности вероятности высокочастотного колебания при модуляции фазы случайным процессом

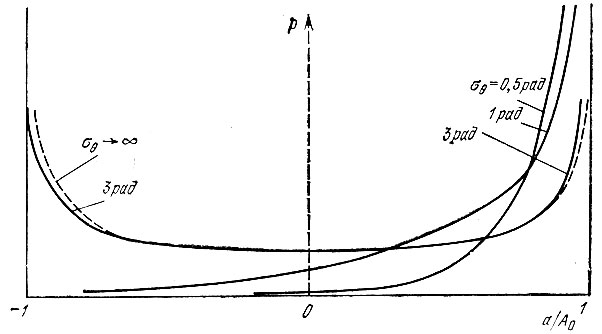
Рис. 4.22. Плотность вероятности высокочастотного колебания при модуляции фазы случайным процессом

Видно, что при σ_θ → 0 распределение приближается к р(а) → δ(а - А₀), что соответствует 100%-ной вероятности амплитудного значения а(t) в момент t = 0. При относительно больших значениях σ_θ (свыше 3 рад) распределение случайной величины а мало отличается от распределения, соответствующего гармоническому колебанию с равновероятной в интервале (0, 2π) фазой. График р(а) в этом случае почти совпадаете графиком, построенным по формуле (4.25) (штриховая кривая).

Существенно иная картина получается в случае, когда начальная фаза колебания θ₀ (в отсутствие модуляции) равна π/2. Соотношение между интервалами значений а(t), соответствующими им фазовыми интервалами и плотностью вероятности р(θ) представлено на рис. 4.23, При θ₀ = π/2 формула, аналогичная (4.99), принимает вид

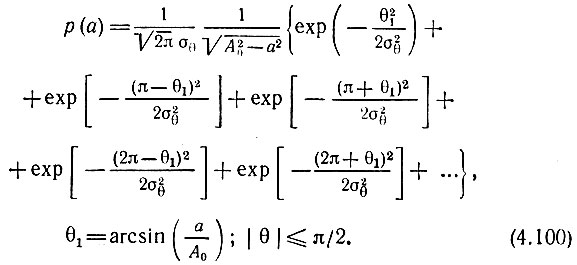
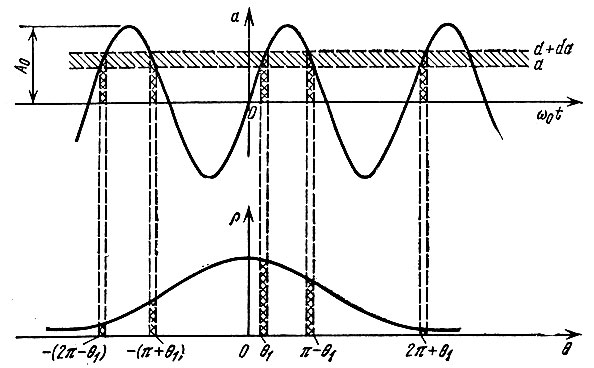
Рис. 4.23. То же, что на рис. 4.21, но при иной начальной фазе несущего колебания

Графики р(а) при нескольких значениях σ_θ представлены на рис. 4.24.

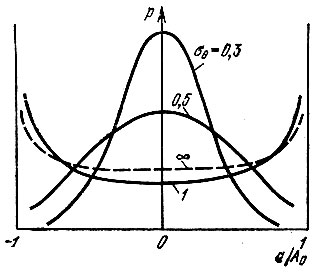
Рис. 4.24. То же, что на рис. 4.22, но при иной начальной фазе несущего колебания

При малых значениях σ_θ распределение a(t) приближается к нормальному, а при больших - к распределению (4.25).

Из сопоставления двух характерных режимов θ₀ = 0 и θ₀ = π/2 видно, что плотность вероятности р(а) зависит от начальной фазы или, что то же, от момента отсчета t₁. Таким образом, при детерминированной начальной фазе θ₀ a(t) является нестационарным процессом. Можно, однако, отметить, что с увеличением σ_θ влияние θ₀ на р(а) ослабевает. При достаточно больших σ_θ процесс приближается к стационарному.

Закон распределения а(t) при фазовой модуляции и случайной начальной фазе θ₀ здесь не рассматривается. Отметим лишь, что при достаточно медленной модуляции, отвечающей условию (3.3), т. е. когда колебание а(t) сохраняет форму, близкую к гармоническому колебанию, плотность вероятности р(а) совпадает с (4.25).

Корреляционная функция и энергетический спектр при угловой модуляции случайным процессом здесь не рассматриваются (см. [6]).