4.7. Колебание, модулированное по амплитуде случайным процессом

Вернемся к выражению (3.4) и рассмотрим его с вероятностной точки зрения, учитывая, что передаваемое сообщение содержится в огибающей А(t).

Пусть огибающая A(t) - стационарный, эргодический случайный процесс. Связь между изменением огибающей и модулирующей функцией s(t) определяется, как и в § 3.2, соотношением ΔA(t) = k_ам s(t), где k_ам имеет смысл крутизны характеристики амплитудного модулятора.

Закон распределения вероятностей передаваемого сообщения зададим нормальным с нулевым средним. Таким образом, плотность вероятности величины s(t)

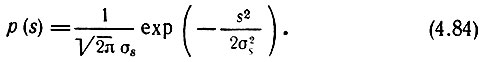
Соответственно и плотность вероятности огибающей А при линейной модуляции может быть принята нормальной:

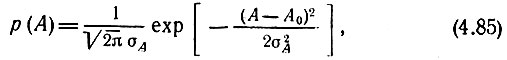
где σ_А = k_ам σ_s.

Выражение (4.85) справедливо и имеет смысл, если среднеквадратическое значение глубины модуляции не настолько велико, чтобы проявлялось ограничение огибающей при модуляции вниз. Под среднеквадратической глубиной модуляции в данном случае можно подразумевать^* отношение М_ск = σ_А/А₀. Нужно, чтобы вероятность уменьшения A(t) до нулевого значения была пренебрежимо мала. Это требование выполняется, если М_ск ≤ 0,3-0,4 (см. § 4.2, п. 4), т. е. если ширина шумовой дорожки (по огибающей), равная ∼ 5σ_А, не превышает удвоенной амплитуды А₀. Примерный вид одной из реализаций модулированного колебания а(t), соответствующего поставленному условию, изображен на рис. 4.19.

^* (Заметим, что при модуляции по гармоническому закону A(t) = A×(1 + M cos Ωt) среднеквадратическое значение М_ск определяется из соотношения 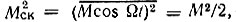откуда )

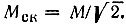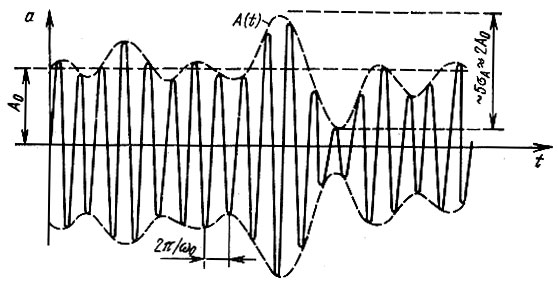
Рис. 4.19. Примерный вид высокочастотного колебания, модулированного по амплитуде нормальным случайным процессом

Выберем произвольный момент времени t = t₁ и запишем для этого момента выражение (3.4):

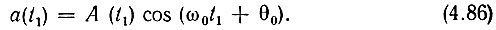
Умножение случайной величины А(t₁) с одномерной плотностью р(A) (не зависящей от выбора момента времени) на детерминированный множитель cos(ωt₁ + θ₀) приводит к изменению математического ожидания и дисперсии в зависимости от выбора t₁. Случайный процесс а(t), определяемый выражением (4.86), остается нормальным, но нестационарным, а следовательно, и неэргодическим (см. § 4.2, п. 2, где рассматривался аналогичный случайный процесс, но при ином распределении огибающей).

Для полного описания случайного процесса a(t) найдем его корреляционную функцию и энергетический спектр. Поскольку процесс нестационарен, корреляционная функция зависит не только от интервала τ, но и от времени t:

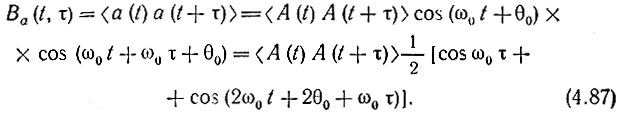
Так как А(t) - стационарный процесс, то первый множитель в (4.87)

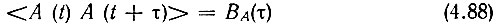
представляет собой корреляционную функцию огибающей А(τ), не зависящую от t.

Зависящая от t величина cos (2ω₀t + 2θ₀ + ω₀τ) является быстроосциллирующей (с частотой 2ω₀) функцией. В подобных случаях вводят усредненную по времени корреляционную функцию

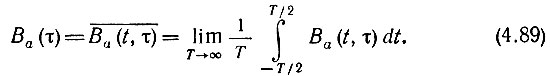
При таком усреднении слагаемое cos (2ω₀t + 2θ₀ + ω₀τ) в (4.87) можно отбросить. Таким образом, в рассматриваемом примере

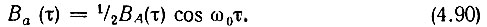
Этот результат совпадает с выражением (3.103), выведенным для детерминированного колебания. Отличие заключается лишь в способе определения В_А(τ). В § 3.11 В_А(0) имело размерность энергии, а в данном случае В_А(0) имеет смысл средней мощности случайного процесса.

Применяя выражение (4.38) к усредненной по времени функции В_а(τ), находим энергетический спектр модулированного колебания:

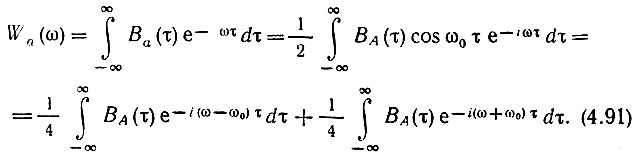
Учитывая, что среднее значение А(t) равно A₀, представим В_A(τ) в форме выражения (4.18), заменив в нем х‾ на A₀, ρ_x(τ) на ρ_A(τ) и В_х(τ) на В_А(τ):

где ρ_A(τ) - ковариационная функция огибающей.

Подставив (4.92) в (4.91) и учтя выражение (2.94'), получим

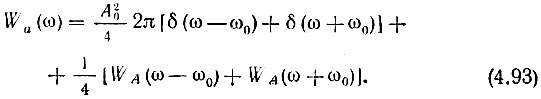
В этом выражении W_A(ω - ω₀) = W_А(Ω) - энергетический спектр флуктуационной части огибающей А(t), связанный с энергетическим спектром W_s(Ω) модулирующей функции s(t) очевидным соотношением W_А(Ω) = k²_амW_s(Ω). Связь между W_А(Ω) и W_a(ω) иллюстрируется рис. 4.20.

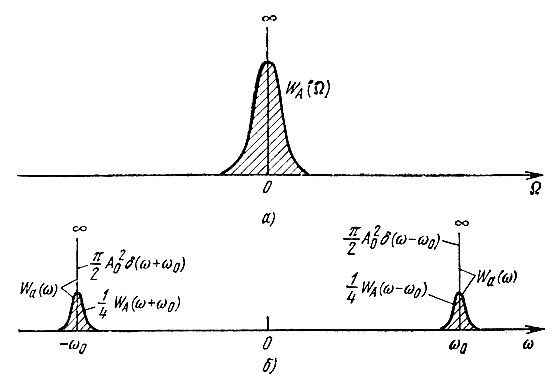
Рис. 4.20. Энергетические спектры: а - огибающей амплитуд при модуляции нормальным случайным процессом; б - мгновенного значения модулированного колебания