
4.6. Узкополосный случайный процесс
Краткое описание свойств нормального шума, сформированного из белого шума вырезанием относительно узкой полосы частот, было дано в § 4.4. Там, отмечалось, что каждая из реализаций подобного случайного процесса имеет вид почти гармонического колебания
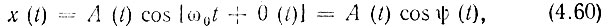
все параметры которого - огибающая А(t), фаза θ(t) и частота ω(t) - являются случайными, медленно меняющимися функциями времени.
При представлении шума в форме (4.60) предполагается, что огибающая А(t) отвечает соотношению
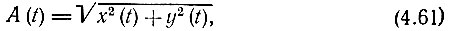
где y(t) - функция, сопряженная по Гильберту исходной функции х(t) (см. § 3.9), а ω0 выбрана таким образом, что не содержит слагаемого, линейно зависящего от t.
Дальнейшее рассмотрение основано на допущении, что энергетический спектр шума х(t) сконцентрирован в узкой по сравнению с величиной ω0 полосе, причем функция Wx(ω) в указанной полосе симметрична относительно точки ω0 (рис. 4.13, а).
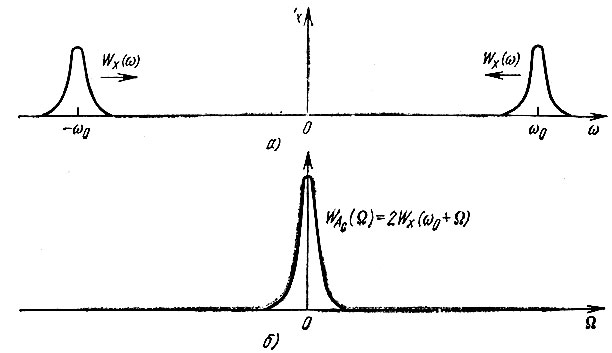
Рис. 4.13. Энергетические спектры: а - узкополосного процесса с центральной частотой ω0; б - косинусной составляющей комплексной огибающей
Рассмотрим стационарный эргодический процесс с нормальным законом распределения вероятностей. Здесь необходимо подчеркнуть, что указанное распределение характеризует физическое колебание х(t), т. е. мгновенное значение колебания (в любой момент времени t). Параметры же колебания: А(t), θ(t) и ω(t) = dψ/dt - обладают законами распределения, существенно отличающимися от нормального*. Для полного описания свойств узкополосного процесса требуется знание законов распределения, а также корреляционных функций всех, параметров колебания.
* (Это вытекает из нелинейного характера зависимости параметров А, θ и ω от x и y.)
1. Огибающая
Представим высокочастотное колебание х(t), определяемое выражением (4.60), в виде суммы двух квадратурных колебаний:
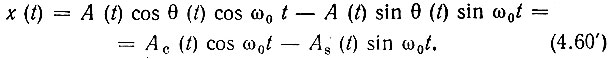
Здесь, как и в § 3.5,
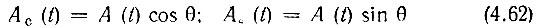
представляют собой амплитуды соответственно косинусной и синусной составляющих колебания х(t), причем
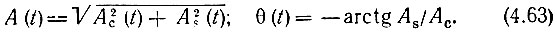
Для отыскания плотности вероятности рА(А) и рθ(θ) требуется знание соответствующих плотностей р(Ас) и р(As), а также совместной плотности вероятности р(Ас, As).
Плотности р(Aс) и р(As) можно определить, сопоставив случайную функцию Ас(t) [или Аs(t)] с функцией х(t):
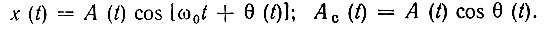
Отличие Ас(t) от х(t) заключается в исключении слагаемого ω0t из аргумента косинуса. Как и в случае детерминированного колебания, это означает сдвиг спектра каждой из реализаций случайного процесса на величину ω0 (в направлении к нулевой частоте, при сохранении структуры спектра). При этом сохраняется и закон распределения случайной функции х(t). Поэтому, если процесс х(t) нормальный, то и процесс Ас(t) нормальный (оба процесса с нулевым средним).
Энергетический спектр WAc(Ω) случайной функции Ас(t) можно получить из энергетического спектра функции х(t) сдвигом на ω0 левого лепестка и на - ω0 правого лепестка спектра Wx(ω) (рис. 4.13).
В результате получается энергетический спектр
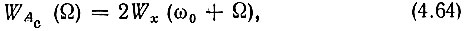
группирующийся вблизи нулевой частоты. Коэффициент 2 учитывает* сложение мощностей, приходящихся на оба лепестка Wx(ω).
* (В случае детерминированного АМ колебания (рис.3.9) при переходе от спектра Sa(ω) к спектру SА(ω) удваивается спектральная плотность напряжения (или тока), что приводит к учетверению спектральной плотности энергии, пропорциональной SА2(ω). В данном случае мощность всего лишь удваивается из-за некогерентного суммирования энергетических спектров от обоих лепестков Wx(ω).)
Аналогичные рассуждения используем для случайного процесса As(t) и его энергетического спектра
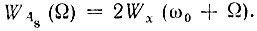
Из этого выражения и рис. 4.13 вытекает, что площадь под кривой Wx(ω) (в двух лепестках) совпадает с площадью под кривой 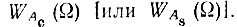 Следовательно, дисперсии случайных функций Ас(t), Аc2(t) и х(t) одинаковы:
Следовательно, дисперсии случайных функций Ас(t), Аc2(t) и х(t) одинаковы: 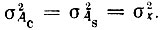
При учете первого выражения (4.63), из которого вытекает равенство 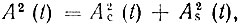 приходим к следующему выражению для среднего квадрата огибающей:
приходим к следующему выражению для среднего квадрата огибающей:
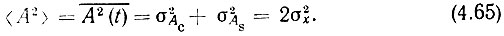
Итак, одномерные плотности вероятности случайных функций Ас(t) и As(t) можно определить выражениями
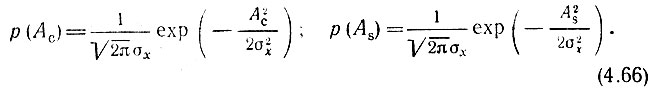
Кроме того, взаимная корреляция между функциями Ас(t) и As(t) равна нулю при τ = 0. Действительно, возводя выражение (4.60') в квадрат и усредняя по множеству, получаем
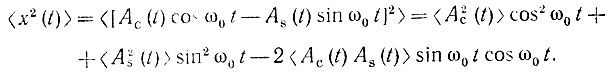
Но левая часть этого выражения равна 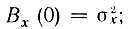 кроме того,
кроме того, 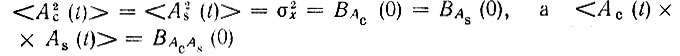 является взаимнокорреляционной функцией случайных процессов Ас(t) и As(t) при τ = 0. Следовательно, предыдущее равенство приводится к виду
является взаимнокорреляционной функцией случайных процессов Ас(t) и As(t) при τ = 0. Следовательно, предыдущее равенство приводится к виду
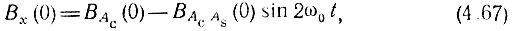
из которого вытекает, что BAcAs(0) = 0 [поскольку процессы х(t) и Ас(t) стационарны, равенство (4.67) должно выполняться в любой момент времени].
Итак, Ас(t) и As(t), отсчитываемые в один и тот же момент времени, - независимые величины*. Поэтому совместную плотность вероятности р(Ac, As) можно определить выражением
* (Это положение вытекает также из соотношения (4.65), показывающего, что средний квадрат огибающей А(t), т. е. σА2, является аддитивной суммой средних квадратов функций Ас(t) и As(t).)
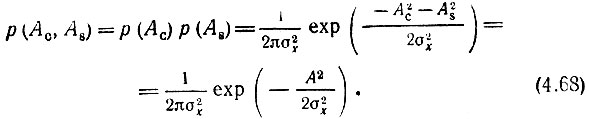
Вероятность того, что конец вектора A(t) лежит в элементарном прямоугольнике dAcdAs (рис. 4.14) равна произведению вероятностей пребывания Ас в интервале dAc и As в интервале dAs:
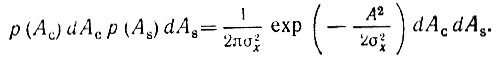
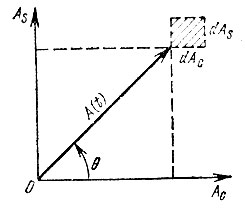
Рис. 4.14. К определению двумерной плотности вероятности квадратурных составляющих комплексной огибающей узкополосного процесса
При переходе от прямоугольных координат к полярным площадь заштрихованного на рис. 4.15 элемента будет AdθdA, а вероятность пребывания конца вектора в этом элементе равна
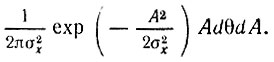
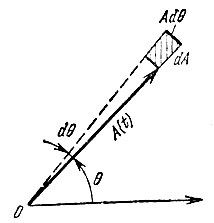
Рис. 4.15. К определению двумерной плотности вероятностей модуля и аргумента комплексной огибающей
Из этого выражения следует, что двумерная плотность
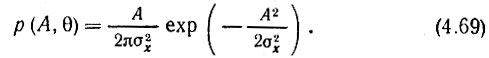
Интегрируя по переменной θ, получаем одномерную плотность
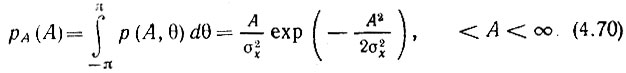
Обоснование пределов интеграла приводится в следующем пункте данного параграфа.
Распределение огибающей, характеризуемое этой плотностью вероятности, называется распределением Релея (рис. 4.16). Максимальное значение функции рА(А) получается при А = σх. Это означает, что А = σх является наивероятнейшим значением огибающей.
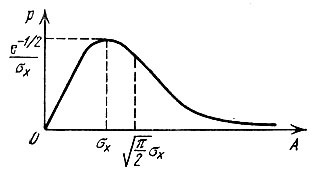
Рис. 4.16. Плотность вероятности релеевского распределения
Среднее же значение (математическое ожидание) огибающей
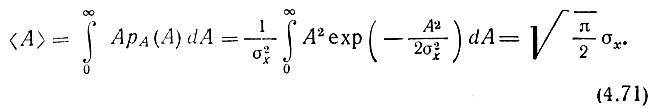
Аналогично средний квадрат огибающей
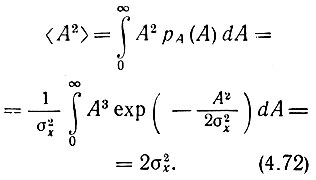
Этот результат совпадает с (4.65).
Таким образом, средняя мощность огибающей равна удвоенной дисперсии шума. Это аналогично соотношению между квадратом амплитуды А0 и средней мощностью гармонического колебания a(t) = А0cos ω0t, равной 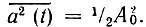
Вероятность того, что огибающая A(t) превысит некоторый заданный уровень С, определяется формулой
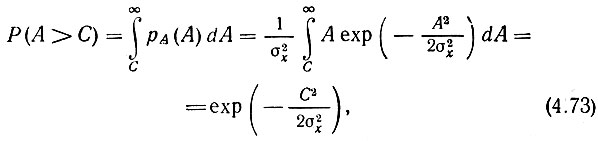
а вероятность того, что огибающая A(t) будет ниже уровня С, - формулой
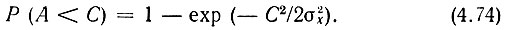
Из этих формул видно, что уже при 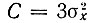 вероятность превышения уровня С составляет всего лишь ~1%. Поэтому можно считать, что ширина шумовой дорожки, фактически наблюдаемой, например, на экране осциллографа (рис. 4.17), не превышает (5-6) σх.
вероятность превышения уровня С составляет всего лишь ~1%. Поэтому можно считать, что ширина шумовой дорожки, фактически наблюдаемой, например, на экране осциллографа (рис. 4.17), не превышает (5-6) σх.
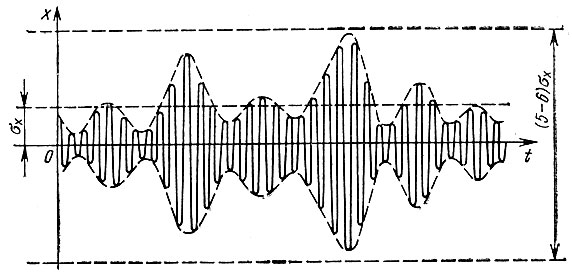
Рис. 4.17. Ширина шумовой дорожки узкополосного нормального шума при вероятности превышения границ ~1%
Этот результат, естественно, близок к данным, приведенным в § 4.2 для шумовой дорожки широкополосного нормального процесса (со спектром примыкающим к нулевой частоте).
Корреляционная функция огибающей узкополосного нормального шума [6] определяется по формуле, которую приводим без вывода:
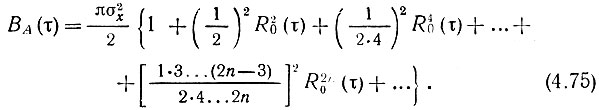
Здесь R0(τ) представляет собой огибающую нормированной корреляционной функции шума х(t), т. е. функции, определяемой выражением (при 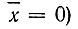
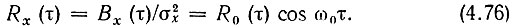
Так как R0 ≤ 1, то ряд (4.75) быстро сходится. Поэтому можно ограничиться первыми двумя членами:
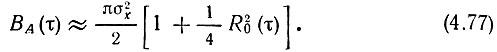
Применяя к ВА(τ) преобразование Фурье [см. (4.38)], находим энергетический спектр огибающей
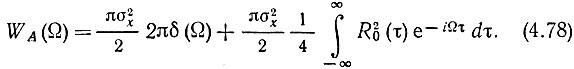
Из выражения (4.78) видно, что энергетический спектр огибающей примыкает к нулевой частоте. Первое слагаемое в правой части (4.78) соответствует постоянной составляющей огибающей, а второе - сплошной части спектра.
Примеры применения формул (4.75)-(4.78) приводятся в § 11.3-11.5.
2. Фаза
Интегрирование двумерной плотности р(А, θ), определяемой выражением (4.69), по переменной А дает одномерную плотность вероятности фазы
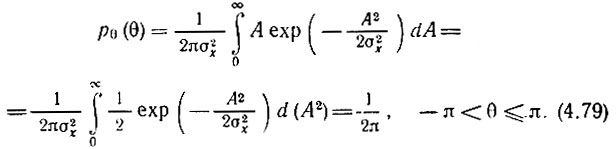
Этот результат согласуется с пределами интегрирования в (4.70).
Заметим, что из представления р(A, θ) [см. (4.69)] в виде произведения
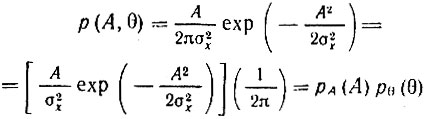
непосредственно вытекает независимость случайных величин A и θ. Как и в отношении Aс(t) и As(t), это справедливо при отсчете A(t) и θ(t) в один и тот же момент времени [см. замечание к (4.67)].
Соотношения (4.70) и (4.79) позволяют сделать следующее общее заключение: произведение вида х = A cos θ, в котором A и θ - независимые случайные величины, причем A распределена по Релею, а θ - равновероятна в интервале (-π, π), обладает нормальной плотностью вероятности.
Условие узкополосности процесса х(t) не обязательно; необходимо лишь, чтобы A и θ были связаны соотношениями (4.63).
Корреляционная функция фазы θ(t) определяется выражением [6]
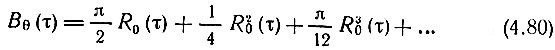
При τ = 0 ряд сходится к π2/3, т. е. дисперсия фазы равна π2/3. Действительно, при распределении (4.79)
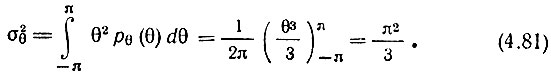
3. Частота
Основываясь на выражении (4.60), мгновенную частоту шума можно записать в форме
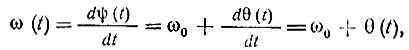
откуда видно, что закон распределения мгновенной частоты определяется распределением производной фазы θ.
Приведем без вывода [6, 7] выражение для плотности вероятности случайной величины θ
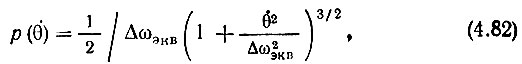
где Δωэкв - эквивалентная ширина спектра узкополосного процесса, определяемая выражением
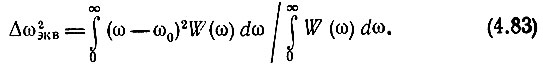
Последнее выражение эквивалентно формуле
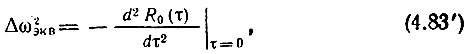
где R0(τ) - огибающая нормированной корреляционной функции процесса, обладающего энергетическим спектром W(ω) [симметричным относительно центральной частоты ω0].
График функции 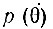 изображен на рис. 4.18. Среднее значение абсолютной величины
изображен на рис. 4.18. Среднее значение абсолютной величины 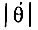 равно Δωэкв.
равно Δωэкв.
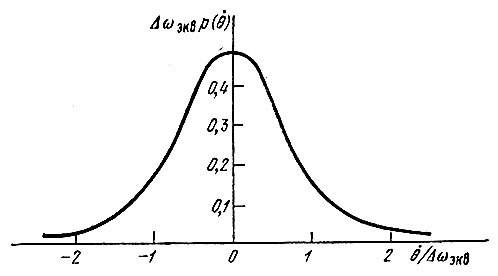
Рис. 4.18. Плотность вероятности производной фазы нормального случайного процесса
Рассмотрим в качестве примера случай, когда энергетический спектр W(ω) равномерен в полосе частот ±Δω при центральной частоте ω0.
Нормированная корреляционная функция в соответствии с выражением (4.44)
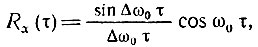
а
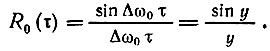
Дважды дифференцируя последнее выражение по τ, находим
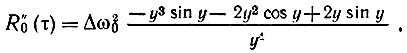
При 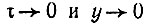 получаем
получаем
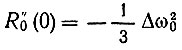
и
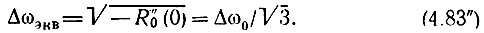
Итак, в случае шума с энергетическим спектром, равномерным в полосе (-Δω0, Δω0) (см. рис. 4.9), среднее значение величины 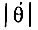 равно
равно 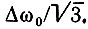

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
